|
▲ Выше
▼ Пишут о ПИОНЕРе
▼ Мансуров
▼ Линдер
▼ Штильман
|
|
По стопам ПИОНЕРа |
|
Контроверза Модель игры Хронология модели От ПИОНЕРа к Лингвистической Геометрии Тесты для шахматной LG-системы О языке программирования LG-систем |
|
"И не одно сокровище, быть может, минуя внуков, к правнукам уйдёт..."
Осип Мандельштам
|
|
Контроверза |
|
"Мы ленивы и не любопытны"
Александр Пушкин
|
|
Сегодня программирование шахмат — это задача для школьника или студента и новой играющей программой трудно кого-то удивить. Однако, в прошлые 60-е — 70-е годы, когда компьютеры были слабые и малодоступные, это "развлечение" могли себе позволить только программисты оборонных НИИ, где были лучшие ЭВМ. А чтобы как-то оправдать расход машинного времени дорогих ЭВМ, нужно было обязательно поупражняться в философии, типа: мол, искусственный интеллект (ИИ) приведёт к прогрессу в планировании и управлении, а логические игры ума — это пробный камень для реальных систем ИИ, поэтому создание сильной шахматной программы — серьёзное дело для учёных мужей. Но этих доводов всё же не хватало для официального финансирования, и шахматные программы делались факультативно (Донской, "Каисса"). Больше всех и в печати, и в высоких кабинетах доказывать важность компьютерного моделирования шахматной игры пришлось Ботвиннику (1961, 1987, 1997), который стремился открыто и профессионально заниматься программированием шахмат и единственный в СССР, кто этого добился — проекты ПИОНЕР [1958-1990], (Ботвинник, 1968, 1975, 1979, 1989) и CC Sapiens [1990-1995], (Е.Мансуров, 2004). Однако к тому моменту, когда Ботвинник (1987e, 1997), впервые (1964) написал о своих идеях создания компьютерного гроссмейстера президенту АН СССР и сделал своё конкретное предложение, работа над первой советской шахматной программой уже велась (неофициально) в ИТЭФ под руководством Адельсона-Вельского. В 1966-67 году эта программа со счетом 3:1 выиграла матч "по переписке" у американской программы Котока и Маккарти из университета в Стэнфорде (США, Калифорния), (Ботвинник, 1968; Донской, "Каисса"). С этого момента началось великое противостояние двух направлений в моделировании шахмат, которое не закончилось и по сей день (Е.Мансуров, 2004).
Известно, что при моделированиии разумного поведения эксперта при решении
сложных задач можно применять
два
подхода
(К.Шеннон,
1950):
Если научную задачу нужно решить хоть как-нибудь, то 1-й подход годится всегда! Поэтому на первых порах полный перебор, метко названный американцами "брут форс" (brute force — грубая сила) использовали все, кто программировал шахматную игру (кроме Ботвинника). Со временем необходимость оправдываться, что, дескать, программирование шахмат приведёт к прогрессу в управлении, как-то утратило свою актуальность. В 80-х годах у науки на западе появилась другая, но вполне конкретная коммерческая цель — создавать компьютерные программы для соревнования с человеком-гроссмейстером (в целях их рекламной "раскрутки"), чтобы потом эти раскрученные программы для ПК и бытовые шахматные автоматы продавать на рынке. Теория программирования шахмат стала коммерческой тайной (Е.Мансуров, 2004). В СССР такого рынка не было, а компьютеры заметно отставали от западных. К тому же советская программа "Каисса" (победитель 1-го чемпионата мира среди шахматных программ в 1974 году) даже на мощном американском компьютере в чемпионате 1980 года показала только четвёртый результат. В чемпионатах шахматных программ "Каисса" больше не участвовала, хотя её авторы ещё продолжали заниматься программированием концов шахматной игры (Карпов и Гик, 1984, 1991, 1991a; Адельсон-Вельский и др., 1983). В центральных СМИ о "Каиссе" перестали упоминать. Революция в области электроники в 90-х годах и возрастание мощи компьютеров (по скорости процессоров и размерам оперативной памяти) позволили шахматным программам на западе повысить свой уровень игры до гроссмейстера. Сегодня обилие шахматных программ (движков) с разнообразными шахматными досками и с разной силой игры просто поражает (сайты: 2001, 2004). Видимо, жажда проверить на шахматах "мускулы" своего ума у программистов всего мира не угасает, хотя их энергия достойна применения в иных, как говорится, "мирных целях". Ведь использование таких шахматных программ (и коллекций их алгоритмов) в других прикладных областях, где встречаются похожие переборные задачи, может быть весьма трудным делом (Stilman, 2000). В свете выше сказанного, все укоры Ботвиннику в том, что он якобы пытался запрограммировать только себя, т.е. своё видение шахмат, и поэтому его модель шахматной игры ограничена и не отражает всего многообразия взглядов на шахматы (интуиция человека, фантазия и пр.), сегодня (как, впрочем, и тогда) выглядят просто нелепо. (Возможно, что так, ну и что?). Точно так же, как и фразы, что, дескать, программировать шахматы должны “математики, а не профаны”, т.е. не доктор электротехники, хотя и экс-чемпион мира по шахматам — будто бы сам Ботвинник собирался писать программы на ФОРТРАНе, и будто бы в его лаборатории не было профессиональных математиков-программистов (Мирный В.Р. и др., 1986; Мирный В.Р., Чудаков М.В., Штильман Б.М., 1988; Stilman B., 1994f, 2000). Подобные "уколы" в адрес Ботвинника можно встретить на русском и английском языке в интернете, стоит лишь ввести в строке поиска фразу "ПИОНЕР & Ботвинник" или "PIONEER & Botvinnik" (Мансуров, 2004). Видимо, господа профессиональные математики пока ещё не преодолели "силу притяжения" 1-го подхода к решению переборных задач и поэтому считают, что другого подхода просто нет в природе. NB. А истина лежит посередине — без перебора всё-таки не обойтись (Stilman, 2000; Кронрод, 2004), но вопрос в том, из каких возможностей выбирать? Если оставаться в исходном пространстве и перебирать в каждом узле дерева все возможные ходы всех фигур, то это — "брут форс", где нет понимания позиции, нет и ассоциаций с опытом прошлого. Если же перейти в другое пространство разумных (нацеленных) ходов или планов (стратегий), то перебор будет вполне уместен, т.к. понимание позиции в виде набора возможных (присутствующих) стратегий игры достигнуто. Дело за малым — как это всё формализовать? Применение 2-го подхода зачастую дело трудное, т.к. требует формализации знаний эксперта, а “алгоритм гроссмейстера лежит за семью печатями” (Ботвинник, 1989) и полностью “пока ещё не раскрыт” (Stilman, 2000), т.е. не известен в точности науке. |
|
Модель игры |
|
"Никто не обнимет необъятного"
Козьма Прутков
"Мысли и афоризмы",3,44. |
|
Ботвинник работал над созданием компьютерного гроссмейстера с 1958 по 1995 годы (Stilman, 2000; Мансуров, 2004). Он поставил перед собой максимальную, фантастическую задачу — сделать программу для компьютера, которая бы играла в шахматы как человек, т.е. не перебирала все возможные ходы в позиции, а находила лучший ход и строила понятное человеку дерево вариантов, т.е. “узкое и глубокое дерево перебора”. Начав с размышлений над алгоритмом поиска хода (в шахматной позиции), который выработали люди-мастера за 5 столетий существования современных шахмат, Ботвинник (1987e), наконец, пришёл к идее неточной цели в шахматной игре (это борьба за материал), т.к. точная цель (по правилам шахмат — это мат королю) могла быть сразу и не достижима. Дело в том, что поиск лучшего хода в шахматной позиции — это задача с деревом перебора гигантского размера, и поэтому она не всегда может быть решена точно, в смысле перебора абсолютно всех вариантов. Значит шахматы — скорее задача, которая не решается точно, т.е. не точно решаемая или неточная. Подтверждение своей идее (что в гроссмейстерских шахматах главное — борьба за материал) Ботвинник нашёл у Капабланки, в предисловии к его учебнику шахмат (Ботвинник, 1975, 1987f, 2000). Оттолкнувшись от этого принципа — “примата нападения” (т.е. атаки) — и, ориентируясь на стремление фигур одной армии нападать на фигуры другой армии, Ботвинник придумал траектории движения атакующих фигур в горизонте видимости мишеней (в шахматных полуходах) и зоны, как группы фигур, препятствующих (т.е. отрицающих со знаком "-") и поддерживающих (т.е. отрицающих со знаком "+" траектории отрицаний со знаком "-") атакующую фигуру — комль зоны игры (Ботвинник, ПИОНЕР). Получилась модель шахматной игры по Ботвиннику (1968, 1975, 1979, 1989). Почему-то критики (шахматисты и математики) решили, что по такой же схеме за шахматной доской думает и сам Ботвинник? (Бронштейн, 2003 — но здесь скорее личная антипатия к Ботвиннику (Харитон, 2001, 2003), чем объективность изумительного шахматного писателя Давида Бронштейна !) Любую позицию можно рассматривать как совокупность зон, позже названных цепочками фигур, (Ботвинник, 1989). Перебор ходов фигур по траекториям в зонах приводит к построению дерева перебора, которое выглядит вполне разумным и допускает стандартные обрезания (т.е. различные отсечения) ветвей. Чтобы уменьшить и это не слишком большое дерево, используется система приоритетов — в какой зоне начинать движение фигур. NB. Пожалуй, эти приоритеты оказались камнем преткновения всей модели, т.к. Ботвинник стремился во что бы то ни стало получать "человеческие" деревья перебора, а для этого нужно было уметь находить лучший ход в пространстве траекторий. Это долго не удавалось, т.к. в сложных позициях (с многочисленными зонами) выбор приоритетного хода люди делают "по позиции", т.е. по опыту и интуиции. Значит, лучший ход — это не примитивное нападение, а ход, приводящий в позицию с более высокой обобщённой оценкой. Обобщённая оценка позиции складывается из обычной материальной стоимости фигур плюс "невидимые" стоимости (“конъюнктурные” — Ботвинник, 1968; или “ситуационные” (“situational values”) — Stilman, 2000), как надежды на возрастание обычной стоимости фигуры в результате предстоящего взятия ею фигуры противника или возможного превращения (если она — пешка) в старшую фигуру (ферзя), т.е. в результате “обобщённого размена” (Ботвинник, 1987b). Алгоритмы вычисления "невидимых" стоимостей фигур для выбора лучшего (приоритетного) хода многократно перестраивались (Ботвинник, 1968, 1980a, 1987ee, 1989), но так и не были доведены до завершения (Ботвинник, 1997; Линдер В. и Линдер И., 2001). Поэтому ПИОНЕРу лучше удавались решения сложных позиций с этюдной атакой (скрытой комбинацией) на большую глубину, чем спокойные или закрытые сложные позиции, в которых люди просто маневрируют или делают профилактические ходы (Ботвинник, 1989; Адельсон-Вельский и др., 1983). Пространство траекторий оказалось похожим на Web-сеть, потому что "кирпичики" модели — поля траекторий, сами траектории, пучки траекторий от начального Ao-поля и до конечного Ak-поля, зоны (как совокупности пучков отрицания вместе с пучками отступления мишени и пучком нападения комля) и, собственно, перебор ходов в совокупности зон — связаны между собой в многоуровневую иерархию, чем-то мне напоминающую русскую матрёшку (т.е. куколки от мала до велика, вложенные одна в другую). Действительно, траектория — это цепочка полей, пучок — это цепочка траекторий (точнее гамак-граф полей с Ao и Ak точками крепления), зона — это цепочка пучков траекторий (или сеть траекторий), сложная зона (совокупность связанных зон) — это цепочка простых зон, дерево перебора — это цепочка ходов фигур по траекториям (вместе с методами формирования дерева: обрыв ветви-варианта, минимакс оценок на подъёме, отсечения ветвей на подъёме и при спуске и пр.). Однако, понятие цепочки символов — фундаментально для математической лингвистики, в которой грамматики занимаются порождением цепочек, т.е. слов формальных языков. Оказалось, что лингвистическая интерпретация наиболее адекватно отображает поведение модели игры (Штильман, 1981, 1985b). Но в формальные языки из цепочек затесались геометрические структуры — карты полей шахматной доски 8х8 с возможными ходами фигур. А что, если доска будет трёхмерной (50х50х10) и фигуры не шахматные, а — роботы (т.е. самолёты, автомобили и пр.)? Учитывая геометрические мотивы пространства траекторий, математики из лаборатории Ботвинника окрестили подобный подход к моделированию переборных задач Лингвистической Геометрией (LG), (Stilman, 2000). Однако, сам Ботвинник называл этот подход по разному — "АЛГОРИТМ БОТВИННИКА" (1975), "метод ПИОНЕРа" (1977-1987), а позже "Шахматным методом решения переборных задач" (1987ee, 1989). Укрупняя, можно считать, что в модели игры на доске имеются три уровня (ступени) иерархии формальных языков:
* семейство языков Траекторий — путей для передвижения фигур;
т.е. переборы ходов или
“виртуальные розыгрыши” позиции, приводящие к построению LG-дерева
(Stilman,
2000).
* семейство языков Сетей Траекторий (включая язык Зон); * семейство языков Переводов состояний Сложной Системы в LG-дерево, На каждом уровне работает своя цель, но в итоге всё сводится к главной (неточной) цели игры — выигрышу материала (в смысле обобщённой стоимости). Ботвинник называл это трехступенчатой системой управления, хотя "три" может превращаться и в большие числа. |
|
Хронология модели |
| "История — ключ к пониманию современности" |
|
1949. Доклады Клода Шеннона о шахматной программе для компьютера (1950). |
|
От границы мы Землю вертели назад — было дело сначала, — но обратно её закрутил наш комбат, оттолкнувшись ногой от Урала.
Владимир Высоцкий
"Мы вращаем землю", 1972.
|
| 1958.
Идея Ботвинника сделать компьютерного гроссмейстера.
"Энциклопедия шахмат", раздел "Ботвинник"
из главы 1. АЛГОРИТМ МАСТЕРА |
| 1960.
Лекция Ботвинника перед журналистами в Берлине, в Университете им. Гумбольдта:
"Люди и машины за шахматной доской". |
| 1961.
Статья: Ботвинник М.М., "Люди и машины за шахматной доской",
Шахматы в СССР, 1961, № 3, Москва, см. также Ботвинник М.М., 1987, ПИОНЕР). |
| 1964.
Цель шахматной игры
(Ботвинник,
ПИОНЕР;
Мансуров,
2004).
"...нашел цель неточной игры в шахматы"
Из гл. "К достижению цели. Алгоритм игры в шахматы" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987e, с.483-484. |
| 1966.
Диспут в ЦШК.
Траектории фигур. Таблицы 15х15. Володя Бутенко программирует траектории шахматных фигур. |
| 1968.
Книга: Ботвинник М.М., Алгоритм игры в шахматы, "Наука", Москва, 1968
Конъюнктурные стоимости фигур.
"процесс шахматной игры... состоит в обобщённом размене"
Из кн. Ботвинник, "Алгоритм игры в шахматы", 1968, с.29-30. |
| 1969. Зона шахматной игры. |
| 1970.
Книга: Botvinnik, M.M., "Chess, Computers and Long-Range Planning", Springer-Verlag, Berlin,
Heidelberg, and New York, 1970, (перевод с русского Ботвинник М.М., 1968 на английский). Отказ Бутенко сотрудничать с Ботвинником.
"Бутенко решил, что включение зоны в алгоритм необязательно."
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.503-504. Ботвинник принимает решение отказаться от участия в шахматных турнирах. Остаются — электротехника и шахматная программа. |
|
Наконец-то нам дали приказ наступать, отбирать наши пяди и крохи, — но мы помним, как солнце отправилось вспять и едва не зашло на Востоке.
Владимир Высоцкий
"Мы вращаем землю", 1972.
|
| 1972.
Препринт: Ботвинник М.М., "Блок-схема алгоритма игры в шахматы", АН СССР:
Научная секция по комплексной проблеме "Кибернетика", Москва, 1972, 28 стр. (Stilman, 2000) В лаборатории Ботвинника в ВНИИЭ открыта научная тема по шахматной программе. Программисты Борис Штильман и Александр Юдин. (Stilman, 2000) Компьютерное время на английской ЭВМ ICL 4-70 (клон IBM/360).
"Б.Штильман работал со всей энергией."
Из Приложения 2 "Как создавался шахматный метод" в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.100. |
| 1973.
Препринт: Ботвинник М.М., "О кибернетической цели шахматной игры", АН СССР:
Научная секция по комплексной проблеме "Кибернетика", Москва, 1973, 40 стр. |
| 1974.
Ботвинник принимает решение отказаться от электротехники
и заниматься только шахматной программой. |
| 1975.
Книга: Ботвинник М.М., О кибернетической цели игры, "Советское радио", Москва, 1975
Штильман Б.М., "Формирование множества пучков траекторий", Приложение 1, стр.70-78 в кн. Ботвинник М.М., 1975.
"материал и контроль полей"
Из "Послесловия" в кн. Ботвинник, "О кибернетической цели игры", 1975, с.68. Botvinnik, M.M., Stilman, B., Yudin, A.D., Lozinskiy, D.N., Poltavets, L.M., Research of Possibilities for Program Design on the Basis of the BOTVINNIK ALGORITHM for Solving Economic Problems, Report No. 12-0113/72, National Research Inst. for Electrical Engineering, Moscow, Russia, 78 pp., 1975. (Ботвинник M.M., Штильман Б., Юдин А., Лозинский Д.Н., Полтавец Л.М., "Исследование возможности применения проекта программы на основе АЛГОРИТМА БОТВИННИКа для решения экономических задач", Отчет №12-0113/72, ВНИИЭ, Москва, Россия, 78 стр., 1975.) |
| 1976.
Штильман Б.М., "О программе формирования зоны игры", Деп. ВИНИТИ 3947-76, (тоже в
Штильман Б.М., 1979). Штильман Б.М. "Дерево перебора в зоне игры", Деп. ВИНИТИ 3947а-76, (тоже в Штильман Б.М., 1979). Приглашение на второй чемпионат мира шахматных программ в Торонто, Канада. |
|
И от ветра с Востока пригнулись стога, жмётся к скалам отара. Ось земную мы сдвинули без рычага, изменив направленье удара.
Владимир Высоцкий
"Мы вращаем землю", 1972.
|
| 1977.
Решение этюда Р.Рети. ( 28 января 1977 )
Решение этюда Ботвинника и Каминера. ( 11 апреля 1977 ) Решение этюда Г.Надареишвили. ( 3 августа 1977 ) Шахматную программу окрестили ПИОНЕРом.
"...пришлось программу "крестить"."
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.512. Грант на компьютерное время: — from the National Scientific Information Center for the development of the PIONEER project (for 1 year, computer time on Burroughs B-6700), USSR. Новые программисты — Александр Резницкий и Михаил Цфасман. |
|
Животом - по грязи, дышим смрадом болот, но глаза закрываем на запах. Нынче по небу солнце нормально идёт, потому что мы рвёмся на Запад!
Владимир Высоцкий
"Мы вращаем землю", 1972.
|
| 1978.
Ботвинник М.М., Штильман Б.М., Юдин А.Д. "Искусственный шахматный мастер",
Вестник АН СССР, Москва, 1978, № 4, стр.82-91. "1-я диссертация" Штильмана ("волшебная сказка" программиста): Штильман Б.М. "Исследование системы управления на основе модели шахматной игры", Технический отчёт, ВНИИЭ, Москва, 1978, 201 стр. Гранты на компьютерное время: — from the University of Mannheim for the improvement and completion of the PIONEER project (for 0.5 year), Germany. — from the University of Dortmund for the development of AI theory of complex systems and its application to the PIONEER project (for 0.5 year), Germany. — from Control Data Corp.(CDC) for the improvement of the PIONEER program and development of efficient methods for solving practical search problems (for 0.5 year), USA. |
| 1979.
Совещание по поводу выезда программистов Ботвинника за рубеж — 9 февраля 1979.
(Донской, "Крупные фигуры"). Решение позиции из партии Ботвинник—Капабланка, АВРО-турнир, 1938 ( 5 июля 1979 ). Выступления в городах СССР с рассказом о ПИОНЕРе (поиск ученого совета для защиты). "Шахматы — не предмет науки" ?! (Stilman, 2000) Книга: Ботвинник М.М., О решении неточных переборных задач, "Советское радио", Москва, 1979 |
|
Кто-то встал в полный рост и, отвесив поклон, принял пулю на вдохе, но на Запад, на Запад ползёт батальон, чтобы солнце взошло на Востоке.
Владимир Высоцкий
"Мы вращаем землю", 1972.
|
| 1980.
Ботвинник М.М., Штильман Б.М., Юдин А.Д., Резницкий А.И., Цфасман М.А.,
"О шахматистах и компьютерах", Препринт для 2-го Международного симпозиума по Искусственному Интеллекту, 9 стр., Репино, Ленинград, Россия, октябрь 1980. Уволился программист — Александр Юдин.
"Но как эти конъюнктурные стоимости формализовать и вычислять?"
Из ст. "Методом "божьей коровки"" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987, с.246-247. Планирование ремонтов на электростанциях. Stilman, B., Reznitskiy, A.I., Design of New Method for Solving Complex Search Problems and its Application to Power Control, Report awarded at the Moscow Young Scientists Contest, Moscow, Russia, 30 pp., 1981. (Штильман Б.М., Резницкий А.И., "Проект нового метода для решения сложных переборных задач и его применение к управлению электроэнергетикой", Сообщение, предоставленное на конкурс молодых московских ученых, Москва, Россия, 30 стр, 1981.) NATIONAL YOUNG INVESTIGATOR AWARD from the USSR Academy of Sciences (B.Stilman, A.Reznitskiy) for the development of new approach for solving Artificial Intelligence problems and its application to power control, USSR. (Премия от Академии Наук СССР (Штильман Б., Резницкий А.), "за развитие нового подхода для решения задач Искусственного Интеллекта и его применение к управлению электроэнергетикой", СССР.) Новый программист — Вадим Мирный (Stilman, 2000). 
Москва, 1980. Слева направо: Резницкий, Штильман, Донской, Ботвинник и Ньюборн |
| 1981.
Нет современного компьютера.
Выступление в Ленинграде с рассказом о ПИОНЕРе (поиск ученого совета для защиты). Уволился программист — Михаил Цфасман. "Зачем ЭВМ играет в шахматы", газета "Правда", Март 30, 1981, Москва, (см. также Ботвинник М.М., 1987). "2-я диссертация" Штильмана (рождение Лингвистической Геометрии): Штильман Б.М. "Иерархия формальных грамматик для решения переборных задач", Технический отчёт, ВНИИЭ, Москва, 1981, 105 стр.
"зона игры была превращена в цепочку фигур"
Из кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.15. Botvinnik, M.M., Stilman, B., Reznitskiy, A.I., Solving of Problem of Planning Maintenance Work for Power Station Equipment on the basis of PIONEER Method, Report No. 16-0200/79, National Research Inst. for Electrical Engineering, Moscow, Russia, 82 pp., 1981. (Ботвинник M.M., Штильман Б., Резницкий А.И., "Решение задачи планирования работы по ремонту оборудования электростанции на основе метода ПИОНЕР", Отчет №16-0200/79, ВНИИЭ, Москва, Россия, 82 стр, 1981.) Новый программист — Михаил Чудаков. |
| 1982.
Есть современный компьютер!
"К тому времени мы уже перестали бедствовать с машинным временем."
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.519-520. Грант на компьютерное время (600 тыс. руб): — from the USSR National Committee for Science and Technology for the design of new methods and software for solving complex search problems, (for 3 years, M.Botvinnik, B.Stilman, V.Mirniy, A.Reznitskiy), USSR. Книга: Botvinnik, M.M., "Meine neuen Ideen zur Shachprogrammierung", Springer-Verlag, Berlin, Heidelberg, and New York, 177 pp., 1982, (перевод Ботвинник M.M., 1979 на немецкий).
"Б.Штильман "покатил налево""
Из Приложения 2 "Как создавался шахматный метод" в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.103. |
| 1983.
Ботвинник М.М., Петряев Е., Резницкий А.И., Сюткин Б.Д., Тимофеев Я.И., Уланов Г.А.,
"Применение нового метода решения переборных задач к планирования ремонтов оборудования электростанций", Экономика и математические методы, Москва, 1983, т.19, вып.6, стр.1030-1041, (см. также Ботвинник М.М., 1989). Резницкий А.И., Штильман Б.М. "Применение метода ПИОНЕР в планировании ремонтов энергооборудования", Автоматика и телемеханика, 1983, № 11, с.147-153. Ботвинник М.М., Мирный В.Р. "Алгоритм выравнивания графика нагрузки энергосистем", рабочие заметки. 
New York, 1983. WCCC-4. Слева направо: Beal, Thompson, Newborn, Botvinnik 
New York, 1983. WCCC-4. Слева направо: Thompson, Botvinnik. |
| 1984.
Книга: Botvinnik, M.M., "Computers in Chess: Solving inexact search problems",
Springer Series in Symbolic Computation, with Appendixes, Springer-Verlag, New York, 158 pp., 1984, (перевод Ботвинник M.M., 1979 на английский). Защиты кандидатских диссертаций Резницого и Штильмана. (Донской, "Крупные фигуры").
"В декабре 1984 года защиты состоялись."
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.519-520. Штильман Б.М. "Разработка метода иерархии формальных грамматик и его применение в планировании ремонтов энергооборудования", Тезисы диссертации к.т.н., ВНИИЭ, Москва, 1984, 182 стр. |
| 1985.
Грант на компьютерное время (600 тыс. руб):
— from the USSR National Committee for Science and Technology and Department of Energy for the development of AI methods and software tools for solving long-range planning problems (for 3 years, M. Botvinnik, B.Stilman, V. Mirniy, A. Reznitskiy),USSR. Штильман Б.М. "Иерархия формальных грамматик для решения переборных задач", Искусственный интеллект. Итоги и перспективы. Труды международной рабочей группы, Москва, 1985, стр.63-72. Штильман Б.М. "Формально-лингвистическая модель для решения задач дискретной оптимизации. 1. Инструментарий формализации. Язык траекторий", Известия АН СССР. Техническая кибернетика, Москва, 1985, № 3, стр.110-122, 4886 экз. Штильман Б.М. "Формально-лингвистическая модель для решения задач дискретной оптимизации. 2. Язык зон, переводы и проблема границ", Известия АН СССР. Техническая кибернетика, Москва, 1985, № 4, стр.10-21, 4886 экз. |
|
Здесь никто не найдет, даже если б хотел, руки кверху поднявших. Всем живым — ощутимая польза от тел: как прикрытье используем павших. Этот глупый свинец всех ли сразу найдёт, где настигнет — в упор или с тыла? Кто-то там впереди навалился на дот — и Земля на мгновенье застыла.
Владимир Высоцкий
"Мы вращаем землю", 1972.
|
| 1986.
Мирный В.Р., Ройзнер А.Г., Чудаков М.В., Штильман Б.М., "Инструментальная
система поддержки разработки и отладки больших программ на ФОРТРАНе ЕС ЭВМ", Программирование, Москва, 1986, № 5, стр.27-38. |
| 1987.
Книга: Ботвинник М.М., Аналитические и критические работы 1928-1986:
Статьи, воспоминания, 4-й том, "Физкультура и спорт", Москва, 1987, 528 стр. Botvinnik, M.M., Stilman, B., Mirniy, V.R., Reznitskiy, A.I., Chudakov, M.V., Improvement and Application of PIONEER for Solving Search Problems, Report No. 1601/85, National Research Inst. for Electrical Engineering, Moscow, Russia, 52 pp., 1987. (Ботвинник M.M., Штильман Б., Mirniy В.Р., Резницкий А.И., Чудаков М., "Усовершенствование и применение ПИОНЕРа для решения переборных задач", Отчет №1601/85, ВНИИЭ, Москвы, России, 52 стр, 1987.)
"А как же с шахматной программой ?"
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.521.
"...потребует новой подпрограммы составления цепочек"
Из кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.27. |
| 1988.
Мирный В.Р., Чудаков М.В., Штильман Б.М.
"АРМ программиста на основе интегрированной системы версий программ", Программная инженерия, МДНТП им.Дзержинского, Москва, 1988, стр.59-65, (Stilman B., 1994f, 2000). Уволились программисты — Вадим Мирный и Борис Штильман.
Из выступления Михаила Ботвинника
на семинаре по вопросам шахматной программы ПИОНЕР и современным персональным компьютерам, Москва, СССР, 1988 г. (Мансуров, 2004). |
| 1989.
Книга: Ботвинник М.М., Шахматный метод решения переборных задач, "Советский спорт",
Москва, 1989
"...надо было сделать более экономный и близкий алгоритму мастера вариант программы..."
Из Приложения 2 "Как создавался шахматный метод" в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.104. |
| 1990.
Уволились программисты — Александр Резницкий и Михаил Чудаков.
Закончился проект ПИОНЕР. |
|
За нашей спиною в шесть тридцать остались — я знаю,— Не только паденья, закаты, но взлёт и Восход. Два провода голых, зубами скрипя, зачищаю, — Восхода не видел, но понял: вот-вот — и взойдёт. ...Уходит обратно на нас поредевшая рота. Что было — не важно, а важен лишь взорваный форт. Мне хочется верить, что грубая наша работа Вам дарит возможность беспошлинно видеть Восход.
Владимир Высоцкий
"Черные бушлаты", 1972.
|
| 1990-1994.
Программа "с нуля". Проект "СНЕSS COMPUTER SAPIENS".
Современные компьютеры — рабочие станции (workstation) корпорации Hewlett-Packard. Новая команда программистов. (Мансуров, 2004). |
| 1995. Уход Ботвинника. (Мансуров, 2004) |
| 1997. Книга воспоминаний: Ботвинник М.М., У цели, Москва, 1997. |
| 2000.
Штильман Борис, "Лингвистическая Геометрия: от Перебора к Построению",
Stilman Boris (2000), "Linguistic Geometry: From Search to Construction", Series: Operations Research/Computer Science Interfaces Series, Vol. 13, 2000, 416p., Hardcover, ISBN: 0-7923-7738-9, © Springer. Part of Springer Science+Business Media |
2000-2010.

2007. док. Борис Штильман 
2007. док. Борис Штильман 
2010. док. Борис Штильман |
|
От ПИОНЕРа к Лингвистической Геометрии |
|
"... Когда великий Глюк явился и открыл нам новы тайны (глубокие, пленительные тайны !), не бросил ли я всё, что прежде знал, что так любил, чему так жарко верил, и не пошёл ли бодро вслед за ним безропотно, как тот, кто заблуждался и встречным послан в сторону иную."
Александр Пушкин
"Моцарт и Сальери", 1830. |
|
Проект ПИОНЕР закончился в конце 80-х годов одновременно с выходом последней научной книги Ботвинника (1989) о программировании шахмат, которую отделяло от предыдущей (1979) целых десять лет. Подводя итог этим исследованиям, Штильман (2000) пишет:
"Проект ПИОНЕР закончился разработкой одной из самых интересных и мощных эвристических моделей, основанной на эвристических сетях. Применение разработанной модели к шахматной игре было полностью реализовано в виде программы ПИОНЕР 1.x... Аналогичная эвристическая модель была также реализована для долгосрочного календарного планирования в виде набора программ ПИОНЕР 2.x, 3.x, 4.x. Они использовались для составления графика ремонтов электроагрегатов, для сглаживания графика потребления мощности и для планирования народного хозяйства в прежнем СССР... Эти модели... были представлены в форме идей, правдоподобных рассуждений и работающих программ."
Время ускоряло бег. На смену большим ЭВМ пришли персональные компьютеры, постепенно ставшие доступными широкой публике. В 1997 году компьютерная система Deep Blue фирмы IBM выиграла матч у чемпиона мира Гарри Каспарова (Е.Мансуров, 2004, ч.9,10). С точки зрения сторонников 1-го подхода ("брут форс") шахматы перестали быть "дрозофилой" ИИ (Донской, "Каисса"; Донской и Битман, 2002). Однако, это было совсем не то, к чему стремился Ботвинник. О роли шахмат в ИИ Штильман (2000) пишет так:
"Когда работа над этой книгой была почти закончена, я узнал о следующем заявлении профессора Джона Маккарти (John McCarthy) из Стэнфордского Университета. В своих комментариях о решении шахматного
этюда Рети
компьютерами он писал: “Обратите внимание, что идея Рети может быть реализована на доске размером 100x100, и люди всё ещё смогут решать эту задачу, но современные программы [традиционные, т.е. работающие по методу "брут форс" — Б.Ш.] уже не смогут... Шахматы по-прежнему будут служить дрозофилой для ИИ, если исследователи попробуют создать программу, которая сможет решать задачи на доске произвольного размера. Однако, ИИ не будет продвигаться к человеческому уровню, если исследователи ИИ удовлетворятся методом "брут форс" как заменой интеллекта... Будет ли кто-нибудь серьёзно утверждать, что компьютер не сможет решить этюд Рети методом, отличным от "брут форс"?” (Маккарти,1998). Конечно, LG была разработана независимо и за длительный период времени. Однако, удивительно, что исследования по LG вдохновлялись аналогичными идеями."
С другой стороны, становление Лингвистической Геометрии в 90-х годах, как самостоятельной математической дисциплины, снимает с шахмат "ореол" исключительности — быть единственной "дрозофилой" ИИ, (Stilman, 2000). К тому же, длительный опыт программирования показал, что шахматная игра неудобна для математического моделирования из-за большой “ничейной зоны” (Битман), т.е. “область экстремума (победы) не допускает постепенного приближения (по градиенту)” (Штильман), или иначе область экстремума — не холм, а похожа скорее на дельта-функцию, т.к. зачастую только одна ветвь LG-дерева ведёт к победе, а остальные — к ничьей или к поражению, (Stilman, 2000). Сегодня интересны приложения LG к робототехнике (Алферов Г.В., 1998), к системам реального времени (реакция LG-систем практически мгновенна, потому что они не перебирают всё подряд), к созданию беспилотных транспортных средств, а так же к тем наукоёмким областям, где имеется сложный перебор, возможно, что это — генетика, фармацевтика, информатика и пр. (Stilman, 2000). Неудача Ботвинника (в создании играющей шахматной программы), который упорно искал алгоритм выбора лучшего хода в любой позиции (такого хода, какой сделают люди-гроссмейстеры), привела к пониманию неимоверной сложность такой постановки задачи, т.е. задачи построения человеческого дерева перебора для любой шахматной позиции (Линдер В. и Линдер И., 2001 ). Этого не хотят понимать сторонники подхода "брут форс" (Донской, "Крупные фигуры"; Мансуров, 2004). Проект ПИОНЕР (как LG-подход к шахматам) показал, что обучение прототипа шахматной LG-системы умению разыгрывать некоторые шахматные позиции (не говоря уже о любых) может быть очень сложным, и что такие исследования могут растянуться на годы. Так что шахматной программы по Ботвиннику пока нет. Видимо сложность моделирования шахмат в проекте ПИОНЕР привела к такому высказыванию математика Штильмана: "Шахматы являются скорее скорлупой, которая закрывает ядро — LG-подход", отвлекая исследователей от успешного применения его в других прикладных областях, где нет таких, специфичных только для шахмат, особенностей, как блокада фигурой противника траектории атаки (т.е. не нужная жертва, лишь задерживающая на один ход продвижение стрелка к мишени, если она бессмысленна и не спасает ситуацию — то, что Ганс Берлинер назвал в своей диссертации 1974 года "эффектом горизонта", т.е. перенос неизбежной потери особо ценной мишени за горизонт, за предельную длину вариантов перебора (Лорьер, 1991)), взятие пешкой "на проходе"; рокировка и прочее. Конечно, для любителей шахматного программирования такое замечание может показаться неприятным и горьким, но так оно и есть. Известно, что дорогостоящие научно-исследовательские проекты, как правило, рано или поздно заканчиваются ожидаемыми результатами, например Дип Блю (Deep Blue, IBM), победившая Каспарова. Заказчик какое-то время терпит отсутствие результата, соглашаяся с неизбежными трудностями, встающими перед исследователями, но потом требует результат во чтобы-то ни стало (любой ценой). Как следствие, в 80% проектов результаты "натянуты", т.е. не совсем достоверны, т.к. не все проблемы удалось решить. Лишь мизерная часть проектов приводит не к ожидаемым, а к неожиданным результатам (по принципу — новое знание только расширяет границы нашего незнания или, как говорили древние, "во многой мудрости много печали"). Может быть к таким проектам относится и ПИОНЕР в смысле "главной" цели — создание шахматной программы, которая строит дерево как человек-гроссмейстер. Хотя, как научный проект, ПИОНЕР выглядел вполне достойно и даже можно считать его успешным. Однако, тем неожидаемым результатом (с точки зрения Ботвинника) оказалась Лингвистическая Геометрия, которую правильнее (и проще для нас) связывать с именем Бориса Штильмана, хотя он не забывает отметить, что в создание LG-подхода к решению сложных переборных задач были вовлечены многие научные сотрудники (участники проекта ПИОНЕР), крупные учёные и финансовые организации (Stilman, 2000). Всё же, пока не создан программный мастер (wizard), который бы генерировал прототипы LG-систем для разных прикладных областей, создавать LG-системы в этих областях без эксперта-человека затруднительно. Поэтому шахматы всё ещё остаются той областью, для которой прототипы LG-систем создавать можно, т.к. люди-эксперты, понимающие эту игру, есть (Stilman, 2000). |
|
Тесты для шахматной LG-системы |
|
"Отыщи всему начало, и ты многое поймёшь"
Козьма Прутков
"Мысли и афоризмы-2", 92. |
|
Программы — прототипы LG-систем — очень сложны в отладке, т.к. сама модель является сложной, особенно когда ещё не всё себе представляешь. Кроме того, приходиться тестировать много разных алгоритмов сокращения дерева перебора. Поэтому для прототипов LG-систем необходимо иметь классы тестов возрастающей трудности. Классификацию сложных тестов приводит (Stilman, 2000). Однако в самом начале разработки программных LG-систем нужно располагать примитивными тестами. Опять же Штильман, ещё в препринте (1976aa) рассматривал простую позицию (искусственного) шахматного эндшпиля для иллюстрации работы программы ПИОНЕР при формировании зоны.
Рис.1 "00_NhPfBg"-тест LG-системы
LG-анализ подобных позиций показывает, что они состоят из одной-двух зон, а пучок нападения комлевой фигуры имеет одну-две траектории. По аналогии с той позицией, я построил набор тестовых позиций, которые называю вариациями "0-теста Б.Штильмана" для прототипа своей шахматной LG-системы. Основными источниками, содержащими формализацию алгоритмов и блок-схемы, которые я использовал для программирования, были, написанные Штильманом, приложения в книгах Ботвинника (1975, 1979) плюс здравый смысл. Программа создавалась долго и с перерывами, но отступать мне не хотелось. В начале я просто программировал алгоритмы ПИОНЕРа, проникаясь пониманием модели, не раз переделывая программу, переоткрывая для себя то, к чему пришли в конце 70-х годов математики Ботвинника (Штильман, 1981) — это то, что модель (с точки зрения программирования) является многоуровневой иерархией списков (цепочек) — динамических структур данных (Штильман называет это "динамической иерархией подсистем", 2000). Но когда в 2002 году я нашёл в интернете сайт Бориса Штильмана с его статьями по LG, то очень обрадовался. Значит то, чем я занимался — это не просто программирование игры, а — современная математика. Хотя моя программа ещё может содержать ошибки, да и возможности её пока скромные (ведь в шахматы, как и ПИОНЕР, она не играет), тем не менее, она демонстрирует (для тестовых позиций) процесс построения LG-дерева и показывает (в виде карты полей) на шахматной доске зоны атаки, траектории комля, отрицающих фигур и траектории отступления мишени. |
|
О языке программирования LG-систем |
|
"Зри в корень"
Козьма Прутков
"Мысли и афоризмы", 5. |
|
Непредсказуемая сложность и специфичность программных прототипов LG-систем убеждает, что создавать их нужно на каком-то метаязыке (высокого уровня и ориентированном на LG). В 80-х годах средой для разработки прототипов LG-систем была система PW (Мирный В.Р. и др., 1986; Мирный В.Р., Чудаков М.В., Штильман Б.М., 1988; Stilman B., 1994f, 2000). Метаязык в PW был написан на расширенной версии (алголоподобного) языка Дейкстра (Штильман, 2000):
"Хотя язык Dijkstra (Дейкстра, 1976; Грис, 1983; Штильман, 1994f) был входным языком (транслятора), полностью реализованным в PW, фактическая разработка (включая отладку) проводилась с использованием проблемно-ориентированного языка очень высокого уровня. PW позволила нам создавать, расширять и поддерживать различные версии этого языка и для других проблемных областей. PW была реализована на IBM 370/144 — оригинальном американском компьютере, на котором в эти годы и велась разработка ПИОНЕРа. Позже, PW инструменты использовались в нескольких НИИ на советских ЭВМ для разработки и поддержки крупномасштабных проектов в области Искусственного Интеллекта. Инструменты PW были подготовлены к модернизации для поддержки объектно-ориентированного программирования."
В 90-х годах полноценные прототипы LG-систем успешно создавались на языке CLIPS — функциональном расширении языка LISP (Штильман, 2000):
"Несколько общих LG-грамматик были впервые реализованы в Университете Колорадо в Денвере в 1993 году Д.Кингом и Р.Матьюсом с использованием языка CLIPS и языка C, соответственно (Кинг, 1993) и (Матьюс, 1993). В то время как Р.Матьюс реализовал только два уровня иерархии — Траектории и Зоны (на C), Д.Кинг разработал прототип полномасштабной иерархии грамматик, используя среду программирования CLIPS. Он показал также, что инструменты программирования CLIPS (Гиарратано и Рилей, 1998), предназначенные первоначально для разработки экспертных систем, продемонстрировали высокую эффективность для быстрой реализации LG-грамматик. Конечно, эффективность на этапе разработки была достигнута за счёт снижения эффективности на этапе исполнения. Однако эти инструменты могут послужить основой для разработки прототипов."
Когда я искал язык для написания шахматной программы по Ботвиннику, то был восхищён языком Алгол-68 для ЕС ЭВМ (80-е годы), а затем — языком Модула-2 (начало 90-х годов). Эти языки называют алголо-, паскале-, оберон-подобными языками. Такие языки с жёсткой типизацией дисциплинируют мышление программиста и фактически ведут его за собой (по своей внутренней логике) при разработке сложной программы (с многочисленными произвольными типами данных). Со временем я убедился, что мой стиль программирования очень похож на тот, о котором писал Дейкстра (1976), т.е. я оказался вполне подготовленным для программирования прототипа шахматной LG-системы.
Сейчас моя программа написана на языке Модула-2 с ООП-расширениями для MS DOS.
В перспективе её не сложно переписать на такие языки: P.S. Об этих современных языках можно прочитать на CD-дисках "Мир ПК Диск" 2003-2005 годах — приложениях к журналу "Мир ПК" — в разделе "Студия программирования", который ведёт Руслан Богатырев (bogatyrev@pcworld.ru).
Александр Тимофеев,
г.Харьков, Украина, апрель—июнь 2005 года. http://atimopheyev.narod.ru/AfterPIONEER/index.html |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/index.html |
|
Пишут о проекте ПИОНЕР ( цитаты из статей ) |
О Михаиле Ботвиннике
"Большой Энциклопедический Словарь",
cтатья "Ботвинник"
"Энциклопедия шахмат", раздел
"Ботвинник"
|
МОДЕЛЬ игры
"Энциклопедия шахмат", раздел "Ботвинник"
из главы 5. ЭПИЛОГ
"Энциклопедия шахмат", раздел "Ботвинник"
из главы 1. АЛГОРИТМ МАСТЕРА
"ПИОНЕР",
Как всё начиналось — рассказывает Михаил Моисеевич Ботвинник
"...нашел цель неточной игры в шахматы"
Из гл. "К достижению цели. Алгоритм игры в шахматы" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987e, с.483-484.
"...состоялось обсуждение"
Из гл. "К достижению цели. Алгоритм игры в шахматы" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987e, с.490-491.
"...пришло письмо от Бутенко из Новосибирска с отказом от дальнейшей работы"
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.503-504.
"Б.Штильман работал со всей энергией."
Из Приложения 2 "Как создавался шахматный метод" в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.100.
"...пришлось программу «крестить»"
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.512.
"процесс шахматной игры... состоит в обобщённом размене"
Из кн. Ботвинник, "Алгоритм игры в шахматы", 1968, с.29-30.
"материал и контроль полей"
Из "Послесловия" в кн. Ботвинник, "О кибернетической цели игры", 1975, с.68.
"...если бы Капабланку попросили составить алгоритм игры в шахматы"
Из гл. "Портреты. Х.Р.Капабланка" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987f, с.27.
"Но как эти конъюнктурные стоимости формализовать и вычислять?"
Из ст. "Методом «божьей коровки»" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987, с.246-247.
"размен материальных и конъюнктурных стоимостей фигур..."
Из ст. "Шахматы и принятие решений" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987b, с.241.
"зона игры была превращена в цепочку фигур"
Из кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.15.
"Б.Штильман «покатил налево»"
Из Приложения 2 "Как создавался шахматный метод" в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.103.
"К тому времени мы уже перестали бедствовать с машинным временем."
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.519-520.
"А как же с шахматной программой ?"
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник, "Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.521.
"Лишь когда надо улучшать текущий оптитмальный вариант в переборе"
Из кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.27.
"замена пятнышек на метки потребует новой подпрограммы составления цепочек"
Из кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.27.
"...надо было сделать более экономный и близкий алгоритму мастера вариант программы..."
Из кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.104.
Из статьи кандидата технических наук Валерия Родикова ,
"ЭВМ: Дорога к мастерству", журнал "64 — Шахматное обозрение", СССР, 1980 г., № 4.
Из интервью доктора технических наук, экс-чемпиона мира Михаила Ботвинника
для журнала "Шахматы", СССР, 1987 г., № 11.
Из интервью Михаила Ботвинника
для журнала "Шахматы", СССР, 1975 г., № 7.
Из
выступления Михаила Ботвинника
на семинаре по вопросам шахматной программы ПИОНЕР и современным персональным компьютерам, Москва, СССР, 1988 г.
Из статьи младшего научного сотрудника ВНИИЭ М.Чудакова "Как дела, ПИОНЕР?",
журнал "Шахматы в СССР", 1987 г., № 3.
"Существует легенда, будто Ботвинник стоял у... Но его программа «Пионер» так и не сделала..."
"Осень патриарха. Еврейско-армянская битва во славу русского народа", "Московский комсомолец", Россия, июнь 2003 г.
"...шахматная программа ПИОНЕР прекрасно...",
Шахматный Сатирикон Пьера Собаккина
"...Ботвинник, будучи большим приверженцем ... программой «Пионер»"
OSP.RU:Издательство "Открытые системы", 1999
ICCA members and other interested in Computer Chess
Hans Berliner, Date: 1993-07-09
Botvinnik on Computer Chess
Louis Blair, Date: 6 Oct 89
Botvinnik on Computer Chess
Jonathan Schaeffer, Date: 1996/10/23 "...Didn't Hans Berliner write about this sort of thing in the first page or two of his article about Botvinnik's 'feats'..." Jonathan Schaeffer, Date: 1996/10/23
"...Early Artificial Intelligence (AI) researchers were interested in Chess...",
Сomputers and Chess
|
Рассказывает Михаил Донской
"Михаил Донской: Я Билла Гейтса ни в чем не виню...",
статья Алены Кухаревой, ИД "Компьютерра, 2003. Сайт "Домашний компьютер" — приложение к интернет-изданию "Компьюлента"
"Крупные фигуры",
статья генерального директора компании "DISCO" Михаила Донского, журнал "ИнфоБизнес", Россия, 2002 г.; № 198.
"Каисса",
статья Михаила Донского
"Компьютерные программы, как конец спортивных шахмат",
Ведущий радио "Свобода" Александр Костинский |
МОДЕЛЬ ++ (SmarThink и др.)
SmarThink, на сайте "Рабочей группы по искусственному интеллекту"
Новости компьютерных шахмат,
на сайте "Сергея и Дмитрия"
sdchess.net,
sdchess.net - сайт шахматного программирования |
Шахматный гений: человек или компьютер ?
"Шахматный гений: человек или компьютер ?",
Издательство "Открытые системы" |
О красоте шахмат
"О красоте шахмат"
(размышления писателя и болельщика о стиле Ботвинника и Таля), "Шахматы в России", 1998, №5-6, Владимир Барлас. |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/PIONEER/0.htm |
О Михаиле Ботвиннике
В.Линдер и И.Линдер,
"Большой Энциклопедический Словарь", cтатья "Ботвинник" http://education.kulichki.net/dic/2k.html |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/PIONEER/1.htm |
МОДЕЛЬ игры
"Энциклопедия шахмат", раздел "Ботвинник",
из главы 5. ЭПИЛОГ
"Энциклопедия шахмат", раздел "Ботвинник",
из главы 1. АЛГОРИТМ МАСТЕРА
рассказывает Михаил Моисеевич Ботвинник
http://adamant1.fromru.com/pioneer.html
"...через месяц [1964 г. — Е.М.] написал что-то связное. Впоследствии понял, что написал — нашел
цель неточной игры в шахматы. Потом мне приходилось решать и другие нелёгкие задачи, но эта,
вероятно, оказалась самой трудной. Цель игры — основа алгоритма. На поиск цели в общей
сложности ушло три с половиной года.
Найденная цель игры оказалась весьма простой: надо стремиться к выигрышу материала. Собственно говоря, так интуитивно играет квалифицированный шахматист, но все об этом молчат, ибо обычно этот принцип понимают вульгарно, в том смысле, что в данный момент надо уничтожить наиболее ценную неприятельскую фигуру — это, конечно, ошибочно. Но если эту цель игры понимать так, что надлежит стремиться к оптимальному выигрышу материала в пределах обозримого счёта вариантов, то она представляется вполне разумной. Уже и тогда мне было ясно, что нужно формализовать и понятие позиционной игры, однако пришлось отложить решение этого вопроса. Он был решён много позже."
Из гл. "К достижению цели. Алгоритм игры в шахматы" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987e, с.483-484.
"...состоялось обсуждение [статьи М.Ботвинника о шахматном алгоритме, напечатанной в "Бюллетене Центрального шахматного клуба СССР", Москва, 1966 г. — Е.М.]. Его провели 13 мая 1966 г. в Чигоринском зале клуба; собрались и математики, и гроссмейстеры.
После доклада началась мощная атака: и М.Шура-Бура, и Г.Адельсон-Вельский, и Б.Араманович... Выступил один профессор — вид его был необычайно респектабельный (потом Араманович сообщил, что он окончил Кембридж), — поучал меня, как надо составлять шахматный алгоритм. Неожиданно один молодой человек заявил, что алгоритм Ботвинника ему нравится. — А вы кто такой ? — Бутенко — Откуда ? — Из Новосибирска. Споры разгорелись с новой силой, а после закрытия диспута приняли даже не совсем парламентский оборот. Выпускник Кембриджа слушал-слушал и вдруг неожиданно заявил: "А может, Ботвинник сделал что-то классическое?" Все на него зашикали... На этом диспуте выяснилось одно неожиданное для меня обстоятельство: оказалось, что неизвестны способы получения траекторий на ЭBM. И Шура-Бура, и Адельсон-Вельский утверждали, что простым путём траектории получить невозможно, стало быть, и алгоритм никуда не годится! А с Володей Бутенко мы вскоре начали сотрудничать и работали до 1970 года. Посидел я две недели и нашёл простой метод — с помощью массивов 15х15. Написал статью, отнёс В.Симагину [главному редактору "Бюллетеня Центрального шахматного клуба СССР" — Е.М.], он её тут же опубликовал... Бутенко и сделал программу [в кодах ЭВМ М-20 — А.Т.], которая выдавала необходимые траектории. Мои оппоненты стали осторожнее. Практика показала, что нельзя успешно работать, когда сотрудники живут в разных городах и встречаются друг с другом эпизодически. Наше сотрудничество с В.Бутенко со временем не могло не прекратиться.
Из гл. "К достижению цели. Алгоритм игры в шахматы" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987e, с.490-491. Из книги Михаила Ботвинника "У цели", Россия, 1997 г., с.204-205.
"Только я вернулся в Москву из Лейдена, пришло письмо от Бутенко из Новосибирска с отказом от дальнейшей работы. Субъективно Володя, конечно, ошибся, без меня он уклонился от правильного пути [в 70-х годах программа Бутенко неплохо играла в шахматы — А.Т.]. Объективно Бутенко помог мне своим отказом.
Я считал ранее, что программу должен сделать Бутенко, поэтому держался довольно пассивно, не вникая в различные тонкости работы. Когда я остался один, понял, что требование Криницкого о том, чтобы я разработал блок-схемы алгоритма, справедливо. Пришлось засесть за работу. К тому времени алгоритм продвинулся вперёд. В конце мая 1969 года, во время отдыха в Крыму, я открыл новый элемент алгоритма — зону. Простая зона — это совокупность фигур и траекторий их передвижения, где основной траекторией является траектория нападения атакующей фигуры по направлению к атакованной [т.е. к мишени — А.Т.], другие фигуры либо препятствуют этому нападению (они того же цвета, что атакованная), либо поддерживают (они одного лагеря с атакующей). Оказалось, что такая зона формируется по строго детерминированной структуре, в зону включаются лишь те фигуры, которые успевают принять участие в борьбе. (Бутенко решил, что включение зоны в алгоритм необязательно. Формально мы на этом и разошлись.)
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.503-504.
"Б.Штильман работал со всей энергией. Он сделал подпрограмму поиска траекторий и, после упорного сопротивления, подпрограмму зоны. Б.Штильман не играл в шахматы, [это "шутка" Ботвинника или журналистский приём — А.Т.] он их не понимал: с точки зрения математика зона была не нужна, если она не задана правилами игры.
А.Юдин сделал, в основном, библиотеку эндшпиля."
Из Приложения 2 "Как создавался шахматный метод"
в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.100.
"Кстати, пришлось программу "крестить". В декабре 1976 года пришло из Канады приглашение принять участие во втором чемпионате мира шахматных программ для компьютеров. Требовалось заполнить анкету, где один из вопросов относился к названию программы. Я предложил ЧЕЛОВЕК, ибо программа играет по человеческому методу. Боря предложил ПИОНЕР (оказалось, что это им давно подготовлено), так как программа прокладывает новые пути в области принятия решений. Обсудили и решили, что программе до человека ешё далеко, а пионером она уже является!"
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.512.
"По моему мнению, процесс шахматной игры (и, вероятно, любой игры)
состоит в обобщённом размене. Назовём обобщённым разменом такой размен, где
меняются (в общем случае) ценности как материальные, так и позиционные ("невидимые",
конъюнктурные). Цель обобщённого размена — относительный выигрыш этих
материальных либо позиционных (конъюнктурных) ценностей. Других целей нет и не может
быть. В конечном итоге в шахматах этот обобщённый размен должен привести к выигрышу
бесконечно большой материальной ценности (к мату)."
Ботвинник, "Алгоритм игры в шахматы", "Наука", Москва, 1968,
с.29-30.
"Наконец, о позиционной оценке. С ней связано много сомнений и неудачных
попыток найти разумное решение. Помогла здесь (это можно утверждать, если эксперимент
приведёт к удовлетворительным результатам) моя работа по редактированию "Учебника шахматной
игры" Капабланки. Несколько десятилетий я не заглядывал в эту книгу, теперь, после работы
над алгоритмом, я изучил её с другой точки зрения. Меня поразила
решительность, с которой Капа отверг общие советы по позиционной игре, принятые во всех
руководствах. Капабланка утверждал, что лишь два фактора играют важную роль в шахматах:
материал и контроль полей. Это удивительно близко той цели игры,
которая была провозглашена автором этих строк ещё десять лет назад. Поэтому и нетрудно было
формализовать цель позиционной игры по Капабланке как "контроль полей"!".
Из Послесловия в кн. Ботвинник,
"О кибернетической цели игры", 1975, с.68.
"Грешен, когда я взялся по просьбе издательства за изучение этой книги, то сетовал на свою
слабохарактерность: к чему было соглашаться, ведь работа над шахматной программой быстрей не пойдёт...
Но вскоре настроение переменилось: я убедился, что, если бы Капабланку попросили составить
алгоритм игры в шахматы, он сделал бы примерно такой же алгоритм, что и автор этих строк.
В этом отношении примечательна полемика с Е.Зноско-Боровским: на первое место (в отличии от распространённых представлений)
при оценке позиции Капабланка ставил соотношение по материалу и на второе — контроль полей. Я же
до этих представлений добирался мучительным путём...".
Из гл. "Портреты. Х.Р.Капабланка" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987f, с.27.
"ПИОНЕР плохо анализировал
эту
позицию с точки зрения шахматного мастера.
И тогда я задумался: в чём же дело? Вспомнил то определение шахмат, которое я дал ещё в
1968
году, — шахматная игра представляет собой обобщённый размен материальных и
конъюнктурных стоимостей фигур... Под конъюнктурной стоимостью
подразумевается та реальная сила фигуры, которая проявляется в данный момент сражения
на шахматной доске; материальная же стоимость общеизвестна — это
средняя сила фигуры."
Из ст. "Шахматы и принятие решений", в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987b, с.241.
"Когда в мае 1979 года ПИОНЕРу была дана на анализ позиция из партии
Ботвинник—Капабланка,
он не выдержал экзамена — включал в перебор ходы, по силе
соответствовавшие игре шахматиста второго разряда. К тому времени уже стало ясно, что вершиной
программы выбора хода является приоритет включения ходов в перебор... Если первый включённый
в перебор ход даст хороший результат, то остальные ходы в этой же позиции и изучать
нечего — результат в лучшую сторону не изменится!
Но приоритет был фальшивым, и ПИОНЕР включал в перебор слабые ходы. Этот приоритет основывался на средних (материальных) стоимостях фигур... Ещё в 1968 году в книжке "Алгоритм игры в шахматы" я писал, что “по моему мнению, процесс шахматной игры (и, вероятно, любой игры) состоит в обобщённом размене. Назовём обобщённым разменом такой размен, где меняются (в общем случае) ценности как материальные, так и позиционные ("невидимые", конъюнктурные)”. В отличии от материальной стоимости, соответствующей средней силе фигуры, конъюнктурная соответствует реальной силе фигуры в данный момент сражения на шахматной доске. Но как эти конъюнктурные стоимости формализовать и вычислять ? Когда в 1978 году составлялась подпрограмма размена материальных стоимостей фигур на каком-либо поле доски, учитывалось, что одна и таже фигура может участвовать в разменах на разных полях. На всякий случай было решено присваивать фигуре "пятнышко" (метку) от каждого размена (метод этот был назван методом "божьей коровки", поскольку у неё тоже есть пятнышки)... Ранее траектории движения фигуры присваивался материальный приоритет, основанный на размене материальных стоимостей (этот приоритет и давал ошибочный результат). Теперь было принято, что значение этого приоритета определяет величину пятнышка той фигуры, которая с этой траекторией связана (по размену на поле). У фигуры уже появились "пятнышки" разной величины. По этим пятнышкам и определялась конъюнктурная стоимость фигуры. На смену приоритету материальному пришёл приоритет конъюнктурный. ПИОНЕР и стал искать ход, как мастер."
Из ст. "Методом "божьей коровки"", в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1980a, с.246-247.
"В 1981 г. оторванная от реальной доски зона игры была превращена
в цепочку фигур. Главное отличие состояло в том, что траектории движения фигур
определялись уже на заставленной фигурами доске."
кн. Ботвинник,
"Шахматный метод решения переборных задач", 1989, с.15.
"Б.Штильман по шахматной программе действовал один. А когда в декабре 1982 года я вернулся к шахматной программе, картина представлялась тревожная: Б.Штильман "покатил налево". В переборе он исследовал позицию не на всей доске, а в наиболее "важной" цепочке... Разве так играет мастер?
Пришлось мне предложить исправленный алгоритм. Штильман, который слабо понимал шахматную игру, не осознал своей ошибки. А ведь пропала часть работы и предстояла новая... Он и рассердился, и обиделся. Но что было делать? Коллеги мне друзья, но шахматы дороже!" [Это писалось в 1989 году после того, как уволились Мирный и Штильман. Однако ещё в 1981 Штильман подавал заявление об уходе, из-за разногласий с Ботвинником — А.Т.]
Из Приложения 2 "Как создавался шахматный метод"
в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.103.
"Приставал ко мне Саша Резницкий.
— Давайте опубликуем статью о ПИОНЕРе 2.4. Мне же это для защиты нужно... Речь шла о кандидатской работе. — Разве вы не знаете, что нормальным путём она может быть опубликована лишь через несколько лет? Впрочем... Вспомнил я о злосчастном совещании 1979 года. А что, если обратиться за помощью к тому, кто тогда председательствовал? Он же должен понять, что работа серьёзная — раз привела к таким результатам? Не ошибся — нас поддержали, и через несколько месяцев статья была опубликована в журнале "Экономика и математическое методы". К тому времени мы уже перестали бедствовать с машинным временем. Академик В.М.Глушков в начале 1982 года руководил совещанием по шахматным программам. С возмущением он узнал, что у нас нет выхода на ЭВМ. Пошёл Виктор Михайлович в ГКНТ и договорился о компьютере; но нужны были деньги на оплату машинного времени (и немалые). Написал я письмо председателю ГКНТ Г.И.Марчуку. Познакомились мы с Гурием Ивановичем ещё в 1968 году в Новосибирске; директор ВЦ был председателем ГЭК факультета — я приезжал на дипломную защиту Бутенко. Распоряжение о выделении необходимых средств было дано. Но как их получить? Следовало оформить постановление ГКНТ о нашей работе."Вопрос мелкий, специального постановления не будет, ждите общего решения. Впрочем, можете обратиться к нашему начальнику Е.И.Валуеву". Звоню. — Евгений Иванович, с вами говорит Ботвинник, я когда-то играл в шахматы... — Михаил Моисеевич, что это вы со мной так странно разговариваете?... Вот это да! Оказывается, зампред Спорткомитета, который открывал один из моих матчей, и начальник управления финансирования ГКНТ — одно и то же лицо! Постановление было принято, и работа возобновилась. Вопрос с защитой моих сотрудников оказался сложным: математические Советы (куда мы обращались) отказывались поддержать работу Штильмана — метод "Пионер", мол, сомнителен, научно не обоснован. Я понимал, что защита возможна лишь в Совете ВНИИЭ, поскольку этот "сомнительный" метод блестяще проявил себя на энергетической задаче. Но и в нашем институте противодействие было сильным — считались с мнением математических светил. Но нашлись союзники и среди математиков. Ещё в 1979 году акдемик В.М.Глушков, Н.И.Красовский и профессор В.А.Якубович дали согласие войти в Совет ВНИИЭ, что необходимо при защите "на стыке" двух специальностей (эенергетики и математики). В 1983 году Виктора Михайловича уже не было в живых, Николай Николаевич и Владимир Андреевич подтвердили своё участие в защите. Наконец в институте всё согласовано, и осталось получить лишь разрешение ВАК на защиту Штильмана. И здесь — полный "стоп". Сначала запрет (в нарушении собственных инструкций ВАК), затем при повторном запросе — молчание. Что делать? Снова пишу тому, кто председательствовал на злополучном совещании. Через неделю разрешение ВАК получено... В декабре 1984 года защиты состоялись. Сначала выступал Резницкий, чтобы члены совета прежде всего ознакомились с результатами применения метода, а затем Штильман изложил суть метода. Всё благополучно завершилось. Гора с плеч." 
Борис Штильман.
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.519-520.
"А как же с шахматной программой ?
С ней дела слабее. Создаётся впечатление, может быть ошибочное, что математики не торопятся... Ступень системы — зона была заменена на цепочку... "Проходимость" цепочки ([которая] подсчитывается по материальным разменам на полях траектории) равна проходимости траектории нападения,... [при условии, что] игра в цепочке пришла бы к своему логическому завершению. Величина этой проходимости и является "пятнышком" цепочки. Совокупность цепочек образует математическое отображение позиции. В процессе поиска хода оно изменяется. В этом состоит принципиальное отличие "шахматного" метода решения переборных задач от традиционных. Математики создают модель задачи, а затем приступают к решению. Шахматист при поиске решения следит за изменением отображения задачи — оно помогает найти решение и при этом меняется в процессе самого решения. Позиционное понимание шахматиста связано с тремя факторами: 1) соотношением материала, 2) усиливающейся надеждой на выигрыш материала и 3) собственно позиционной составляющей, базирующейся на владении полями доски и на "пятнышках" цепочек. На этом же базируется и приоритет хода, который включается в перебор. Тот ход, что приводит к наиболее благоприятному изменению отображения, и является приоритетным."
Из гл. "К достижению цели. Искусственный шахматист" в кн. Ботвинник,
"Аналитические и критические работы 1928-1986. Статьи. Воспоминания", 1987ee, с.521-522.
"В программе сейчас каждая фигура имеет так называемое
"пятнышко", отображающее проходимость пучка траекторий с этой фигурой
и без фигуры... Экономнее давать фигуре — участнице игры в цепочке лишь
"метку", не высчитывая числа, отображающего роль фигуры в цепочке.
Лишь когда надо улучшать текущий оптитмальный вариант в переборе (см.
этюд Надареишвили
) необходимо численно определять роль этой фигуры в игре (для вычисления
приоритета)".
Ботвинник,
"Шахматный метод решения переборных задач", 1989, с.27.
"Подпрограммы понимания и приоритета в шахматной программе в основном разработали Б.Штильман и В.Мирный. Они утверждали, что эти части программы в порядке, хотя приоритет иногда и фальшивил."
Из Приложения 2 "Как создавался шахматный метод"
в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.103.
"И, наконец, конъюнктурный размен. Сейчас в
программе есть и однократный и многократный конъюнктурный размен. Последний — когда на поле,
куда ступает фигура, возможны взятия. Это и нелогично, поскольку на других полях также
возможны взятия; но эти взятия не проверяются. Многократный размен требует большого расхода
ресурсов, да и подпрограмма многократного размена весьма сложна. Введен он был, поскольку не
видели иной возможности определения Mg*. Однако теперь формализовано определение
Mg* и в однократном конъюнктурном размене с помощью траекторий
оттеснения и отвлечения (в надежде, что фигура будет оттеснена или
отвлечена). Это также предполагается включить в новый вариант
программы. Добавим, что замена пятнышек на метки потребует новой
подпрограммы составления цепочек".
Ботвинник,
"Шахматный метод решения переборных задач", 1989, с.27.
"В конце 1986 г. общий алгоритм подпрограммы составления и анализа дерева перебора был готов. М.Чудаков быстро составил программу перебора, и тогда тайное стало явным: в программе, и именно в понимании и приоритете, оказалось множество ошибок.
Да и выловить их было делом сложным. Программисты (не шахматисты) сделали программу столь сложной, неоптимальной и громоздкой, она работала столь медленно, что за год (!) реального продвижения в отладке задачи не было. [Видимо, речь идёт о PW. Но это писалось в 1989 году после того, как уволились Мирный и Штильман. Сквозь эти строки "сочится" обида Ботвинника на уход Штильмана. Мой же 10-ти летний опыт программирования алгоритмов ПИОНЕРа показывает, что это нормальная ситуация — А.Т.]. Математики были самоуверены, не признавали моего шахматного авторитета. Любое шахматное дополнение в алгоритме годами встречало упорное сопротивление. Так, пресловутое Mg* — жертвенная комбинация, введенная Греко в практику шахмат почти 4 века назад, — впервые представлено было для использования в 1982 г. Ранее была установлена чёткая процедура изменения алгоритма (и не только в шахматной программе): любое изменение обязательно должно быть представлено для обсуждения в письменном виде. После дискуссии руководитель принимает решение, обязательное к исполнению. Таких изменений и дополнений накопилось с 1974 г. около четырёхсот! Увы, обязательности исполнения решений нередко и не было... Повторяем, письменное предложение относительно Mg* было сделано впервые в 1982 г. — и принято. А осенью 1987 г. математики втихаря исключили Mg* из формулы оценки позиции при обрыве варианта в дереве перебора. Конфликт нарастал. Со многим я мирился: с различными несоответствиями алгоритму мастера, с недисциплинированностью сотрудников. Но когда положение изменилось, надо было сделать более экономный и близкий алгоритму мастера вариант программы — занял жёсткую позицию...
Из Приложения 2 "Как создавался шахматный метод"
в кн. Ботвинник, "Шахматный метод решения переборных задач", 1989, с.104. |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/PIONEER/2.htm |
Рассказывает Михаил Донской
"Михаил Донской: Я Билла Гейтса ни в чем не виню...",
Статья Алены Кухаревой, ИД "Компьютерра, 2003. Сайт "Домашний компьютер" — приложение к интернет-изданию "Компьюлента". http://dk.compulenta.ru/offline/2002/73/18985/
"Крупные фигуры",
статья генерального директора компании "DISCO" Михаила Донского, журнал "ИнфоБизнес", Россия, 2002 г.; № 198. http://www.ibusiness.ru/offline/2002/198/16515/
Оригинал статьи представлен на сайте
www.computer-museum.ru
Рассказывают Михаил Донской и Александр Битман
Передача прозвучала в эфире Радио Свобода 26.02.02
Ведущий радио "Свобода" Александр Костинский http://www.svoboda.org/programs/sc/2002/sc.022602.asp |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/PIONEER/3.htm |
МОДЕЛЬ ++ (SmarThink и др.)
Сайт "Рабочей группы по искусственному интеллекту"
http://www.aigroup.narod.ru/news.htm |
Сайт "Рабочей группы по искусственному интеллекту"
http://aigroup.narod.ru/details1r.htm |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/PIONEER/4.htm |
www.osp.ru::Издательство "Открытые системы"::
Информационные технологии::Computerworld::Технологии:: "Шахматный гений: человек или компьютер ?" http://www.osp.ru/cw/2005/10/038_1.htm |
|
http://atimopheyev.narod.ru/AfterPIONEER/info/PIONEER/5.htm |
"О красоте шахмат
(размышления писателя и болельщика о стиле Ботвинника и Таля)", "Шахматы в России", 1998, №5-6, Владимир Барлас http://www.berkovich-zametki.com/Nomer22/Barlas2.htm |
|
http://atimopheyev.narod.ru/EncyclopediaChess/Info/index.html |
|
|
http://atimopheyev.narod.ru/Mansurov/index.html |
|
|
http://atimopheyev.narod.ru/LG01pdf_in_HTML/index.html Linguistic Geometry From Search to Construction Boris Stilman University of Colorado at Denver & STILMAN Advanced Strategies, LLC Kluwer Academic Publishers Boston Dordrecht London |
|
|
|
Лингвистическая Геометрия
От Перебора к Построению Борис Штильман Университет Колорадо в Денвере & STILMAN Advanced Strategies, LLC Kluwer Academic Publishers Бостон, Дордрехт, Лондон |
|
|

Для заказа этой книги свяжитесь с
Kluwer Academic Publishers по адресу http://www.wkap.nl/series.htm/ORCS Оригинал LG01.pdf на английском языке доступен в Интернете на web-сайте Бориса Штильмана по адресу: http://www.stilman-strategies.com/bstilman/research/BOOKpdfs/LG01.pdf |
|
|
|
Штильман Борис,
Лингвистическая Геометрия: от Перебора к Построению, 1999, 395 стр. LG — математическая дисциплина, которая занимается поиском лучших стратегий в переборных задачах, относящихся к классу игр на абстрактной доске. LG выросла из проекта шахматной программы ПИОНЕР М.Ботвинника, в котором Борис Штильман был ключевым математиком и программистом. Удивительно то, что сейчас приложения LG — это управление навигацией роботов и беспилотных транспортных средств, моделирование боевых операций, составление расписаний, а не только шахматы или другие настольные игры. В отличие от традиционных подходов к поиску стратегий на дереве перебора, LG позволяет за разумное время вычислять лучшие и даже теоретически оптимальные стратегии в реальных боевых задачах. Copyright © 1999 Борис Штильман. Все права охраняются законом. Никакая часть этой публикации не может быть воспроизведена, сохранена в базе данных, дистрибьютирована или передана в любой форме или любыми другими средствами — электронными, механическими, фотокопированием, записью или иначе — без предшествующего письменного разрешения Бориса Штильмана. |
|
|
|
|
|
ОГЛАВЛЕНИЕ
Титульная страница книги ПРЕДИСЛОВИЕ к переводу LG01.pdf на русский язык ПРЕДИСЛОВИЕ БЛАГОДАРНОСТИ 1. Введение......................................................................1 1.1 Проблематика.................................................................2 1.2 Современные подходы..........................................................4 1.3 LG с первого взгляда.........................................................9 1.4 Углублённое рассмотрение LG-подхода.........................................13 1.5 Стратегии LG и Теория Игр...................................................19 1.6 Три этапа развития LG.......................................................22 1.7 Этап 1: Проект ПИОНЕР.......................................................24 1.8 Этап 2: Математические Инструменты..........................................28 1.9 Этап 3: Новейшая История....................................................32 2. Иерархии Формальных Языков...................................................39 2.1 Обзор Иерархии..............................................................39 2.2 Классы Задач................................................................40 2.3 Различные Задачи как Сложные Системы........................................45 2.4 Множество Путей: Язык Траекторий............................................50 2.5 Расстояния на Доске и в Пространстве Состояний..............................52 2.6 Сети Путей: Языки Сетей.....................................................54 2.7 Представление Движения: Переводы............................................66 2.8 Перебор через Построение: Языки Переборов...................................71 2.9 Исторические Замечания......................................................75 3. Бой Роботов в двумерной Области..............................................77 3.1 Постановка Задачи...........................................................77 3.2 LG-перебор..................................................................79 3.3 Обсуждение..................................................................88 3.4 Исторические Замечания......................................................89 4. Переход в трёхмерное Пространство............................................91 4.1 3D/4A - Бой Роботов.........................................................91 4.2 LG-перебор в пределах недостаточного Горизонта..............................94 4.3 LG-перебор в пределах Горизонта 5...........................................98 4.4 Переход от 2D к 3D: Изменение Времени Выполнения...........................105 4.5 Исторические Замечания.....................................................106 5. Более глубокий Перебор, больше Агентов......................................107 5.1 2D/8A - Воздушный бой......................................................107 5.2 Глубокий Перебор для Воздушного Боя........................................112 5.3 3D/8A - Космический Бой....................................................128 5.4 Новый Уровень Сложности: Предварительные Выводы............................131 5.5 Исторические Замечания.....................................................134 6. Параллелизм, n×n Область....................................................137 6.1 Ослабление Последовательного Режима: Частичный Параллелизм.................137 6.2 LG-перебор для Задачи с Частичным Параллелизмом............................139 6.3 Вторая Задача с Частичным Параллелизмом....................................143 6.4 Вторая Задача: LG-перебор..................................................145 6.5 Задача с Полным Параллелизмом и n×n Областью...............................150 6.6 Задача с Полным Параллелизмом: LG-перебор..................................155 6.7 Воздействие Параллелизма...................................................160 6.8 Исторические Замечания.....................................................162 7. Составление Расписаний: Искусственный Конфликт..............................165 7.1 Постановка Задачи..........................................................165 7.2 Преобразование в Игру двух игроков.........................................168 7.3 Составление Расписаний: Перебор и Решение..................................172 7.4 Формальное Представление...................................................174 7.5 Оценка и Реализация........................................................177 7.6 Применимость LG............................................................178 8. Методы Генерации............................................................181 8.1 Грамматики Хомского........................................................181 8.2 Управляемые Грамматики: Введение...........................................183 8.3 Ханойская Башня: 3 Диска...................................................184 8.4 Ханойская Башня: n Дисков..................................................186 8.5 Управляемые Грамматики: Формальное Определение.............................188 8.6 Исторические Замечания.....................................................191 9. Язык Траекторий.............................................................193 9.1 Кратчайшие Траектории: Порождающая Грамматика..............................193 9.2 Генерация Кратчайших двумерных Траекторий..................................196 9.3 Генерация Кратчайших трехмерных Траекторий.................................200 9.4 Кратчайшие Траектории: Корректность и Полнота..............................204 9.5 Допустимые Траектории: Порождающая Грамматика..............................207 9.6 Обход Препятствий: Генерация Допустимых Траекторий.........................210 9.7 Допустимые Траектории: Корректность и Полнота..............................215 9.8 Траектории для Игры в Шахматы..............................................219 9.9 Траектории для Составления Расписаний......................................224 9.10 Траектории для Агентов с Переменной Скоростью.............................226 9.11 Язык Траекторий: Эффективная Реализация...................................232 9.12 Исторические Замечания....................................................233 10. Язык Зон...................................................................235 10.1 Грамматика Зон............................................................235 10.2 Генерация Зон.............................................................238 10.3 Геометрия Зон.............................................................250 10.4 Зоны для Игры в Шахматы...................................................253 10.5 Зоны для Составления Расписаний...........................................254 10.6 Исторические Замечания....................................................256 11. Переводы...................................................................259 11.1 На пути к Решению Проблемы Отличий........................................259 11.2 Теорема о Переводах.......................................................265 11.3 Перебор с Переводами......................................................278 11.4 Переводы и Застывание.....................................................284 11.5 Исторические Замечания....................................................286 12. Языки Перебора.............................................................287 12.1 Общий Перебор.............................................................287 12.2 Сокращённый Перебор.......................................................290 12.3 Грамматика Переводов......................................................294 12.4 Качество Траекторий и Зон.................................................297 12.5 Процедура Обхода Дерева...................................................300 12.6 Исторические Замечания....................................................303 13. От Перебора к Построению...................................................305 13.1 Постановка Задачи.........................................................305 13.2 Обзор Алгоритма...........................................................306 13.3 Предварительные Определения...............................................307 13.4 Расширение Терминальных Множеств..........................................308 13.5 Структура Расширенных Терминальных Множеств...............................311 13.6 Диаграмма Пространства Состояний..........................................319 13.7 Обзор Потенциальных Стратегий.............................................323 13.8 Построение Стратегий из Начального Состояния..............................330 13.9 Стратегии для Рети-подобных задач.........................................335 13.10 Обсуждение...............................................................337 13.11 Исторические Замечания...................................................339 14. Вычислительная Сложность...................................................341 14.1 Время Выполнения: Традиционные Алгоритмы для Рети-подобных задач..........341 14.2 Время Выполнения: Грамматика Кратчайших Траекторий........................347 14.3 Время Выполнения: Грамматика Зон..........................................350 14.4 Время Выполнения: Разворачивание Пучков Траекторий и клонирование Зон.....353 14.5 Вычислительная Сложность: Рети-подобные задачи............................357 14.6 Исторические Замечания....................................................359 Взгляд в будущее...............................................................361 Литература.....................................................................363 Индекс.........................................................................377 Этюды |
|
|
| ПРЕДИСЛОВИЕ |
|
Эта книга не о лингвистике и не о геометрии. Она — о переборных задачах. Лингвистическая Геометрия (LG) — это подход к построению математических моделей для представления знаний и логического вывода в крупномасштабных многоагентных системах. Множество таких систем (формально определяемых здесь как Сложные Системы), включая воздушный бой, роботизированное производство, конверсию программного обеспечения, кибервойну в Интернете и т.д., образуют все те системы, которые могут быть смоделированы как абстрактные настольные игры (ABG). Сложные Системы — это игры многих игроков, ходы которых могут быть представлены передвижениями абстрактных фигур по полям абстрактной доски. Размерность (пространства) абстрактной доски (2D, nD и даже его нелинейность), его форма и размер, подвижность фигур, очерёдность ходов (включая одновременные ходы) — всё это может быть использовано для моделирования разнообразных многоагентных систем. Таким образом, абстрактные настольные игры понимаются здесь как класс Сложных Систем. Цель LG состоит в том, чтобы обеспечить участников игры стратегиями, необходимыми для достижения их целей. Традиционно, чтобы найти такие стратегии нужно перебрать все ветви в гигантском дереве игры (ДИ). Такой перебор часто превышает (по ресурсам времени и памяти) возможности современных и даже мыслимых компьютеров будущего. LG позволяет значительно уменьшить объём перебора, делая переборные задачи решаемыми. LG обеспечивает формализацию и обобщение эвристик перебора, заимствованных у лучших экспертов. По существу, эти эвристики заменяют перебор построением стратегий. Формализованные экспертные стратегии вполне масштабируемы, т.е. они приводят к эффективным алгоритмам для приложений, размерности которых могут быть значительно больше тех, для которых эксперты разрабатывали свои стратегии. Кроме того, эти формальные стратегии позволили в различных областях решать новые задачи, с которыми эксперты ещё не сталкивались. Удивительно то, что для некоторых классов задач эти экспертные стратегии доказуемо приводят к оптимальным решениям. Чтобы формализовать эвристики, LG использует теорию формальных языков (т.е. формальную лингвистику), а также некоторые геометрические структуры на абстрактной доске. Поскольку обе дисциплины — лингвистика и геометрия — были использованы совместно, этот подход был назван Лингвистической Геометрией. Это первая книга по предмету. Я не намеревался представить здесь полную теорию LG, поскольку она ещё не закончена. Однако, эта книга включает основы теории LG. LG имеет длинную и поучительную историю. Шахматы — дрозофила искусственного интеллекта (ИИ) — наибольшим образом способствовали созданию LG. Они и теперь остаются постоянным источником идей и движущей силой, подталкивающей развитие LG. Начавшись с компьютерных экспериментов в 1972 году, продолженных уже с развитием теоретических идей в 80-х и формально определившаяся в 1991, LG развивалась по многим направлениям. Некоторые из них основаны на строгих теоретических построениях, другие — на сложных и утонченных экспериментах. Цель этой книги состоит в том, чтобы представить читателю разнообразие подходов, идей и экспериментов. Каждая глава написана как эссе на одну тему в LG, теоретическую или экспериментальную, хотя все главы связаны вместе и поддерживают друг друга. Глава 1 включает введение в предмет и краткую историю исследований. Глава 2 включает основные определения и обзор формализмов LG, т.е. иерархию формальных языков. Главы 3-7 охватывают несколько экспериментов с инструментами LG. Они демонстрируют, как алгоритмы LG решают задачи постепенно возрастающей сложности. Помимо интересных фактических результатов, детальное описание экспериментов предназначено развить интуитивное понимание алгоритмов LG и их общей структуры. Вооруженный этой интуицией, читатель будет способен воспринять формальное описание инструментов LG, приведенное в главах 8-12. В главе 13 основы LG рассмотрены более глубоко. Пересматривая эксперименты из главы 3, мы вводим новое направление в LG: решение переборных задач путём построения стратегий (без какого-либо перебора на дереве). В главе 14 мы обсуждаем некоторые вопросы вычислительной сложности. В этой книге высказывается предположение, что инструменты LG позволяют выделить широкий подкласс легко решаемых задач (т.е. полиномиально сложных) среди тех, которые обычно считались трудноразрешимыми (т.е. экспоненциально сложными). Алгоритмы LG обеспечивают эффективное решение задач из этого подкласса. Книга может использоваться как учебник для дипломированного специалиста или старшекурсника по курсу LG в течение одного-двух семестров или в качестве приложения к курсу по ИИ. Часть этого материала преподавалась в курсе Представление Знаний для Интеллектуальных Систем и в курсе Сложных Интеллектуальных Систем в Университете Колорадо в Денвере. Также, многие из тем, включенных в эту книгу, ранее преподавались в качестве отдельных лекций и кратких курсов по LG, проводимых по всему миру. Я надеюсь, что читатель разделит мою увлечённость предметом и присоединится к армии исследователей и практиков, которые развивают теорию и приложения LG. Книга не может полностью отразить постоянное развитие LG, она вовсе не предназначена для того, чтобы стать неоспоримым "священным" источником информации по LG в течение многих десятилетий. Моё намерение состоит в том, чтобы раздвинуть границы наших знаний, вызвать интерес, послужить толчком к дальнейшим исследованиям и, тем самым, побыстрее состарить эту книгу и написать новую, которая позволит ещё больше революционизировать наше понимание предмета. Борис Штильман, Денвер, Колорадо, США,
E-mail: bstilman@cse.cudenver.edu
Web: http://www.cudenver.edu/~bstilman/index.html Web: http://www.stilman-strategies.com/bstilman/index.htm Web: http://www.stilman-strategies.com/index.htm |
|
|
| БЛАГОДАРНОСТИ |
|
Я не смог бы написать эту книгу о Лингвистической Геометрии, если бы этому не предшествовало почти три десятилетия исследований. Это работа никогда бы не достигла нынешних высот без поддержки моего научного руководителя, моих коллег и ученых со всего мира, агентств, финансирующих научные исследования, и вычислительных центров. Эта книга была вдохновлена результатами долгого и плодотворного сотрудничества в 70-х и 80-х годах с профессором Михаилом Ботвинником, моим научным руководителем и лидером проекта ПИОНЕР. В самом начале работы он формировал мои взгляды на сложные переборные задачи. Один ученый как-то сказал, что эта невообразимо трудная работа, возможно, началась только потому, что Ботвинник-шахматист не представлял себе трудностей программирования, в то время как Штильман-математик и программист не представлял себе трудностей игры в шахматы. Каждый раз, когда у группы исследователей возникали серьёзные проблемы в работе над проектом ПИОНЕР, доктор Ботвинник имел обыкновение говорить: “Если человек, шахматный мастер, может это делать, то и компьютер тоже сможет это сделать”. Он верил в существование общего алгоритма или небольшого набора общих алгоритмов, интуитивно используемых всеми шахматными мастерами и гроссмейстерами при игре в шахматы. В сущности, разработка, моделирование и обобщение этих алгоритмов и было целью проекта ПИОНЕР. Попытка разработки и исследования математической модели, основанной на этих алгоритмах — цель этой книги. Александр Юдин, Александр Резницкий, Михаил Цфасман, Михаил Чудаков работали со мной в 70-х и 80-х годах над проектом ПИОНЕР. Мой друг и коллега, Вадим Мирный, с которым мы работали в 80-х, проявил глубокую научную проницательность и продвинул наши исследования и программные реализации на значительно более высокий уровень. Также, в 70-х годах неоценимая помощь в разработке программного обеспечения была оказана Дмитрием Лозинским, Лидией Полтавец и Анатолием Кострюковым. Четверо знаменитых ученых, основателей информатики и разработки компьютеров в прежнем Советском Союзе, академик Виктор Глушков, профессора Башир Рамеев, Вячеслав Мясников и Николай Криницкий помогали организации работы, обеспечению финансирования и доступа к современным компьютерам в рамках проекта ПИОНЕР. Проект ПИОНЕР и первые теоретические обобщения, связанные с созданием LG, не увенчались бы успехом без постоянной поддержки многочисленных советских ученых. Я благодарен им всем. Я хотел бы выразить признательность тем, чья решительная поддержка приходила в самые трудные времена. Это академик Николай Красовский, член-корреспондент, лауреат Ленинской премии Яков Цыпкин, члены-корреспонденты Юрий Руденко и Гермоген Поспелов, профессора Дмитрий Поспелов, Давид Юдин, Владимир Якубович, Георгий Адельсон-Вельский, Юрий Шакарян, Гавриил Шалыт, Лев Мамиконянц и доктор Михаил Донской. Научный обмен с исследователями всего мира позволил нашей группе преодолевать изоляцию прежнего Советского Союза. Список основных участников этого сотрудничества включает профессора Монти Ньюборна (Monty Newborn) из Мак-Гилльского Университета, Канада; профессоров Тони Марсланда (Tony Marsland) и Рэнди Гобеля (Randy Goebel) из Университета Альберты, Канада; профессора Япа ван ден Херика (Jaap van den Herik) из Университета Лимбурга, Нидерланды; профессора Бена Миттмана (Ben Mittman) из Северо-западного Университета, США; доктора Дэвида Каландера (David Cahlander) из CDC Corp., США; Кена Томпсона (Ken Thompson) из Лабораторий Белла (Bell Labs), США; доктора Ханса Мойера (Hans Meuer) из Университета Мангейма, Германия; доктора Х.Дж.Аппелрата (H.J.Appelrath) из Университета Дортмунда, Германия; Дэвида Леви (David Levy) из Лондона, Великобритания. Я особо признателен профессору Ньюборну, который пригласил меня для проведения исследований в Мак-Гилльском Университете в 1990 году. Уверен, что без этого приглашения я не смог бы продолжить исследования по LG. В 1992 году профессор Эрвин Родин (Ervin Rodin) из Вашингтонского Университета в Сент-Луисе, Миссури, проявил интерес к дальнейшему развитию и расширению исследований по LG. В качестве главного редактора международного журнала "Компьютеры и Математика с Приложениями" (Computers and Mathematics with Applications), он писал: “... Я был бы очень заинтересован в публикации Ваших работ на эту тему (по LG — Б.Ш.)” (Родин, 1992). Некоторые из основных результатов, представленных в этой книге были впервые опубликованы в этом журнале. Центр профессора Родина "Оптимизация и Семантическое Управление" в Вашингтонском Университете внес вклад в успех 1-го Симпозиума по LG и Семантическому Управлению в 1995 году. В 1994, в связи с применением LG к моделированию и управлению боем, он писал: “Я знаком с работами профессора Штильмана по Лингвистической Геометрии и полагаю, что LG — это может быть наиболее заслуживающий внимания инструмент для выше названного предмета (интеллектуальное планирование и управление боем — Б.Ш.)” (Родин, 1994). В 1993 году доктор Раймонд Луззана (Raymond Lauzzana), главный редактор международного журнала "Языки Проектирования" (Languages of Design) заинтересовался расширением круга специалистов знакомых с возможностями LG. Он приложил значительные личные усилия, осуществлял руководство и поддержку при переработке мною статей по LG для публикации в его журнале, чтобы сделать LG доступной для самого широкого круга специалистов. Он писал: “... Я хотел бы сказать, что доктор Штильман продемонстрировал увлекательный, впечатляющий новизной подход к научным исследованиям. Ему удалось превратить свои исследования по моделированию игр двух игроков в разработку общей модели иерархических систем. Это значительно расширило применимость его работ по LG... Я лично высоко оцениваю строгость, с которой он подошёл к предмету. Я уверен, что его работа окажет существенное влияние в будущем” (Луззана, 1993). Джим Раш (Jim Rash), ученый из Центра Космических Полётов им. Годдарда (NASA), Гринбелт, MD, оказал поддержку, стимулировал и поощрял дальнейшее развитие LG. В качестве приглашённого редактора специального выпуска международного журнала "Телематика и Информатика" (Telematics and Informatics), включающего лучшие статьи Конференции по Космическим Приложениям ИИ 1994 года, он упомянул мою статью "Эвристические Сети для Исследования Космоса" (1994c), “... как пример особенно увлекательного приложения ИИ... Эта статья представляет Лингвистическую Геометрию как эффективный метод для поиска решений в больших пространствах состояний для классов задач, которые известны как особенно трудные, и применяет LG к задаче автономного планирования навигацией робота” (Раш, 1994). Я благодарен профессору Алексу Майстелу (Alex Meystel) из Дрексельского (Drexel) Университета, за его конструктивный интерес к LG и постоянную поддержку. Как главный редактор серии книг по Интеллектуальным Системам, публикуемых издательством Вайли (Wile Series in Intelligent Systems), он не только поощрял меня к быстрому завершению работы над этой книгой, когда я находился ещё в самом начале работы над ней, но даже убеждал написать новую книгу по LG, возможно, с другим акцентом. Профессор Майстел писал: “... Я ожидаю, что многочисленные новые результаты по LG будут включены в Инженерию Знаний ИИ. Любое дальнейшее продвижение в области ИИ невозможно себе представить без использования концептуальных систем подобных Лингвистической Геометрии” (Майстел, 1998). Схему этой книги мне неявно подсказал профессор Норман Фу (Norman Foo) из Университета Нового Южного Уэльса, Сидней, Австралия, который писал: “Не может быть никакой панацеи для методов перебора, поскольку доказано, что в худшем случае перебор экспоненциально сложен или даже ещё сложнее. Так, для любой идеи перебора найдутся такие классы задач, в которых она потерпит поражение. Однако вполне возможно, что существуют большие подклассы задач, которые могут быть хорошо описаны и окажутся поддающимися эффективной атаке. Это как раз то место, где идеи Бориса в области Лингвистической Геометрии представляют интерес. Он по существу нашел интересный и полезный подкласс, для которого его идеи и представления обещают эффективные решения. Это — значительный вклад в область ИИ” (Фу, 1996). Когда работа над этой книгой была почти закончена, я узнал о следующем заявлении профессора Джона Маккарти (John McCarthy) из Стэнфордского Университета. В своих комментариях о решении шахматного этюда Рети компьютерами он писал: “Обратите внимание, что идея Рети может быть реализована на доске размером 100x100, и люди всё ещё смогут решать эту задачу, но современные программы (традиционные, т.е. работающие по методу "брут форс" — Б.Ш.) уже не смогут... Шахматы по-прежнему будут служить дрозофилой для ИИ, если исследователи попробуют создать программу, которая сможет решать задачи на доске произвольного размера. Однако, ИИ не будет продвигаться к человеческому уровню, если исследователи ИИ удовлетворятся методом "брут форс" как заменой интеллекта... Будет ли кто-нибудь серьёзно утверждать, что компьютер не сможет решить этюд Рети методом, отличным от "брут форс"?” (Маккарти,1998). Конечно, LG была разработана независимо и за длительный период времени. Однако, удивительно, что исследования по LG вдохновлялись аналогичными идеями. LG значительно обогатилась при использовании уникальной экспертизы двух учёных, моих друзей доктора Владимира Яхниса (Vlad Yakhnis) из Научного Центра фирмы Рокуэлл (Rockwell Science Center), CA и доктора Александра Яхниса (Alex Yakhnis) из фирмы Пионерские Технологии (Pioneer Technologies), TX. Они внесли существенный вклад в построение выигрышных стратегий для игр двух игроков с полной информацией. Их работа повлияла на определение абстрактных настольных игр, используемых в LG. Я пользуюсь случаем, чтобы выразить особую благодарность доктору Владимиру Яхнису, который способствовал перестройке оснований LG. Я высоко оцениваю рецензию предварительного варианта этой книги, подготовленную доктором Александром Яхнисом, и, особенно, его конструктивные комментарии. Я благодарю моего студента Дэвида Нокса (David Knox), который прочитал черновик этой книги, за его ценные комментарии и за высказывание, что эта книга — ...всё же читабельна. Я пользуюсь случаем поблагодарить моего друга профессора Тома Альтмана (Tom Altman) из Университета Колорадо в Денвере, вдохновляющие идеи и практические советы которого помогли мне значительно продвинуть теорию и приложения LG. Очень важно иметь друга, на которого Вы могли бы положиться в самых трудных ситуациях на работе и в жизни. Я благодарен моему сыну Мише, в настоящее время студенту 1-го курса Стэнфордского Университета, который внёс вклад в развитие LG для агентов с переменной скоростью и разработал удивительную обложку для этой книги. Ещё один человек, которого я хотел бы поблагодарить — это Гарри Фолвен (Gary Folven), мой издатель. Его энтузиазм в связи с изданием этой книги и невероятное терпение помогли мне успешно закончить эту работу. В этом кратком обзоре невозможно перечислить всех, кто внёс вклад в развитие LG. Я хотел бы выразить мою благодарность многочисленным исследователям, инженерам и студентам, интерес и усилия которых помогли прояснить и развить различные аспекты LG. В СССР эти исследования поддерживались грантами от Государственного Комитета по Науке и Технике (ГКНТ) и от Министерства Энергетики (МинЭнерго). Доступ к наиболее современным компьютерам был обеспечен Вычислительным Центром Госплана СССР (ГВЦ Госплана), Всесоюзным Научно-Техническим Информационным Центром (ВНТИЦ) и Вычислительным Центром Коллективного Пользования "Здравоохранение" при Правительстве Москвы (ВЦКП "Здравоохранение"). Много лет дружественная атмосфера интереса и поддержки Всесоюзного Научно-Исследовательского Института Электроэнергетики (ВНИИЭ) помогала мне в развитии LG. В Канаде и затем в США эти исследования на различных этапах поддерживались Национальным Научно-Исследовательским Советом Канады (NSERC) и Мак-Гилльским Университетом, Канада, Офисом Научных Исследований ВВС США (AFOSR), Летней Профессорской Стипендией Лаборатории Военно-Воздушных Сил им. Филипса (Air Force Phillips Laboratory), грантами от Министерства Энергетики через Сандийскую Национальную Лабораторию (Sandia National Laboratories), а также Исследовательскими Стипендиями Университета Колорадо в Денвере. В настоящее время, эти исследования поддерживаются значительным грантом от Агентства Перспективных Исследований Министерства Обороны США (Defense Advanced Research Projects Agency — DARPA). |
|
|
| 1 ВВЕДЕНИЕ |
|
Лингвистическая Геометрия (LG) включает синтаксические инструменты для представления знаний и логического вывода в многоагентных системах, путём моделирования их как абстрактные настольные игры. Инструменты LG позволяют оценить вычислительную сложность и точность решений, а также сгенерировать компьютерные программы для определенных проблемных областей. LG позволяет нам выявить внутренние, скрытые свойства эвристик человека-эксперта, которые продемонстрировали успех в некотором классе игр. Этот подход даёт возможность переносить формальные утверждения и конструкции от одной задачи к другой, т.е. повторно использовать инструменты в новой проблемной области. В некотором смысле, подход на основе LG — это применение метода шахматного эксперта к управлению навигацией робота или календарному планированию ремонтов и наоборот. Что мы знаем о методах шахматного эксперта? Конечно, компьютер — это совершенный инструмент для распознавания и моделирования таких методов. История компьютерных шахмат началась со статьи профессора Клода Шеннона (1950), в которой он предложил общую схему для последующих разработок. Используя, главным образом, поиск решения по методу полного перебора (англ. "брут форс" — грубая сила), т.е. полагаясь, в конечном счёте, на быстродействие компьютеров, шахматные программы постепенно улучшили свой уровень игры (Ньюборн, 1996). В середине 90-х годов, они достигли уровня гроссмейстера. После исторического события в мае 1997 года, когда Дип Блю (Deep Blue — компьютерная шахматная система фирмы IBM) победила чемпиона мира по шахматам Гарри Каспарова, компьютерные шахматы потеряли свою захватывающую привлекательность. В июне 1997 года, профессор Джон Маккарти писал: “В 1965 году российский математик Александр Кронрод сказал, что "шахматы — дрозофила ИИ". Однако компьютерные шахматы разрабатывались так, как могло бы случиться с генетикой, если бы усилия учёных концентрировались, начиная с 1910 года, только на выведении быстрой дрозофилы. Но тогда мы всё же имели бы немного науки, хотя главным образом, мы получили бы очень быстрых плодовых мушек” (Маккарти, 1997). Все самые большие успехи в компьютерных шахматах, включая триумф Дип Блю, были связаны с методом решения "брут форс". Сможем ли мы использовать какие-либо из этих результатов для решения других задач, особенно для задач, имеющих намного большую размерность? Вряд ли. Даже на суперкомпьютерах будущего, мы не сможем решать такие задачи по методу "брут форс". Метод гроссмейстера (т.е. почти без перебора ходов) пока ещё не раскрыт. После события 1997 года стало яснее, чем когда-либо прежде, что шахматы предназначены быть научной дрозофилой ИИ, а не только тестом для проверки скорости компьютеров (Маккарти, 1990, 1997). Однако, не все исследования в компьютерных шахматах проводились в направлении поиска решений по методу "брут форс". В 70-х и 80-х годах в Москве (Россия) разрабатывался проект ПИОНЕР во главе с экс-чемпионом мира по шахматам профессором Михаилом Ботвинником. В своей книге (1984) Ботвинник писал, что метод решения "брут форс" “едва ли способен к дальнейшему прогрессу. Настала очередь принять компьютеру более плодотворный метод, возможно, ПИОНЕР. И, если ПИОНЕР неудачен, то мы должны быть уверены, что другой метод всё же будет найден. Задача должна быть и будет решена”. LG — прямой преемник проекта ПИОНЕР. Дрозофила ИИ “летит через эту книгу, оплодотворяя различные эксперименты и генерируя новые идеи”. Среди других примеров в этой книге мы рассматриваем ряд задач моделирования боя. Это — Рети-подобные задачи, т.е. обобщения знаменитого этюда Рети (Ботвинник, 1979, 1984). Здесь они — называются задачами 2D/4A, 3D/4A, с частично и полностью параллельным моделированием боя. Эти задачи достаточно просты, чтобы использоваться для демонстрации LG-подхода. С другой стороны, они всё-таки не тривиальны и требуют существенного перебора, если их решать с использованием традиционных подходов. Важно общее понимание того, что Рети-подобные задачи являются P-SPACE-полными или, по крайней мере, относятся к группе (или подклассу), так называемых, NP-сложных задач, т.е. таких, для которых не существует алгоритмов, приводящих к решению за полиномиальное время (Гэри и Джонсон, 1991). Инструменты LG позволяют нам решать задачи из этого подкласса и многие другие задачи, используя алгоритмы полиномиальной сложности. Поэтому можно предположить, что Рети-подобные задачи являются представителями более широкого класса задач с низкой (полиномиальной) вычислительной сложностью (т.е. их можно рассматривать и как новый подкласс в группе P-TIME задач). Вероятно, многие важные задачи из реальной жизни, рассмотренные ниже, входят в этот подкласс (Рети-подобных задач). |
|
|
|
Различают классы задач полиномиальной сложности по времени: и по требуемой памяти: где P-детерминированная полиномиальная сложность, а NP-недетерминированная полиномиальная сложность.
Упрощённая классификация задач по вычислительной сложности.
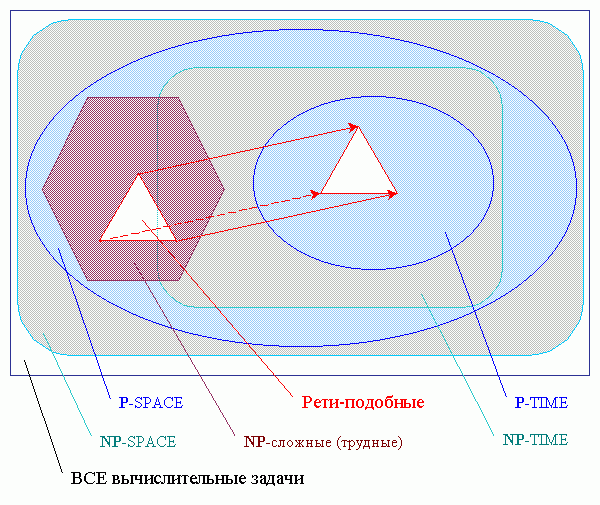
|
|
|
| 1.1 Проблематика |
|
Разработка новых технологий необходима для моделирования различных параллельных многоагентных систем типа операций наземного и воздушного боя, отслеживания и возможного перехвата ракет и спутников, разведывательных операций наблюдения и т.д. Беспилотные самолеты или танки могут участвовать в разведывательных миссиях или в полномасштабной боевой операции. Подобные отряды интеллектуальных транспортных средств могут участвовать и на стороне противника. Управление этими действиями требует постоянной адаптации к промежуточным результатам и динамическому пересчёту в режиме реального времени. Ещё один пример — это задача управления в режиме реального времени воздушным боем, в котором группа самолётов (пилотируемых или беспилотных), оснащённых защитными средствами, уклоняется от группы преследователей, оснащённых ракетами. Другой пример — это задача оптимального управления беспилотными самолётами (UAV), которые барражируют в разведывательном полёте, чтобы определить местонахождение подвижных пусковых установок ракет. Фактические точки запуска ракет обычно обнаруживаются датчиками при помощи спутника. UAV используются для того, чтобы, зная координаты этих точек, найти подвижные установки и, по возможности, уничтожить их. В сценарии из реальной жизни управление UAV нужно рассматривать вместе с воздушным боем, когда UAV уклоняются от преследующих их самолетов врага и, в свою очередь, продолжают поиск подвижных пусковых установок противника. Подобные задачи генерации и перепланирования боевых сценариев в режиме реального времени существенны также для морских и наземных операций. Традиционные модели боевых операций могут быть вычисляемы и даже могут иногда иметь аналитические решения в простых случаях. Однако, в реальных ситуациях при использовании традиционных подходов эти задачи в вычислительном отношении неразрешимы. Задачи моделирования космического боя, в общем-то, подобны другим задачам боевого моделирования. Однако, астродинамика космического корабля делает эти задачи значительно более сложными. Другой фактор — автономность транспортного средства. В то время как автономность наземных, морских и воздушных транспортных средств очень желательна, она просто необходима для космического корабля, особенно если он далеко от Земли. Моделирование и управление боем двух-трёх космических кораблей требует огромного количества вычислений. Задачи с ещё большим числом транспортных средств в вычислительном отношении неразрешимы (Шинар, 1990; Гарсия-Ортиз и др., 1993). Другой класс задач связан с организацией работы интеллектуальных автоматов в индустриальной среде. Группы роботов перемещаются по заводу, комплектуют сборочные детали, подают их на сборочный конвейер и собирают изделие. В результате намеренно локализованного управления, роботы сотрудничают только в пределах своих групп. Различные группы конкурируют друг с другом за общие ресурсы, включая детали, пути движения, очерёдность сборки и т.д. Планирование этих действий требует огромного количества вычислений при использовании традиционных подходов. Задачи конверсии программного обеспечения (ПО) требуют преобразования неструктурированных программ в объектно-ориентированное ПО, причём, иногда требуется, чтобы конечный результат такого преобразования был доказуемо правильной программой. Цель этой конверсии состоит в преобразовании неструктурированного оригинала, так называемого наследуемого ПО, в изделие, которое можно сопровождать (т.е. вносить в него изменения) в течение его жизненного цикла. Этот класс задач может быть сведен к задачам преобразования графа, где первоначальный граф представляет ПО, которое нужно конвертировать. Как правило, для этого используются системы переделки графов (graph-rewriting systems). В то время как ПО небольшого размера конвертируемо, попытка перейти к конверсии реального полномасштабного ПО сталкиваются с непреодолимыми вычислительными трудностями. Задачи безопасности и целостности компьютерных сетей и проблемы кибервойны в Интернете недавно привлекли всеобщее внимание. Вопрос состоит в том, как защитить национальную компьютерную сеть от нападения миллиардов компьютерных вирусов и червей? Какие узлы и даже ветви должны быть отключены ("пожертвованы"), какие из них следует заново подключить ("оживить") путём активизации дубликатов, какие контрмеры должны быть приняты? Традиционный ответ на эту угрозу — локальная защита. Очевидно, что количество вычислений, необходимых для генерации стратегии для глобальной защиты делает эту задачу неразрешимой. Задачи составления расписаний с распределением ресурсов встречаются повсюду. Они включают составление графика различных операций в индустриальной среде в соответствии с очередью заявок и доставку требуемых ресурсов по месту конкретной операции. Обычно, не все заявки могут быть удовлетворены из-за нехватки ресурсов, в то время как число заявок может достигать тысяч. Как выделить самые важные заявки, чтобы получить лучший график? Одна из таких задач — это задача составления графика ремонтов генерирующего оборудования электростанций. Вывод генератора в ремонт требует, чтобы он был остановлен и, следовательно, необходимо компенсировать потерю его мощности из запасов мощности на других электростанциях. Подобные задачи, как известно, в общем случае в вычислительном отношении неразрешимы (Гэри и Джонсон, 1991). Программирование игры в шахматы — это вовсе не обязательно важная для практики, но конечно стимулирующая и трудная задача. Она особенно привлекательна потому, что в отличие от многих других задач в шахматах истинные эксперты действительно существуют — это гроссмейстеры и шахматные чемпионы. Некоторые из них способны к анализу путём самонаблюдения и сравнения своего видения с компьютерными моделями игры. Это даёт нам шанс на успешное распознавание и формализацию их подхода с возможным его использованием в других проблемных областях. |
|
|
| 1.2 Современные Подходы |
|
Задачи планирования ближних и дальних миссий, особенно для автономной навигации, управления космическим роботом (типа UAV), управления операциями космического боя, глобальной и локальной разведки и т.д. обычно описываются математически в форме дифференциальных игр уклонения от преследования. Классический подход, основанный на традиционной теории Дифференциальных Игр (Айзекс, 1965) недостаточен, особенно в случае динамических, многоагентных моделей (Лиров, Родин и др., 1988; Гарсия-Ортиз и др., 1993). Известно, что при классическом подходе существует небольшое количество дифференциальных игр, для которых построены точные аналитические решения. Есть ещё несколько классов дифференциальных игр, для которых численные решения могут быть получены за разумное время при весьма ограничивающих условиях. Однако каждая из этих игр должна быть типа "один против одного", что, естественно, далеко от реальных боевых сценариев. Кроме того, эти игры являются играми с "нулевой суммой", что не позволяют новому агенту "войти" в игру или некоторым агентам обеих сторон быть исключёнными. Другие трудности связаны с потребностью в трёхмерном (пространственном) моделировании с ограничениями на время жизни агентов или с одновременным участием разнотипных агентов, например, поверхностных, подводных или космических транспортных средств. Следуя профессору Родину (Родин и др., 1987, 1988; Родин, 1988; Шинар, 1990) — это может быть реализовано с помощью дискретно-событийного моделирования Сложных Систем управления. Эти методы могут быть основаны на генерации состояний, имеющих геометрический смысл. Конечное дерево игры (ДИ) может быть получено путём дискретизации времени. Узлы дерева будут представлять состояния игры, в которых игроки смогут выбирать своё управление для каждого временного интервала. Также, можно будет определить ходы, соответствующие противоборствующим сторонам (включая одновременные действия). Таким образом, ветви дерева будут представлять последовательности ходов в пространстве игры, а сами задачи могли бы рассматриваться как проблемы планирования в ИИ. Главная трудность — комбинаторный взрыв дерева перебора (ДП). Согласно (Лиров, Родин и др., 1988) “...в случае игры с двумя самолетами задача оптимального выбора не является слишком трудной, так что исчерпывающий перебор в поисках лучшей модели может быть выполнен за разумное время. Однако проблема перебора начинает вызывать особое беспокойство, если вдруг все самолёты примут участие в игре одновременно или, в более сложном примере, когда другие объекты, например препятствия, могут быть введены в игру в будущем”. Как бороться с комбинаторным взрывом? Можем ли мы уменьшить среднее число альтернатив, которые рассматриваются в каждом состоянии (позиции), в конечном счёте, доведя их до одной альтернативы? Идеальным был бы алгоритм, способный найти решение вообще без перебора на дереве ходов. Пусть коэффициент ветвления B — параметр, представляющий среднюю ширину ДП в каждом узле. Он показывает, сколько ветвей (ходов) в среднем должно выходить из каждого узла ДП. Например, в шахматных программах, использующих алгоритмы перебора по методу "брут форс", в каждом узле рассматриваются все возможные ходы (т.е. разрешённые в позиции шахматными правилами). Это означает, что мы должны генерировать ДП с числом узлов T, которое может быть рассчитано по формуле (1.2.1). В этом уравнении B — среднее число ходов из каждой позиции, L — глубина перебора (предполагается, что все ветви усечены до глубины L) и T — общее количество построенных позиций (узлов). Вычисление B основано на рассмотрении гипотетического ДП с глубиной всех ветвей равной L, общим количеством узлов равным T при постоянном числе потомков у каждого узла. По определению (Нильсон, 1980; Рич и Найт, 1991) это постоянное число равно коэффициенту эффективного ветвления B и определяется как решение уравнения (1.2.1) для заданных L и T относительно B. Большие значения B соответствуют неизбирательному перебору. Очевидно, что большое значение B указывает на рост ДП по экспоненциальному закону с большим основанием степени. Алгоритмы, которые уменьшают B, особенно те алгоритмы, которые делают B близким к 1, нужно рассматривать как наилучшие, направленные "прямо" к цели, с минимальным ветвлением в других направлениях. Используя уравнение (1.2.1) для значения T — общего количества узлов, которые фактически построены в процессе перебора и значение L — требуемой глубины перебора, мы можем вычислить коэффициент ветвления B для произвольного переборного алгоритма. Коэффициент эффективного ветвления B можно найти как аппроксимацию решения уравнения (1.2.2) относительно B. Это нелинейное уравнение и его можно решить различными методами, включая метод проб и ошибок. |
| B + B2 + ... + B L = T | (1.2.1) |
| или | |
|
B L+1 - 1 ————— = T . B - 1 |
(1.2.2) |
|
Для уменьшения коэффициента ветвления были разработаны различные переборные алгоритмы типа динамического программирования и метода ветвей и границ. Для антагонистических игр двух игроков (типа шахмат) самые популярные алгоритмы — это различные алгоритмы перебора с формальным альфа-бета отсечением (Нильсон, 1980; Рич и Найт, 1991). Они реализованы в самых сильных шахматных программах, включая действующих и экс-чемпионов мира по компьютерным шахматам. Было доказано, что в лучшем случае алгоритм альфа-бета перебора может уменьшить число терминальных узлов в дереве перебора следующим образом (Слэйгл и Диксон, 1969; Кнут и Мур, 1975):
Это число узлов должно быть просмотрено в любом случае, даже при оптимальном упорядочении ходов. Все различные модификации альфа-бета перебора не могут улучшить этот результат (Кэйндл, 1990). Однако, при альфа-бета переборе число узлов ДП растёт всё ещё по экспоненциальному закону, хотя и с меньшим основанием. Теоретически при альфа-бета отсечении на ДП можно удвоить глубину перебора (за то же самое время счёта), если оптимально упорядочить ходы в узлах ДП. Это упорядочение приводит к уменьшению коэффициента ветвления примерно до √B. В этой книге мы используем √B, как значение уменьшенного коэффициента ветвления, в нашем сравнении результатов альфа-бета перебора, получаемых в самом благоприятном случае, с результатами применения средств LG. Предположим, что произвольная шахматная позиция в среднем содержит примерно 40 ходов по правилам, тогда альфа-бета отсечение может уменьшить это число примерно до 6 (≈√40). Однако мы всё ещё имеем рост по экспоненциальному закону с очень большим основанием степени B=6 (т.е. коэффициентом ветвления). В результате, шахматные задачи, которые требуют глубокого перебора, например до глубины L=20 или больше ходов, требуют и огромного количества времени для получения решения. Даже специализированная программно-аппаратная система Дип Блю не способна преодолеть это препятствие (Хсу и др., 1990; Ньюборн, 1996, 1997). Эта массово-параллельная система из шахматных чипов специального назначения со скоростью вычислений до двухсот миллионов позиций в секунду не способна противостоять росту ДП по экспоненциальному закону с большим коэффициентом ветвления. В задачах из реальной жизни число альтернатив намного больше 40, в то время как требуемая глубина перебора может превышать сотни ходов. Даже суперкомпьютеры будущего не смогут произвести такое количество вычислений при использовании традиционных процедур перебора по методу "брут форс". Один из основных подходов к сокращению перебора — это метод уменьшения размерности Сложной Системы путём её декомпозиции на меньшие подсистемы, используемый экспертами в различных областях. Процесс декомпозиции может быть применён рекурсивно, пока мы не получим группу базовых подзадач, которые можно рассматривать (в некотором смысле) независимо друг от друга. Всё это сродни планированию в присутствии подцелей, макрооператоров и абстракций (Корф, 1987; Тэйт, Хендлер и Драммонд, 1990). На каждом уровне декомпозиции мы можем применять абстракцию, т.е. первоначально игнорировать детали низкого уровня и сконцентрироваться на существенных особенностях задачи, а к деталям мы сможем вернуться позже. В некотором смысле, эксперты обычно устанавливают подцели (и достигают их), потому что они знают какую последовательность операторов (т.е. макрооператор) применить, чтобы дойти до следующей подцели. Идея абстракции при решении задач человеком была указана в работе (Пойа, 1945), позже она использовалась в версии Универсального Решателя Задач (GPS), предназначенной для планирования (Ньюэлл и Саймон, 1972). С тех пор подобные идеи были применены во многих системах в рамках формальных теорий линейного и нелинейного планирования (например, Сакердоти, 1974, 1975; Штефик, 1981; Чэпман, 1987; Кноблок, 1990; Георгев, 1990; Мак-Аллистер и Розенблит, 1991) или в рамках других подходов (Месарович и Такахара, 1989; Эльбас, 1991). Реальные Сложные Системы обычно включают динамические процессы, которые не подконтрольны одиночному агенту. Решатель задач должен учитывать действия, неподконтрольные данному агенту, которые могут производиться последовательно или параллельно с его действиями. Различные теории планирования для многоагентных систем были предложены в работах (Аллен, 1984; Георгев, 1983, 1990; Мак-Дермот, 1985; Пелевин и Аллен, 1986). В частности, можно рассмотреть обобщённый тип события как множество последовательностей состояний, представляющее все варианты появления этого события во всех возможных ситуациях, которые могли бы включать и параллельные действия многих агентов. Один из возможных подходов — это аппроксимация параллельных действий с использованием взаимного чередования (одновременных ходов) или интерливинг-приближения (Георгев, 1983; Педнаулт, 1987). Мы используем аналогичное приближение в наших примерах в главах 3, 4, 5 и 6. Конечно, в рамках этого подхода нельзя моделировать одновременные события; для этого мы вводим истинный параллелизм (Штильман, 1995d, 1997a; Скисов и Штильман, 1997, 1998a, 1998b; и глава 6). Помимо множества специфических проблем, включая неопределённость, свойственную принятию решений для данного агента из-за одновременных действий других агентов, для одноагентных систем всё же остаётся основная проблема планирования, которая ещё и значительно усиливается при многих агентах. Это проблема комбинаторного взрыва пространства перебора. Представление параллелизма в виде ходов, включающих все одновременно допустимые комбинации действий, приводит к огромному росту коэффициента ветвления и, следовательно, к росту пространства перебора (главы 6, 13 и 14). Ни один из традиционных подходов к задачам, которые рассмотрены в разд.1.1, не может быть масштабирован (для применения в реальных параллельных системах) по отношению к числу агентов, динамическому изменению их возможностей, их величины и формы, размерности их операционной области, к их параллельным действиям, к требованиям режима реального времени и т.д. Одна из главных трудностей — это огромная сложность вычислений из-за экспоненциального роста числа вариантов, которые должны быть проанализированы. К счастью, есть много проблемных областей, в которых способности экспертов к логическому выводу в многоагентных Сложных Системах несравненно сильнее, чем уровень современных компьютерных систем (если мы ведём речь о сокращении сложности). Хотя и нет никаких гроссмейстеров в боевом моделировании или в управлении навигацией робота, но в шахматной игре гроссмейстеры достигли удивительных результатов в сокращении перебора. Наша цель состоит в том, чтобы изучить методы эксперта при принятии решений в областях, где они приводят к успеху, чтобы обнаружить причины этого успеха, формализовать их и затем применить эти формализмы к новым, пока еще нерешённым задачам. Как уже говорилось, одна из главных эвристик перебора, используемых экспертами, связана с декомпозицией системы на подсистемы. Декомпозиция была осуществлена для многих классов задач с различными результатами. Реализации, основанные на формальных теориях линейного и нелинейного планирования, сталкиваются с проблемами эффективности. Эффективный планировщик требует интенсивного использования эвристических знаний. С другой стороны, чисто эвристическая реализация специфичная для одной области, едва ли может быть воспроизведена в других проблемных областей. Каждая новая задача требует тщательного изучения, а предыдущий опыт обычно не может быть использован. Существует ли общий конструктивный подход для выхода из этого тупика? Каковы формальные свойства экспертных эвристик, которые привели нас к успешной иерархии подсистем в данной задаче? Как применить те же самые идеи в другой проблемной области? Нам потребуются формально-языковые средства для адекватного представления навыков экспертов. Применение таких средств в области, где эксперты уже достигли успешных результатов, должно привести к разработке формальных знаний, независящих от проблемной области, которые можно будет применить в других областях. Ни естественные языки, ни языки программирования не удовлетворяют этой цели. Первые — неформальны и неоднозначны, в то время как вторые — обычно чересчур детализированы средствами низкого уровня. Мы должны понять, как формально представить, сгенерировать и исследовать математическую модель, основанную на абстрактных образах, извлекаемых из видения задачи экспертом. |
|
|
| 1.3 LG с первого взгляда |
|
Лингвистическая Геометрия (LG) включает синтаксические инструменты для представления знаний и логического вывода в многоагентных Сложных Системах. LG была разработана как общий подход для некоторого класса Сложных Систем. Этот подход предоставляет мощные инструменты для сокращения перебора в различных задачах путём декомпозиции Сложной Системы в динамическую иерархию взаимодействующих подсистем. LG позволяет изучать эту иерархию формально, исследуя её общие и специфические свойства. LG-инструменты предоставляют методику для оценки сложности и точности решений, а также для разработки компьютерных программ — приложений LG к различным прикладным областям. Цель LG состоит в том, чтобы решать разнообразные задачи с огромными пространствами состояний при условии, что мы ищем "по возможности оптимальное или лучшее" поведение агентов, которые генерируют целенаправленные переходы из одного состояния в другое. К таким задачам относятся сотрудничество или противоборство команд интеллектуальных (или управляемых человеком) роботов (т.е. сухопутных или морских транспортных средств, самолётов или космических кораблей); критичные к безопасности системы управления удалёнными автоматическими объектами, подобные тем, что используются для исследования других планет; проектирование VLSI; долгосрочное планирование, составление расписаний и распределение ресурсов; шахматы и т.д. Традиционно, поиск оптимального или почти оптимального поведения объектов для вышеупомянутых систем требует полного перебора ветвей в гигантском дереве перебора (ДП). Такой перебор часто превышает (по ресурсам времени и памяти) возможности современных и даже мыслимых компьютеров будущего. LG-подход существенно уменьшает размер ДП, делая задачи решаемыми. Хотя дискретность заложена в природе LG, этот подход может быть применён и к управлению непрерывными процессами, которые описываются обыкновенными дифференциальными уравнениями или уравнениями в частных производных после их дискретизации. Одна из уникальных особенностей подхода на основе LG — это формализация и использование эвристик перебора, разработанных высоко квалифицированными экспертами (включая шахматных гроссмейстеров). Эти эксперты разработали сложные, но очень удачные стратегии, приводящие к значительному сокращению перебора в соответствующих областях. Однако, до публикации этой работы эвристические методы и интуиция экспертов, связанных с переборными задачами, были непонятны ни специалистам по ИИ, ни самим экспертам. Основываясь на теории формальных языков, геометрическом подходе и мощном аппарате современной формальной логики, мы формализовали и обобщили экспертные эвристики, сделав их применимыми к обширному классу задач. До появления LG большинство задач этого класса, как полагали сами эксперты, не находилось в областях применимости их эвристик. Результаты сравнения LG-подхода с другими методами приведены на рис.1.1. Показаны три различных ДП. Верхний треугольник обозначает дерево, которое будет построено при использовании перебора по методу "брут форс". Широта этого дерева отражает высокий коэффициент ветвления. Однако, поскольку время ограничено, все ветви должны быть прерваны на небольшой глубине (например, на одной и той же). Дерево, построенное с применением алгоритма альфа-бета перебора, является более глубоким и более узким. Это — результат отсечений, которые позволяют уменьшить коэффициент ветвления и строить более глубокие ветви за то же самое время. Доказано, что оптимальная ветвь не будет отсечена, она будет той же, как в случае перебора по методу "брут форс" с такой же самой глубиной (Кнут и Мур, 1975). Однако, даже в этом случае рост перебора по экспоненциальному закону с большим основанием степени (коэффициентом ветвления) не позволяет нам решать большинство задач из реальной жизни. Третье, очень узкое и глубокое дерево отражает то, что при переборе на основе LG коэффициент ветвления равен точно 1 или близок к 1. Было также доказано, что для некоторого класса задач LG-алгоритм — это оптимальная (выигрышная или ничейная) стратегия (глава 13). |
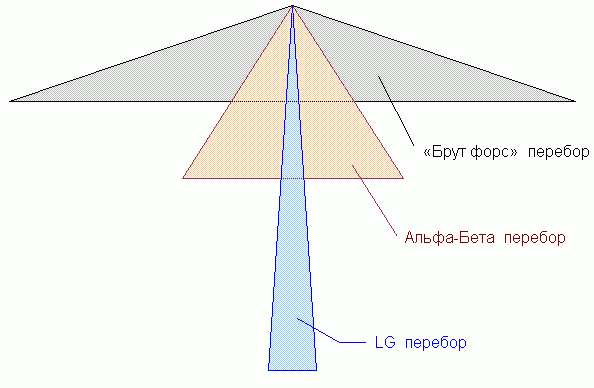
Рис.1.1 Сравнение деревьев перебора для трёх типов перебора за одинаковое время вычислений. |
|
Подход на основе LG применим к параллельным многоагентным системам. Что это за агенты? Введём агентов двух типов. Агенты высшего уровня — это суперагенты, способные к действию посредством некоторого числа подвижных объектов, т.н. локальных агентов. Окружающая среда может оказывать существенное воздействие на движение агентов. Одни пункты операционной области могут быть достижимы за некоторое число ходов, другие могут быть вовсе не достижимы. Рассмотрим системы с двумя суперагентами, которые действуют друг против друга. Они называются противоположными сторонами. Обычно эти суперагенты преследуют противоположные цели. Каждый из них управляет командой локальных агентов, чья свобода действий существенно ограничена. В конечном счете, в примерах, рассмотренных в этой книге, локальные агенты вовсе не имеют свободы и полностью контролируются суперагентом. Однако, инструменты LG применимы и к тем моделям, в которых локальные агенты менее ограничены и работают независимо по своему разумению. Каждый суперагент разрабатывает модель своего оппонента, предполагая, что тот будет действовать наилучшим образом в рамках этой модели. Модель используется, чтобы планировать действия суперагента и выбирать оптимальные. Модель устанавливает локальные цели для локальных агентов. Эти локальные цели скоординированы с глобальной целью соответствующего суперагента. Движения, направленные к локальным целям, связаны со стремлением суперагента достигнуть своей глобальной цели. Модель является динамической, т.е. после каждого действия, которое может включать и одновременные передвижения агентов обеих сторон, она обновляется с учётом новой ситуации. Динамическая модель может рассматриваться как иерархия подсистем. Мы вводим локальные цели, разбивая систему локальных агентов на подсистемы, которые стремятся к достижению своей цели. Например, каждая подсистема второго уровня включает локальных агенты обеих противоположных сторон: цель одной стороны состоит в том, чтобы атаковать и уничтожить локального агента другой стороны (мишень), в то время как противоположная сторона старается его защитить. Например, в управлении навигацией робота это означает, что выбирается пара роботов противоположных сторон: один — как нападающий элемент, другой — как локальная мишень. Затем генерируются локальные пути, ведущие к мишени, а также пути других роботов, поддерживающих нападение или защищающих мишень. Иерархия подсистем в LG представлена как иерархия формальных языков. Чтобы ввести формальные языки, следуя (Хопкрофт и Ульман, 1979), мы должны использовать символы. Символ — это абстрактный объект, который мы не будем сейчас определять формально. Примеры символов включают a, t, a(xi), t(p2, t2, τ2), π(i5) и т.д. Цепочка символов (или слово) — это конечная последовательность символов, записанных рядом друг с другом. Например, a(x1) a(x2) ... a(xn) — это слово, если a(x1), a(x2), ... , a(xn) — символы. Алфавит — это конечное множество символов. Формальный язык — это множество слов, состоящих из символов некоторого алфавита. Тогда пустое множество и множество {e}, состоящее из пустого слова e — это языки. Рассмотрим язык W и слово w этого языка. Алфавит V(w) слова w является множеством символов, элементы которого, по крайней мере, однажды встречаются в слове w. Например, множество
V={ a(x1), a(x2), ... , a(xn) }
- это алфавит слова a(x1) a(x2) ... a(xn). Диаграмма Иерархии Формальных Языков показана на рис.1.2 в виде множества треугольников трёх типов. Любое состояние из пространства состояний (т.е. из множества всех позиций или из всех возможных конфигураций агентов на абстрактной доске) представлено иерархией из двух вложенных треугольников (Языка Траекторий и Языка Сетей Траекторий). Несколько треугольников, которые представляют состояния (вместе с их двойной иерархией и дополнительными атрибутами), вложены в один большой треугольник — слово Языка Переводов. Этот высокоуровневый язык собственно и включает в себя решение задачи. Детальное описание Иерархии Языков в LG начинается в главе 2 и продолжается в главах 8-12. Более точная (но сложная) версия этой диаграммы показана на рис.1.4. Ниже, мы даём предварительное, краткое введение в эту Иерархию. |
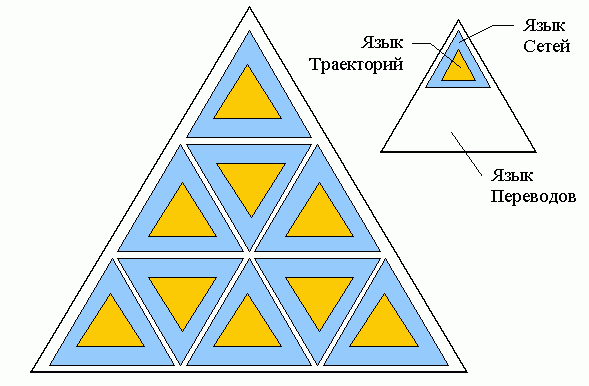
Рис.1.2 Иерархия подсистем в LG как Иерархия Формальных Языков. |
|
Подсистемы первого уровня в LG представлены Языком Траекторий, который является множеством "траекторий", т.е. слов типа:
где xi — называются параметрами. Значения параметров определяются семантикой проблемной области. Слова этого типа представляют пути (траектории) локальных агентов. Например, для модели роботов xi — координаты планируемого пути робота. Подсистемы второго уровня в LG представлены Языком Сетей Траекторий, который является множеством Web-сетей, т.е. слов типа:
где pi, ti, τi — называются параметрами; pi — это локальный агент системы (робот или программный агент), ti — это траектория агента pi, а τi является списком параметров, зависящих от конкретной задачи. Эти Web-сети представляют рабочую схему для локального динамического планирования. Агенты перемещаются по траекториям, стремясь к достижению своих локальных целей, в то время как суперагент продвигается к глобальной цели, типа победы в бою или лучшего графика ремонтов электрогенераторов. Наша система может иметь несколько уровней для языков Web-сетей, представляющих иерархию подсистем. Полная система функционирует, переходя из одного состояния в другое, т.е. движение локального агента из одного пункта в другой вызывает изменение иерархии языков. Это изменение можно представить как отображение, т.е. перевод из одной иерархии языков в другую или, более точно, в новое состояние той же самой иерархии. При переборе ходов в поисках оптимальной стратегии мы генерируем множество путей (последовательностей ходов) в пространстве состояний; таким образом, этот перебор можно рассматривать как последовательность переводов иерархии языков. В LG в формальном языке высшего уровня — Языке Переводов — любой перебор представлен словом:
где ik — называются параметрами. Каждый символ π(ik) соответствует ходу локального агента по Web-сети. Перебор (вывод слова) на Языке Переводов представляется фактически как поиск оптимальной или близкой к оптимальной стратегии типа выигрышной стратегии для боя, лучшего графика ремонтов и т.д. Вывод слова в этом языке управляется взаимодействием всех Web-сетей. Результат вывода — существенно уменьшенный перебор, который и приводит к решению задачи. |
|
|
| 1.4 Углублённое рассмотрение LG-подхода |
|
Классы задач, которые будут изучены — это задачи оптимального управления LG-системой, т.н. Сложной Системой. Эта система определена (ОПРЕДЕЛЕНИЯ 2.1-2.4) как пара множеств: множество точек (пунктов) и множество локальных агентов, которые перемещаются, двигаются из одной точки в другую. Это — очень общее представление. Например, в задачах управления навигацией робота локальные агенты — это автономные роботы, перемещающиеся по траектории (построенной из точек) в сложной и опасной двумерной или трёхмерной окружающей среде. Агенты могут быть разделены на две или более противоположные стороны (т.е. на суперагентов), хотя в этой книге мы рассматриваем только системы с двумя сторонами. Каждая сторона может атаковать, уничтожать агентов противника и защищать своих агентов. Уничтоженный агент должен быть удален из системы, но он может появиться вновь в другой ситуации. Удаление происходит, когда атакующий агент перемещается в точку, где уже стоит агент противника. Каждая сторона стремится достичь множества определённых позиций — конфигураций агентов. Например, подобная конфигурация может представлять множество точек, в которых расположены агенты обеих сторон, с максимальным выигрышем, т.е. величина алгебраической суммы стоимостей своих и чужих агентов, которые уничтожены (и удалены из системы) достигла максимума. LG-система работает, переходя из одного состояния в другое, т.е. ход игрока в виде перемещения агента (одной стороны) из одной точки в другую приводит к переходу системы из текущего состояния в другое состояние. Например, множество желательных конфигураций агентов можно рассмотреть как множество целевых состояний. Любое состояние может быть описано списком агентов и их местоположением. С каждым состоянием LG связывает иерархию структур. Состояние характеризуется структурой Траекторий, которые являются возможными путями движения агентов, присутствующих в этом состоянии. Каждое состояние также характеризуется структурой Зон, которые представляют все области локального боя в этом состоянии LG-системы. Структура Зон основана на структуре Траекторий и является более сложной, чем структура Траекторий. Таким образом, LG рассматривает структуру Зон как стоящую выше в иерархии, чем структура Траекторий. Иерархия структур была построена на основе иерархии подсистем, введенных высококвалифицированными экспертами. Иерархия подсистем была введена следующим образом: одноуровневая LG-система с глобальными целями (по одной для каждой стороны) была заменена многоцелевой, многоуровневой системой путём введения промежуточных целей и разбиения (декомпозиции) полной системы на подсистемы, которые стремятся их достичь. Цели для подсистем различны, но подчинены общей главной цели. Например, каждая подсистема второго уровня, называемая Зоной, включает элементы двух противоположных сторон. Цель одной стороны состоит в том, чтобы напасть и уничтожить мишень, в то время как другая сторона пытается её защитить. В задачах управления навигацией робота это означает, что выбирается пара роботов противоположных сторон: один — как атакующий агент, а другой — как локальная мишень, затем генерируется путь, ведущий к мишени, а так же пути других роботов, поддерживающих атаку или защищающих мишень. Иерархия структур представлена в LG как Иерархия Формальных Языков, где каждое слово языка низкого уровня соответствует одному символу в слове языка более высокого уровня (разд.1.3). При LG-подходе каждая подсистема первого уровня представлена как слово или цепочка символов:
где символы a(xi) взяты из алфавита символов { a(xi) }. Символ a не несёт смысловой нагрузки. Он предназначен для связи параметров xi в одно слово и указания, что это слово — траектория. Значения параметров xi определяются семантикой проблемной области. Слова типа (1.4.1) образуют Язык Траекторий (ОПРЕДЕЛЕНИЕ 2.8). Например, для задачи управления навигацией робота xi — это координаты пунктов остановки в планируемом пути робота. Для задачи составления графика ремонтов аналогичное слово представляет собой вариант графика ремонта для определенного агрегата, причём x1, x2, ... , xn соответствуют определённым дням в составленном графике. Различные типы траекторий определены в разделе 2.4. Подсистема второго уровня представлена также как слово или цепочка символов с параметрами, т.е. в виде Web-сети:
где символ t подобно a в (1.4.1) не несёт смысловой нагрузки. Он предназначен для связи параметров в одно слово и указания, что это слово — Web-сеть. Значения параметров (pi, ti, τi) определяются семантикой проблемной области и подсистем более низкого уровня. Символы pi обозначают агентов нашей LG-системы (роботы, агрегаты и т.д.); символы ti — обозначают Траектории (подсистемы низшего уровня) агентов pi, т.е. слова вида
включённые в эти подсистемы; а символы τi — обозначают время, выделенное для движения по траектории ti. Используя слова (1.4.1), мы можем представить пути агентов LG-системы, а слова (1.4.2) — это Web-сети из некоторых путей, объединенных общей целью. Например, в управлении навигацией робота подобная сеть планируемых путей может моделировать набросок оперативного плана для достижения локальной цели в опасной окружающей среде (с подвижными и неподвижными препятствиями). В задаче составления расписаний это соответствует графику ремонта некоторого агрегата, включая график доставки ресурсов. Множество слов (1.4.2) — называют Языком Web-сетей (ОПРЕДЕЛЕНИЕ 2.18). Различные типы Web-сетей, так называемых Зон, определены в разделе 2.6. Переход к другому состоянию LG-системы приводит к перестройке иерархии структур. Эта перестройка может быть представлена как отображение (перевод) в иерархию структур другого состояния. Фактически, мы можем представить изменение иерархии при переходе LG-системы из одного состояния в другое так, как будто сама иерархия структур изменяет своё состояние. Это означает, что структуры Траекторий и Зон для соответствующих состояний LG-системы образуют состояния иерархии структур. Направленный граф переходов состояний LG-системы порождает граф переходов состояний у иерархии структур. В LG введен ещё более высокий уровень иерархии структур, который является общим для всех состояний. Эта структура высокого уровня представляет поддерево игры (с узлами, соответствующими состояниям LG-системы), которое порождается LG-стратегией игрока при поиске очередного хода в игре. Эту структуру называют деревом LG перебора (или LG-деревом). LG-дерево включает все варианты игры, которые LG-алгоритм генерирует в том состоянии игры, в котором игрок должен сделать ход. LG-дерево включает очень маленькое подмножество вариантов в противоположность полному дереву игры (ДИ). Ограничим употребление термина LG-дерево обозначением поддерева ДИ, представляющего варианты, рассмотренные при вычислении хода игрока в исходном состоянии LG-системы. LG-дерево включает последовательности ходов, т.е. переходов между состояниями LG-системы. Поэтому, мы можем ввести другое дерево — соответствующих последовательностей отображений или переводов Иерархии Языков (которые представляют эти состояния). Существует взаимно однозначное соответствие между этими деревьями. Таким образом, мы будем говорить об одном и том же дереве, называя его деревом ходов или деревом переводов. Это дерево представлено как слово, символы которого соответствуют рёбрам дерева, занумерованным, например, в соответствии с порядком обхода дерева по методу сначала вглубь: π(i1) π(i2) ... π(in) в (1.4.3). Это дерево, в свою очередь может быть записано как пара, состоящая из слова, упомянутого выше, и кортежа функций, которые генерируют потомков в любом узле дерева. Кортеж функций включает тройку функций, которые генерируют крайнего левого потомка, родного брата крайнего левого потомка и их родителя для любого узла дерева. Мы предполагаем, что генерация (обход) дерева происходит слева направо. Этот кортеж описывает сигнатуру, которая задаёт алгебраическую структуру дерева посредством функций, генерирующих потомков (ОПРЕДЕЛЕНИЕ 2.26). Рассмотрим следующие слова:
где каждый символ π(ik) представляет одновременно следующие три понятия: - ребро (дуга) LG-дерева; - ход; - соответствующий перевод. |
|
Слово (1.4.3) — это элемент формального языка высшего уровня — Языка Переводов (разд.2.8 и глава 12). Как и ранее, символ π не несёт смысловой нагрузки. Он предназначен для связи параметров в одно слово и указания, что это слово — дерево переводов. Параметры ik идентифицируют рёбра дерева. Список функций, называемый functions, отражает связи между рёбрами. Эти связи предназначены для поддержки структуры данных дерева, которая представлена здесь линейно как слово или цепочка символов. Построение LG-дерева (1.4.3) управляется генерацией и взаимодействием Web-сетей (1.4.2) и Траекторий (1.4.1). Если LG-алгоритм используется обоими игроками, то вариант (или варианты) ходов, порождаемый применением LG-стратегии для обоих игроков, является некоторой ветвью LG-дерева. Однако этот вариант не обязан быть подсловом (1.4.3) в Языке Переводов, состоящим из непрерывной подцепочки символов. Например, рассмотрим дерево с 4 узлами π(1) π(2) π(3) (рис.1.3). Ребро π(1) ведёт от корня R к единственному потомку, который обозначен как X, ребро π(2) ведёт к левому потомку X и ребро π(3) ведёт к правому потомку X. При обходе сначала вглубь (слева направо) рёбра будут занумерованы в виде списка π(1) π(2) π(3). Подслово π(1) π(2) представляет левую ветвь дерева. Есть ещё одна ветвь, состоящая из последовательности рёбер π(1) и π(3), т.е. подслово π(1) π(3). Однако это подслово π(1) π(3) не является непрерывным подсловом для π(1) π(2) π(3). |
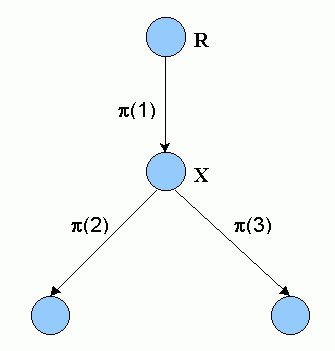
Рис.1.3 Дерево с 4 узлами π(1) π(2) π(3). |
|
Если LG-алгоритм используется только одним игроком, то вариант игры, возникающий после применения LG-стратегии для этого игрока, не обязан быть ветвью LG-дерева, упомянутого выше. Причина состоит в том, что противник может использовать ходы, которые не входят в варианты, образующие LG-дерево. Поскольку LG-алгоритм искушён в отборе вариантов, то те ходы противника, которые не принадлежат этим вариантам, обычно будут более слабыми ходами. Однако, определить слабость ответа противника LG-алгоритм может лишь после построения нового LG-дерева для состояния, которое возникнет после этого неожиданного хода противника. |
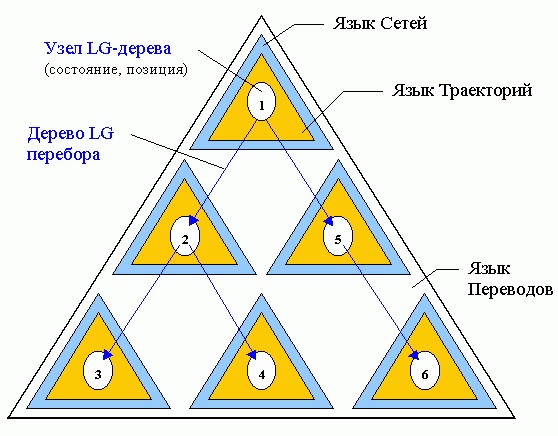
Рис.1.4 Диаграмма Иерархии Формальных Языков в LG. |
|
Диаграмма Иерархии Формальных Языков в LG показана на рис.1.4. Эта диаграмма является детализацией диаграммы, показанной на рис.1.2. Язык Переводов — это язык деревьев перебора. Слово этого языка может быть иллюстрировано деревом. Одно из таких деревьев с 5 рёбрами и узлами (1-6) показано на рис.1.4. Узел этого дерева соответствует состоянию сложной системы (1-6). Декомпозиция системы на подсистемы представлена в LG как Иерархия Формальных Языков. В каждом состоянии декомпозиция представлена иерархией двух языков — Языка Web-сетей и Языка Траекторий. Слово Языка Траекторий соответствует символу в слове Языка Web-сетей. Эта двойная иерархия иллюстрируется двумя вложенными треугольниками, присоединёнными к каждому узлу LG-дерева. Связь между этой иерархией и вышестоящим Языком Переводов (показанным как один большой треугольник) отличается от связи между языками внутри двойной иерархии. Слово Языка Переводов, т.е. перебор, представляет LG-дерево с узлами-состояниями, за которыми закреплены двойные иерархии. Поэтому, двойные иерархии соответствуют каждому символу слова Языка Переводов. Это иллюстрируется на рис.1.4. LG-перебор может быть представлен как логический вывод слова (генерация LG-дерева) в Языке Переводов. Преимущества представления декомпозиции LG-системы в виде Иерархии Формальных Языков станут более очевидными, когда мы рассмотрим формальный механизм для генерации этой Иерархии. В задачах распознавания образов формально-лингвистический подход был предложен для представления иерархически структурированной информации, содержащейся в каждом образе, т.е. для описания образов посредством более простых подобразов. Этот подход обнаруживает аналогию между иерархической структурой образов и синтаксисом формальных языков. Правила, управляющие слиянием подобразов в образы, обычно задаются грамматиками описания образа, а мощь такого описания объясняется рекурсивной природой грамматик. Используя подобный подход для генерации Траекторий и Сетей Траекторий, мы используем раздел теории формальных грамматик, который был разработан Кнутом (1968), Розенкранцем (1969), Волченковым (1979), Штильманом (1985) и называется теорией управляемых грамматик. Детальный анализ управляемых грамматик и их приложений к LG приведен в главах 8-12, 14. Недавнее исследование точности решений, полученных с помощью LG-алгоритмов, привело к более глубокому пониманию мощи этого подхода. Как выяснилось, инструменты LG способны реализовать конструктивную декомпозицию пространства состояний (глава 13). LG-инструменты позволяют нам формально описывать существенные подмножества пространства состояний и формулировать потенциально выигрышные стратегии, т.е. классы путей в пространстве состояний, ведущие из начального состояния в подмножества состояний, которые мы хотим достичь. Некоторые из этих стратегий могут быть забракованы, как нереализуемые. Следующий шаг — это попытка формальной реализации незабракованых стратегий для каждой из противоположных сторон. Это доказуемо лучшее поведение из того, что каждая сторона в принципе может сделать. Применение потенциально выигрышной стратегии для каждой стороны кончается генерацией LG-дерева, которое является оптимальным решением переборной задачи. Подобные идеи работают для различных классов игр. Оптимальность доказана для классов многоагентных последовательных и параллельных военных игр с d-мерной операционной областью действий — подмножеством Zd. Это исследование привело к новому направлению в LG: решение переборных задач путём построения стратегий без какого-либо перебора на дереве (глава 13). |
|
|
| 1.5 LG-стратегии и Теория Игр |
|
Рассмотрим связь между стратегиями Теории Игр и LG-стратегиями (в LG-системе из двух взаимодействующих суперагентов). Теория Игр появилась в 1930-х годах, например (Дж. фон Нейман и Моргенштерн, 1944; Оуэн, 1982) и описана в обширной литературе. Хороший обзор сделан в (Льюс и Райфа, 1957). Важный раздел Теории Игр посвящён моделированию экономического поведения. В этом разделе цели игроков сформированы с помощью функции выигрыша и требования максимизировать вознаграждение игрока. Хотя LG использует оценочную функцию, которая является формой вознаграждения, по духу LG всё же ближе к другому разделу Теории Игр, который был основан в работах (Гэйл и Стюарт, 1953) и называется теорией (бесконечных) игр 2-х лиц с полной информацией. Цели игроков в играх 2-х лиц формулируются посредством множеств желательных вариантов действий, называемых победительными множествами. Выигрышная стратегия для игрока — это такое поведения, которое приводит игрока к победе независимо от того, как ведёт себя противник. Методы построения таких стратегий отличаются от методов Теории Игр, в которых моделируется экономика, тем, что они используют методы логики, алгебры и топологии в отличие от методов математического или функционального анализа и/или вариационного исчисления, применяемых в классической Теории Игр. Методы, подобные вариационному исчислению также используются в другом разделе Теории Игр, который называется Дифференциальными Играми (Айзекс, 1965) — раздел 1.2. Игры Гэйла-Стьюарта (2-х лиц с полной информацией) были расширены до игр на графах в работах (А.Яхнис и В.Яхнис, 1993; Зейтман, 1994). Самая ранняя ссылка на игры на графах содержится в классических статьях по Теории Игр (Кун, 1953; Берж, 1957). В 1993-94 годах было сделано следующее расширение класса игр на графах, позволившее включить параллельные ходы, а также игры с более чем двумя игроками (В.Яхнис и Б.Штильман, 1995b). Введенный класс игр наиболее близок к абстрактным настольным играм (ABG) или Сложным Системам, которые моделируются LG-системой. Цели игр на графах и цели в LG не идентичны, так как в рамках LG-подхода класс полезных стратегий шире, чем класс выигрышных стратегий. Интуитивно, специфические LG-стратегии можно рассматривать как стратегии типа "лучшие из возможных", а не как исключительно выигрышные стратегии. Действительно, часто LG-игры не имеют "детерминированной" выигрышной стратегии из-за параллельных ходов. В результате методы LG приводят к новым способам построения выигрышных стратегий. LG генерирует выигрышные стратегии на основе математических конструкций, которые были впервые введены в LG и приспособлены для формализации стратегий экспертов. Для проведения параллелей нам будет удобно рассматривать LG-систему как игру 2-х лиц, где стороны (или суперагенты) — это игроки. Мы свяжем понятие LG-стратегии для стороны или суперагента со стратегией игрока в игре 2-х лиц. Как обычно, большинство построений для игр 2-х игроков в Теории Игр основано на понятии дерева игры (ДИ). Это дерево состоит из всех возможных ходов игроков и охватывает все возможные варианты розыгрышей в игре. LG связывает с каждым узлом ДИ состояние игры. Состояние игры — это позиция на доске для игр типа шахмат, шашек, крестиков-ноликов и т.д. Для LG-систем (как определено в разделе 2.2) состояние игры — это состояние LG-системы. Как и в Теории Игр Гэйла-Стюарта, LG занимается поиском стратегии для обеих сторон (игроков), но вводит соответствующие определения на основе состояний LG-системы (или игры), а не на основе ДИ. В фокусе LG, тем не менее, оказываются эффективно вычисляемые стратегии. Это соответствует конструктивному подходу к обнаружению выигрышных стратегий в Теории Игр 2-х игроков Гэйла-Стюарта, впервые введенному Бухи и Ландвебером (1969) и продолженному Гуревичем и Харрингтоном (1982), А.Яхнисом и В.Яхнисом (1990, 1993), Мак-Нотоном (1993) и Зейтманом (1994). Близость целей последнего подхода к LG иногда проявляется в полном совпадении: речь идёт о тех случаях, когда в LG вычисляется доказуемо победная (ничейная) стратегия для игрока (глава 13). В других случаях, LG вычисляет стратегию, которая является хорошей, но может быть сложно или практически невозможно проверить, действительно ли эта стратегия является выигрышной для данного игрока. Алгоритмы Теории Игр, строящие выигрышные стратегии обычно практически неприменимы из-за экспоненциального (или ещё худшего) времени исполнения, в то время как LG-алгоритмы являются практическими и даже полиномиальными по времени (для подклассов задач). Немного перефразируя, данное в Теории Игр, определение стратегии для игрока на ДИ, мы получим определение LG-стратегии, основанной на состояниях игры. Стратегия — это частичная функция на состояниях игры, которая генерирует ходы для этого игрока. Выигрышная стратегия игрока — это такая стратегия, которая удовлетворяет двум свойствам. Во-первых, стратегия определена в каждом состоянии, в которое игрок должен попасть, следуя ей, а также в состояниях, которые уже были сгенерированы с использованием этой стратегии, включая начальное состояние. Во-вторых, любые конечные последовательности ходов обеих сторон, сгенерированные выигрышной стратегией, приведут систему из начального состояния в целевые состояния для данного игрока, в то время как противоположная сторона может делать любые ходы, разрешённые правилами игры. Дальнейшие подробности об LG-стратегиях приведены в главе 13. Мы определили стратегию, используя ДИ, включающее все возможные ходы обеих сторон. Однако LG-алгоритм не генерирует это ДИ. Процедура LG-перебора формирует очень маленькое поддерево полного ДИ путём генерации маленького подмножества всех состояний системы. В разделе 1.4 и далее в этой книге, это поддерево названо LG-деревом (или сокращённым деревом перебора) в противоположность полному ДИ при поиске решения методом "брут форс". Доказано, что для некоторых классов задач LG-дерево включает ветви, которые содержат последовательности ходов, сгенерированные выигрышной (или ничейной) стратегией (глава 13). Для других классов задач это сокращённое дерево включает ветви, соответствующие последовательностям ходов, которые сгенерированны с использованием лучшей стратегии, известной экспертам (в то время как никакая (абсолютно) выигрышная стратегия вообще неизвестна). Также, далее в этой книге, мы пишем "деревья ходов", "ветви (или последовательности) ходов" и "варианты" (виртуальные розыгрыши), опуская формулировки о взаимно однозначном соответствии между рёбрами деревьев и ходами игроков. LG-алгоритм вычисляет стратегию игрока, выбирая ветви, полученные при применении МиниМаксного алгоритма на LG-дереве для обоих игроков. Практически генерация LG-дерева и МиниМакс объединены в одной процедуре. В некоторых случаях LG-дерево является настолько маленьким, что во всех вариантах (игры) выигрывает один и тот же игрок. Другими словами, это LG-дерево представляет выигрышную стратегию (глава 13) для данного игрока. Возможно (хотя это и не гарантировано), что найденная LG-стратегия будет выигрышной также и для полного ДИ. LG-система функционирует, переходя из одного состояния в другое, т.е. ход игрока вызывает переход из текущего состояния LG-системы в другое состояние. Если последовательность состояний при переходах не имеет цикла, то эта последовательность определяет уникальный вариант (розыгрыш) на ДИ. Если последовательность состояний при переходах повторяется (циклит), то мы получим много розыгрышей, соответствующих одной последовательности переходов. Эти розыгрыши отличаются только тем, сколько раз они повторяют ходы, соответствующие одному периоду (циклу) последовательности состояний. Другими словами, розыгрыши отличаются лишь тем, по сколько раз они повторяют цикл. Важный факт состоит в том, что последовательности переходов в LG-системе образуют граф, а не дерево. Однако, важнейшие решения о том, закончена ли игра, и кто выиграл, основаны на состояниях LG-системы, а не на позициях ДИ. Это происходит из-за того, что в LG формулировки заключительных целей игроков основаны на описании целевых состояний LG-системы. Важно различать два случая использования LG-алгоритма, касающиеся развития LG-системы. Один случай, когда LG-стратегия одного игрока применена против LG-стратегии другого игрока. Другой случай, когда противник делает ходы не по LG-стратегии. Во всех случаях LG-стратегия представлена тем же самым LG-алгоритмом, в котором игрок, ход которого ищется, является входным параметром алгоритма. Другое важное различие имеется между ходами в игре и ходами в вариантах игры (или в виртуальных розыгрышах или, просто, в вариантах). Ходы в игре — это последовательность ходов, которые были фактически сделаны игроками в процессе игры. Ходы в вариантах — это последовательности ходов (обоих игроков), которые строятся LG-стратегией, чтобы вычислить очередной ход игрока. Такие последовательности ходов — это возможные продолжения уже начавшейся партии (розыгрыша) и они вовсе не должны состоять (полностью или в значительной степени) из ходов, уже фактически сделанных игроками. LG-стратегия должна заново построить LG-дерево в каждом состоянии, для которого вычисляется ход игрока. Если LG-стратегия вычисляет ход для игрока в состоянии S1, а следующий ход противника ведёт в состояние S2, то оба состояния будут содержать много общих структурных компонентов, потому что они отделены только двумя ходами: ход игрока и ответный ход противника, если мы рассматриваем последовательные игры. Для параллельных игр эти состояния разделены одним (параллельным) ходом. Таким образом, LG-алгоритм пытается построить LG-дерево для состояния S2, преобразовывая его из LG-дерева для состояния S1. Можно считать, что LG-стратегия вычисляет ход для игрока, находящегося в состоянии S системы, построением подмножества графа всех переходов из одного состояния LG-системы в другое. Фактически, LG-алгоритм существенным образом использует информацию о порядке ходов. Вышеупомянутый граф, представляет все варианты, построенные LG-алгоритмом, при выборе очередного хода для игрока. В действительности, LG-алгоритм генерирует перечисление подмножеств этого графа, тем самым, фиксируя порядок ходов во всех вариантах. Это перечисление порождает поддерево ДИ, которое простирается настолько, насколько продолжаются варианты, вычисленные LG-алгоритмом. Поддерево соответствует розыгрышам игры, начинающимся в состоянии S. Обычно, LG-дерево — это "очень узкое и глубокое" конечное поддерево полного ДИ, которое соответствует розыгрышам игры, начиная из состояния S. Существует взаимно однозначное соответствие между поддеревом ходов, охватывающим все LG-варианты, с одной стороны, и перечислением подмножеств графа переходов LG-системы, соответствующих ходам во всех LG-вариантах, с другой стороны. Программная система, реализующая LG, поддерживает уже разыгранный вариант игры и его возможные продолжения — поддерево игры, которое представляет все найденные LG-варианты для последнего состояния игры (текущей позиции). LG-алгоритм также поддерживает обширные структуры данных (разд.1.5), связанные с состояниями и предназначенные для сокращения множества вычисляемых вариантов. |
|
|
| 1.6 Три этапа развития LG |
|
Также как в физике 17-го столетия, в области ИИ и, в частности в LG, важнейшие обобщения и крупнейшие достижения всё ещё впереди. Однако, весьма возможно, что их первые признаки уже рядом с нами. В этом отношении, было бы полезно оглянуться назад, обратившись к истории развития LG. Эта история может быть разделена на три этапа. В конце 50-х годов в Москве Михаил Ботвинник, доктор электротехники и чемпион мира по шахматам, начал проводить научные исследования методологии лучших шахматистов. Десять лет спустя, эти исследования привели к революционным идеям в построении шахматных программ, которые моделируют игру гроссмейстеров. В начале 70-х, доктор Ботвинник организовал и возглавил исследования по проекту ПИОНЕР с автором этой книги, как ключевым разработчиком. Эти исследования проводились в Москве во Всесоюзном Научно-Исследовательском Институте Электроэнергетики (ВНИИЭ). Они финансировались ГКНТ СССР и Министерством Энергетики СССР. Цель исследования состояла в том, чтобы изучить и реализовать в виде компьютерных программ методологию лучших шахматистов, а так же экспертов в других областях, в решении переборных задач почти без перебора, и применить этот подход к широкому спектру сложных практических задач. Ряд эффективных алгоритмов был разработан в рамках проекта ПИОНЕР (Ботвинник, 1979, 1984). Были проведены многочисленные эксперименты для сравнения систем, основанных на начальной модели (ПИОНЕР) с системами, использующими другие подходы. Эксперименты показали, что многие из задач, которые были вовсе не разрешимы при других подходах, успешно решались прототипами будущих LG-систем. Кроме того, на тех задачах (где сравнение было возможно), новые системы работали значительно быстрее, чем системы при других подходах. Проект ПИОНЕР продолжался до конца 80-х годов. Период времени 1958-1988 годов, заполненный предварительными разработками и обширными экспериментами в рамках проекта ПИОНЕР, можно рассматривать как первый этап развития LG (разд.1.7). Многократные попытки формализовать и, по возможности, обобщить эвристики, обнаруженные в ходе проекта ПИОНЕР, столкнулись с огромными трудностями. Эти попытки, начавшиеся в середине 70-х годов, были вызваны настоятельными требованиями многих учёных, которые хотели, чтобы результаты этого проекта оказались применимы в других проблемных областях. Другая цель состояла в том, чтобы понять фундаментальную природу результатов, применить формальный подход и теоретически оценить качество, полноту и вычислительную сложность алгоритмов, разрабатываемых в ходе проекта ПИОНЕР. Трудности были связаны с необычной природой эвристик, присущих построенной модели. В частности, математические средства, которые следовало применить для формализации, должны были отразить иерархическую и динамическую структуру модели, существенную гибкость подсистем, должны были допускать глобальное и эффективное управление как отдельно взятой подсистемой, так и всей иерархией подсистем. Разработку Иерархии Формальных Языков, как основу математической модели эвристических алгоритмов проекта ПИОНЕР, выполненную автором этой книги, можно рассматривать как второй этап истории развития LG (разд.1.8). Первые результаты были получены в 1979 году, но разработка продолжалась вплоть до 1990 года в Москве во ВНИИЭ, а позже во Всесоюзном Научно-Исследовательском Геологоразведочном Нефтяном Институте (ВНИГНИ). Эти исследования финансировались в рамках проекта ПИОНЕР и из других источников. 1990-й год — это начало третьего этапа развития (разд.1.9), когда LG определилась как самостоятельная область исследований в ИИ. Этот этап начался в Мак-Гилльском Университете, в Монреале, Канада. С сентября 1991 года и до настоящего времени, он продолжается в Университете Колорадо в Денвере, США. В 90-х годах, предварительная математическая модель была унифицирована и обобщена (Штильман, 1992-1998). Поскольку формальная лингвистика и геометрия операционной области и подсистем, были использованы совместно, новая перспективная модель была названа Лингвистической Геометрией (LG) в 1991 году. Ретроспективно, мы будем использовать название LG при ссылках на предварительные исследования и результаты (этапы 1-й и 2-й). Цели исследований на 3-м этапе включали разработку прочного теоретического фундамента, оценку вычислительной сложности классов задач, допускающих LG-подход, оценку точности решений, получаемых при использовании LG-инструментов, расширение применимости LG к новым проблемным областям для разработки эффективных LG-приложений, а также создание программного прототипа универсального LG-testbed (испытательного стенда) — среды для разработки и отладки приложений LG в разнообразных проблемных областях. Что не ожидалось и не планировалось заранее, так это перестройка верхнего уровня LG — Языка Переводов — при использовании так называемого беспереборного подхода. Способность генерировать доказуемо оптимальные решения для классов Рети-подобных задач вообще без перебора ходов, т.е. без какого-либо перебора на дереве, демонстрирует удивительную мощь LG, которая родилась из экспертных эвристик. Проведенные исследования позволили идентифицировать новый класс задач низкой (полиномиальной) вычислительной сложности среди задач, которые считались в вычислительном отношении трудными (экспоненциальными или хуже). В течение третьего этапа финансирование было обеспечено из многих источников, включая Национальный Научно-Исследовательский Совет (NSERC) Канады и Мак-Гилльский Университет в Монреале, Офис Научных Исследований ВВС США (AFOSR), Университет Колорадо в Денвере, США, Министерство Энергетики США через Сандийскую Национальную Лабораторию в Альбукерке. Вероятно, несколько важных событий, имевших место в 1999 году, включая публикацию этой книги и значительный грант от Агентства Перспективных Исследований Министерства Обороны США, помогут в развитии теории и разработке программных приложений LG для решения задач из реальной жизни. Возможно, эти события знаменуют начало нового четвертого этапа в развитии LG. |
|
|
| 1.7 Этап 1: проект ПИОНЕР |
|
Первые десять лет исследований, начиная с 1958 года, закончились публикацией книги "Алгоритм игры в Шахматы" (Ботвинник, 1968, 1970). В то время как математическое описание алгоритма было ещё недостаточным для программирования (и, возможно, несколько сомнительным), основные принципы сокращения перебора заложили прочный фундамент для дальнейшего развития. Другая публикация "Блок-схема Алгоритма игры в Шахматы" (Ботвинник, 1972) уже может рассматриваться как официальное начало проекта ПИОНЕР. К сожалению, обе вышеупомянутые публикации не включали ничего кроме идей и набора блок-схем для низкоуровневых процедур алгоритма. Собственно алгоритм и программу шахматный игры ещё только предстояло разработать. Группа исследователей, занятых в этом проекте, имела два предмета научных исследований: выдающихся экспертов (подобно самому Ботвиннику) и компьютерные программы (после того как они были разработаны). Эти программы включали шахматную программу ПИОНЕР 1.x и множество программ ПИОНЕР 2.x — 4.x для планирования народного хозяйства СССР и составления графика ремонтов. Взаимосвязи между этими предметами исследований приводили к постоянному пересмотру наших взглядов и к многократной перестройке алгоритмов и программ. Много старых и новых идей были проверены в ходе проекта ПИОНЕР. Например, идея Траекторий, ограниченных горизонтом, и идея о декомпозиции Сложной Системы в динамическую иерархию подсистем доказали свою важность с самого начала. Этого не произошло с подсистемой второго уровня — Сетью Траекторий. Определенная первоначально, как ключевая область боя, а позже как Зона (в многочисленных версиях) и как Цепочка фигур, эта подсистема прошла множество существенных и менее значительных изменений. Эвристические алгоритмы для генерации подсистем первого и второго уровня — Траекторий и Зон — были представлены в (Штильман, 1975, 1977, 1979, 1984a). Подобные проблемы возникали и с подсистемами высокого уровня, и с алгоритмом глобального управления, позже формализованным как Грамматика Переводов. К концу 1976 года первая версия шахматной программы ПИОНЕР был закончена. Она была проверена на решении шахматных этюдов. Конечно, цель состояла не только в том, чтобы решить эти этюды. При решении нужно было получить дерево перебора, близкое к тому, которое строит шахматный мастер. Что касается точности, то получаемые решения никогда не рассматривались как оптимальные. Кроме того, для огромного большинства этюдов оптимальные решения до сих пор неизвестны. Доказательство оптимальности при использовании традиционных алгоритмов типа "брут форс" требует огромного перебора, который часто превышает возможности любых компьютеров (разд.1.2). То, что обычно называют решением — это вариант (или несколько вариантов), которые признаны экспертами. Более глубокое понимание оптимальности и его роли в LG пришло намного позже на 3-м этапе развития LG (разд.1.9 и глава 13). Первые два этюда, отобранные для тестирования программы ПИОНЕР — этюд Рети и этюд М.Ботвинника-С.Каминера, считаются простыми для шахматиста. Однако эта простота скрыта за миллионами ходов в дереве перебора, которые должны быть проанализированы при поиске решения по методу "брут форс". Конечно, шахматный эксперт способен избежать этого множества вычислений. Во время экспериментов с ПИОНЕРом оценивалось множество параметров, включая коэффициент ветвления (разд.1.2), а также некоторые другие параметры перебора (Ботвинник, 1979, 1984). Дерево перебора, построенное ПИОНЕРом в январе 1977 года при решении этюда Рети, содержало 54 хода (T=54). Следовательно, принимая во внимание, что глубина перебора, необходимого для решения этой задачи должна быть не меньше L=6, мы получили коэффициент ветвления B≈1,68 (1.2.2). Деревья перебора, построенные традиционными шахматными программами для этого этюда, включают приблизительно 106 ходов. В этюде Ботвинника и Каминера (Ботвинник, 1979, 1984), общее количество ходов, включённых в перебор, было равно 145, максимальная глубина L=12 и B≈1,35. Хотя оба этюда могут быть решены традиционными шахматными программами, эти результаты были очень интересны из-за существенного уменьшения коэффициента ветвления. Одна из этих задач, этюд Рети, продолжает служить моделью для далеко идущих обобщений в LG (главы 3, 4, 6, 13 и 14). Среди разнообразных сложных задач, решённых ПИОНЕРом, мы обсудим ещё две. Обе задачи до сих пор не могут быть решены традиционными шахматными программами. Алгоритмы перебора с альфа-бета отсечением (разд.1.2) не в состоянии обеспечить существенное уменьшение коэффициента ветвления. Поэтому время, требуемое для расчёта, оказывается немыслимым. Первая задача — этюд Г.Надареишвили (Надареишвили, 1976; Ботвинник, 1979, 1984). Он был решён ПИОНЕРом в августе 1977 года. Общее количество построенных узлов было T=200, в то время как глубина перебора, требуемого для нахождения решения L=25. Следовательно, B≈1,14. Неуменьшенный коэффициент ветвления для алгоритмов типа "брут форс" здесь можно оценить как B≈15. Решение этого этюда продемонстрировало мощь эвристической модели, на которой основан ПИОНЕР. Динамическая иерархия подсистем, Траекторий и Сетей, позволила нам найти очень глубокое решение почти без ветвления. Конечно, это было всего лишь решение, одобренное экспертами. Тогда никто не поднимал вопроса об оптимальности или хотя бы о точности этого решения. Теперь, 20 лет спустя, мы можем предположить, что это — математический оптимум. Разумно ожидать, что это будет доказано при использовании идей беспереборного подхода в LG (глава 13) в ближайшем будущем. Этюд Надареишвили также послужил образцом для множества обобщений, включенных в эту книгу (глава 5). Вторая сложная задача — это позиция в середине игры из легендарной партии М.Ботвинник и Х.Р.Капабланка, сыгранной в 1938 году на АВРО-турнире (Голландия)(Ботвинник, 1984a). Эту шахматную комбинацию обычно рассматривают как бессмертный пример выдающегося шахматного мастерства. Начальная позиция содержит 19 фигур, а неуменьшенный коэффициент ветвления можно оценить как B≈20. Глубина перебора для этой задачи не должна быть меньше, чем 23. В апреле 1980 года программа ПИОНЕР построила дерево перебора из 40 узлов с коэффициентом ветвления B≈1,05 (Ботвинник, 1980a, 1980b, 1982, 1987). Решение, найденное ПИОНЕРом, было точно таким же, как и вариант в той партии 1938 года. Вероятно, это решение является доказуемо оптимальным. В 1981-1988 годах, все исследования и программные разработки по проекту ПИОНЕР проводились при помощи системы поддержки разработки программ, называвшейся РАБОЧИМ МЕСТОМ ПРОГРАММИСТА (PROGRAMMER'S WORKBENCH — PW), (Штильман, 1994f). Система PW была разработана Мирным, Ройзнером, Чудаковым и Штильманом (1986), и позже переработана и расширена Мирным, Чудаковым и Штильманом (1988). PW была предназначена для того, чтобы поддержать параллельную разработку и конфигурацию программного обеспечения (ПО) для крупномасштабных научно-исследовательских работ. ПИОНЕР и другие сложные проекты включали расширенный период опытной эксплуатации образцов (прототипов) ПО. В основном, компьютерные программы использовались как инструменты для научных исследований и перестройки сложных алгоритмов. Полный цикл жизни компьютерных программ рассматривался как последовательность прототипов. Каждый прототип должен был быть чрезвычайно гибким, чтобы обеспечить многократное перепроектирование. PW поддерживала многократные итерации при перестройке изменяющихся прототипов благодаря жесткому универсальному каркасу версий ПО. Дополнительно, PW эффективно автоматически поддерживала взаимодействие разработчиков в проекте ПИОНЕР, обеспечивая независимость проектировщиков PW от остальных сотрудников (пользователей PW) и одновременно поддерживая строгую дисциплину коллективных разработок. Хотя язык Dijkstra (Дейкстра, 1976; Грис, 1983; Штильман, 1994f) был входным языком (транслятора), полностью реализованным в PW, фактическая разработка (включая отладку) проводилась с использованием проблемно-ориентированного языка очень высокого уровня. PW позволила нам создавать, расширять и поддерживать различные версии этого языка и для других проблемных областей. PW была реализована на IBM 370/144 — оригинальном американском компьютере, на котором в эти годы и велась разработка ПИОНЕРа. Позже, PW инструменты использовались в нескольких НИИ на советских ЭВМ для разработки и поддержки крупномасштабных проектов в области Искусственного Интеллекта. Инструменты PW были подготовлены к модернизации для поддержки объектно-ориентированного программирования. Проект ПИОНЕР закончился разработкой одной из самых интересных и мощных эвристических моделей, основанной на эвристических сетях. Применение разработанной модели к шахматной игре было полностью реализовано в виде программы ПИОНЕР 1.x (Ботвинник, 1979, 1982, 1984, 1987, 1989). Аналогичная эвристическая модель была также реализована для долгосрочного календарного планирования в виде набора программ ПИОНЕР 2.x, 3.x, 4.x. Они использовались для составления графика ремонтов электроагрегатов, для сглаживания графика потребления мощности и для планирования народного хозяйства в прежнем СССР (Штильман, 1985a, 1993a). Эти модели (Штильман, 1976c, 1977, 1979, 1994a; Ботвинник, 1968, 1972, 1975, 1979, 1989), (Резницкий и Штильман, 1983; Резницкий, Бордюгов и Штильман, 1983), (Ботвинник и др., 1983; Ботвинник, 1989), (Штильман, 1978, 1985b, 1985c, 1993d) были представлены в форме идей, правдоподобных рассуждений и работающих программ. Эксперименты с программами составления графика ремонтов ПИОНЕР 2.x продемонстрировали преимущества нового подхода. Программа ПИОНЕР 2.1 для составления месячного графика ремонтов электроагрегатов генерировала различные графики с коэффициентом ветвления, не превышающим 1,06, что составляло 50..100-кратное уменьшение этого коэффициента по сравнению с методом "брут форс" (Резницкий и Штильман, 1983; Штильман, 1985a). Эксперименты с программой ПИОНЕР 2.2 по составлению годового (на период в 365 дней) графика ремонтов электроагрегатов также продемонстрировали уменьшение коэффициента ветвления до величины близкой к 1. В отличие от ПИОНЕРа 2.1, эта программа была способна максимизировать число электроагрегатов, включённых в график ремонтов, регулируя продолжительность ремонта этих агрегатов. Особые качества были продемонстрированы программой ПИОНЕР 2.3, которая генерировала годовые графики ремонта агрегатов, регулируя значения резерва мощности. Небольшие вариации резерва мощности (в пределах диапазона 6%) позволяли этой программе включать в план ремонта все электростанции, которые подали заявки. Самые интересные результаты в составлении графика ремонтов были получены программой ПИОНЕР 2.4 для составления годового графика с распределением многочисленных ресурсов, включая различные типы ремонтного персонала. Такая постановка задачи приводила к существенному росту коэффициента ветвления; программа сумела уменьшить этот коэффициент до 1,005. Это позволило генерировать высококачественные годовые графики ремонтов для Единой Энергосистемы бывшего СССР. Применение LG к календарному планированию и дополнительная информация о программах составления графиков ремонта представлены в главе 7. Программы ПИОНЕР 3.1 и 3.2 позволяли сглаживать еженедельные графики потребления мощности, сдвигая выходные дни для различных потребителей. Они уменьшили максимумы потребления мощности на 3,5% при уменьшении числа потребителей со сдвинутыми выходными (Ботвинник и Мирный, 1983). Главным достижением модели ПИОНЕР в применении к не шахматным областям была разработка программ ПИОНЕР 4.1 и 4.2 для планирования народного хозяйства СССР на периоды в 15 и 25 лет соответственно. Эти программы балансировали продукцию государственной промышленности и бюджет, основываясь на агрегированной модели, включавшей 18 отраслей народного хозяйства (Резницкий, 1987; Ботвинник, 1989). Результаты, полученные в рамках проекта ПИОНЕР при решении сложных переборных задач для различных проблемных областей, показывают, что реализация динамических иерархий привела к построению в высшей степени целенаправленных алгоритмов, которые генерировали деревья перебора с показателем ветвления близким к 1. Что было общего в этих иерархиях? Какие формальные средства могли бы быть использованы, чтобы отразить эту общность и применить её в других проблемных областях? |
|
|
| 1.8 Этап 2: Математические Инструменты |
|
В 1979-1990 годах была разработана первая версия формальных инструментов для LG (рис.1.5). История получения этих результатов — поучительна. Было ясно, что математические инструменты должны быть дискретными, символическими и должны отражать динамическую иерархию подсистем. Более точно эти требования описаны ниже. Математические инструменты должны отражать постановку задачи как системы локальных агентов и их местоположений. Агенты разделяются на две стороны с противоположными интересами. Агенты могут перемещаться, изменяя свои местоположения — пункты. Некоторые из пунктов остаются свободными от агентов, но могут быть заняты ими позже. Ход делается в течение одного временного интервала. Все интервалы должны быть равны по времени. Также, агенты должны иметь чёткие правила, ограничивающие их движения. Функционирование системы можно представить как вариант, состоящий из последовательности ходов. Каждый вариант может сравниваться с другими возможными вариантами. Решение задачи — это вариант, выбранный среди всех по некоторому критерию оптимальности. Типичная трудность такого выбора связана с числом возможных вариантов и, следовательно, с продолжительностью требуемого перебора. Весьма часто, для задач из реальной жизни, время перебора возрастает так сильно, что они становятся практически неразрешимыми. Формализация постановки задачи в том виде, как она описана выше, не представляла трудности. Этот класс задач мог быть формально представлен с использованием многочисленных уже существующих методов, причём все они эквивалентны. Однако, важно, чтобы выбранное формальное представление постановки для класса задач соответствовало формальному представлению метода, который использовался при решении этих задач, т.е. LG-подходу. Это представление должно было стать основой и математической средой для формального представления динамической иерархии подсистем. Формальная постановка задачи (глава 2) была разработана, следуя известным теориям формального решения задач и планирования, разработанным в статьях (Маккарти и Хайеса, 1969; Файкса и Нильсона, 1971; Сакердоти, 1975; Маккарти, 1980; Нильсона, 1980 и в других), которые основаны на исчислении предикатов 1-го порядка. Основная идея этой формализации была заимствована из системы STRIPS, разработанной Файксом и Нильсоном (1971). |
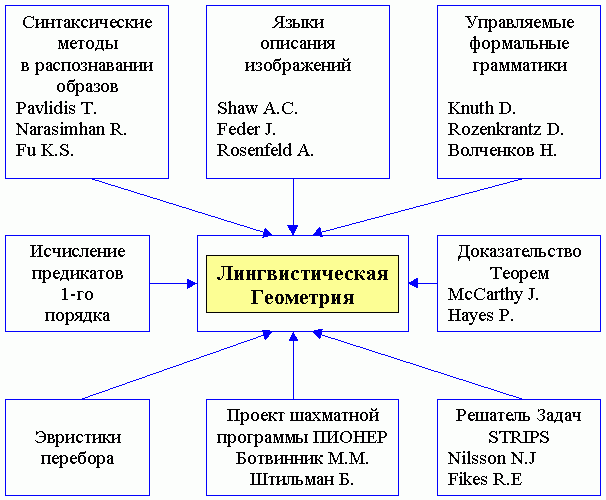
Рис.1.5 Происхождение LG: формальные инструменты и эвристики. |
|
Даже краткое описание требований для представления динамических иерархий, приведенное ниже, показывает, что проблема формализации этого представления была несравнимо труднее, чем формализация самой постановки задачи. Прошли годы, прежде чем удовлетворительное решение было получено. Иерархия, которую следовало ввести, должна была проявить и отразить ту глубокую иерархию взаимоотношений, которая возникает между агентами и группами агентов, при их стремлении к главной цели системы. Низший уровень иерархии — это Траектория, т.е. планируемый путь вместе с агентом, движущимся по этому пути. Когда агент продвигается, то пройденная часть траектории должна исчезнуть и вновь появиться при возврате агента в процессе перебора (когда агент "пятится"), чтобы исследовать другой путь. Формальные инструменты должны генерировать все виды траекторий для разных проблемных областей, например, самый короткий путь, путь для обхода препятствий и т.д. Более высокие уровни иерархии — это Сети Траекторий (вместе с их агентами). Каждая Сеть Траекторий должна иметь конечную цель с определенным местоположением, т.е. конечным пунктом назначения. Множество сетей должно включать Зоны нападения, Зоны доминирования, Зоны отступления и т.д. Каждая сеть должна включать агентов, участвующих в достижении конечной цели. Это участие является двойным. Агенты одной стороны преследуют свою цель, перемещаясь, защищая друг друга и уничтожая врагов. Агенты другой стороны подобными же действиями стараются препятствовать противнику в достижении его цели. Агент может участвовать во многих сетях одновременно. Движения агентов организованы с учётом времени. Например, если агент имеет достаточно времени, чтобы пройти по траектории и перехватить агента противоположной стороны, то эта траектория включается в сеть и движение по ней разрешается. Если дело обстоит не так, то траектория отбрасывается. При перемещении агентов в другие пункты часть траекторий и пучков траекторий сети застывает, когда движение агентов по ним уже не имеет смысла относительно конечной цели. Это может быть связано с недостатком времени, конфигурацией состояния (позицией) или с другими причинами. Вычисление времени и других параметров, связанных с построением и реконструкцией сети, производится для каждой сети независимо друг от друга. Связи с другими сетями при этом игнорируются. Сети могут быть связаны друг с другом, если конечная цель одной из них становится главной целью объединенной сети, тогда цели других сетей-компонентов подчиняются главной цели. В 70-х годах многие из известных математических инструментов были пересмотрены и отброшены. Обычно, они не отражали явно иерархию подсистем или не обеспечивали достаточную гибкость для представления их динамичности. Например, эти недостатки свойственны представлению траекторий и сетей в виде графов. В этой связи лингвистическое представление также рассматривалось в качестве кандидата. Действительно, траектория — это конечная последовательность запланированных ходов агента, в то время как слово — это конечная последовательность символов. Кажется, разумным представить траектории как формальные слова, составленные из символов. В этом случае множество траекторий можно представить как формальный язык. Но как с помощью языков представить иерархии? К нашему удивлению мы поняли, что лингвистическое представление иерархий является и наиболее естественным. Действительно, множество динамических подсистем можно представить как иерархию формальных языков, в которой каждое предложение — группа слов языка более низкого уровня — соответствует слову в высокоуровневом языке. Это стандартная процедура на нашем естественном языке. Например, фраза: "Человек, который преподаёт студентам", вводит иерархию языков. Символы языка низкого уровня могут включать все слова кроме слова "профессор". Высокоуровневый язык мог бы быть тем же самым языком, но дополненным ещё одним словом "профессор", которое является просто кратким обозначением для фразы "человек, который преподаёт студентам". Следует отметить, что иерархическая архитектура естественных языков и аналогичный подход, принятый в LG, — это примеры общего семиотического механизма мультирезолюций (иерархии моделей разного разрешения), введенного позже А.Майстелом (Майстел, 1996a, 1996b). Оставался ключевой вопрос о том, какие языки следует использовать для этой модели? В течение 50-70-х годов, формально-синтаксический подход к исследованию свойств естественного языка привёл к быстрому развитию теории формальных языков (Хомский, 1963; Гинсбург, 1966; Хопкрофт и Ульман, 1979 и другие). Это развитие предоставило интересную возможность для распространения лингвистического подхода в другие области. В частности, возникла идея об аналогичном лингвистическом представлении физических образов (рис.1.5). Эта идея была успешно разработана и воплощена в синтаксических методах распознавания образов (Нарасимхан, 1966; Фу, 1974, 1982; Павлидис, 1977) и языках описания изображений (Шоу, 1969; Федер, 1971; Розенфельд, 1979). Плекс-языки, введеные в (Федер, 1971), продемонстрировали значительную описательную мощь. В обычной строке символов каждый символ связан только с двумя соседями — левым и правым. Поэтому он имеет две точки сцепления. В Плекс-языке символ называется NAPE (n Attaching-Point Entity, т.е. n-связанный объект) и может иметь произвольное число n-точек сцепления для соединения с другими символами. Результирующие слова представляют общие многомерные образы, которые позволяют генерировать образы, представляющие деревья, сложные химические формулы, электрические схемы и т.д. Нечто аналогичное можно было бы сделать в LG с Траекториями и Сетями. В поисках адекватных математических инструментов, формализующих эвристику, мы преобразовали идею лингвистического представления сложных естественных и искусственных образов в идею аналогичного представления сложных иерархических систем (Штильман, 1981, 1984b, 1985a, 1985b, 1985c, 1992). Однако соответствующие языки должны были бы иметь более изощрённые и гибкие атрибуты, чем языки, обычно используемые для описания образов. Происхождение таких формальных языков можно проследить ретроспективно, начиная с исследований программируемых и атрибутных грамматик (Кнут, 1968; Розенкранц, 1969 и прочие). В этом отношении, особого внимания заслуживают результаты Н.Волченкова (1979) и Л.Кузина (1979). Волченков разработал исключительно мощные порождающие (генерирующие) грамматики, которые он называет БУППГ. Модификация и обобщение этих грамматик (Штильман, 1993a, 1993b) позволили нам построить языки, которые удовлетворяли всем требованиям для представления динамических иерархий. Эта модификация, названная управляемыми грамматиками (глава 8), позволила использовать их как универсальный инструмент на всех уровнях LG, формально доказывать правильность и полноту построенных языков, оценивать вычислительную сложность их порождения (главы 8-12 и 14). Новая версия управляемых грамматик рассмотрена в (В.Яхнис, А.Яхнис и Б.Штильман, 1996, 1997). До третьего этапа развития LG, в начале 90-х годов, формальные инструменты ещё не были организованы в полномасштабную математическую модель. Развитие программ ПИОНЕР на втором этапе было основано на наборе эвристических алгоритмов. Многократные эксперименты с этими программами позволили сделать далеко идущие обобщения и позднее построить математическую модель. |
|
|
| 1.9 Этап 3: Новейшая История |
|
С 1991 года этот подход называется Лингвистической Геометрией (LG) из-за геометрической природы обнаруженных эвристик и теории формальных языков, применённой для их формализации. Полная разработка двух уровней иерархии языков была представлена в (Штильман, 1993a, 1993b и 1994d). В 70-х и 80-х годах цели исследования были связаны с открытием наиболее глубоких особенностей экспертных эвристик перебора и разработкой математических инструментов, которые формализуют эти особенности. В 90-х годах с установлением LG как отдельной области цели изменились. На третьем этапе развития LG научные цели связаны с исследованием пределов эффективности, общности, вычислительной сложности и точности LG. Частичный список вопросов для исследований в области LG в 90-х годах приведен ниже. Какой должна быть наиболее эффективная общая структура программных реализаций LG? Существуют ли задачи высокой размерности, решаемые с использованием LG? Как повлияет на время расчётов переход от двумерных задач к трехмерным задачам? Как изменится время расчётов, если мы увеличим число агентов и обеспечим их более развитыми средствами перемещения? Сможем ли мы решать задачи с частично или даже полностью параллельными ходами, используя аналогичные формальные инструменты? Какова вычислительная сложность этих задач? К счастью, неожиданно для нас, в этот период мы получили ответы не только на эти, но и на другие дополнительные вопросы. Насколько точны решения LG? Можем ли мы строго оценить (и доказать) определённый уровень точности? Если наше доказательство конструктивно, можно ли использовать ту же самую технику для получения решения (а не только для оценки точности)? Все программы, разработанные в 70-х и 80-х годах в рамках проекта ПИОНЕР, были в высшей степени проблемно-ориентированными. Они служили реализацией эвристических иерархий подсистем для специфических проблемных областей. В 90-х годах мы начинали исследование различных подходов и программных инструментов для реализации общей иерархии формальных языков и их приложений. Несколько общих LG-грамматик были впервые реализованы в Университете Колорадо в Денвере в 1993 году Д.Кингом и Р.Матьюсом с использованием языка CLIPS и языка C, соответственно (Кинг, 1993) и (Матьюс, 1993). В то время как Р.Матьюс реализовал только два уровня иерархии — Траектории и Зоны (на C), Д.Кинг разработал прототип полномасштабной иерархии грамматик, используя среду программирования CLIPS. Он показал также, что инструменты программирования CLIPS (Гиарратано и Рилей, 1998), предназначенные первоначально для разработки экспертных систем, продемонстрировали высокую эффективность для быстрой реализации LG-грамматик. Конечно, эффективность на этапе разработки была достигнута за счёт снижения эффективности на этапе исполнения. Однако эти инструменты могут послужить основой для разработки прототипов. Другое направление исследований было связано с выяснением фактической актуальности применимости общих LG-инструментов к различным проблемным областям. В 1995 году C.Флечер реализовал Грамматики кратчайших и допустимых Траекторий с обобщенными отношениями достижимости, используя C++ (Флечер, 1996; Флечер и Штильман, 1997). Он применил этот инструмент для разработки программного прототипа для моделирования управления навигацией робота в индустриальной среде. Интерпретация различных движений робота через отношения достижимости позволила этой системе планировать близкие к оптимальным пути роботов и избегать столкновений с неподвижными и подвижными препятствиями. Различные версии этого прототипа демонстрировались в Сандийской Национальной Лаборатории, Научном Центре Рокуэлла и на множестве конференций. Проблемно-ориентированная версия LG-инструментов была разработана Р.Тюреком (Тюрек, 1996 и 1997). Он разработал очень эффективное коммерческое программное обеспечение, работающее в реальном времени, для прокладки маршрутов для машин экстренной помощи. Эти машины (полиция, пожарные и санитарные машины) направлялись к месту происшествия в ответ на телефонные звонки по номеру 911. LG-грамматики использовали отношения достижимости, которые формально представляли планы улиц и заторы движения на улицах города Авроры (часть Денвера), штат Колорадо. Планы улиц были введены при помощи географической информационной системы (GIS), в то время как информация о заторах обновлялась в реальном времени по данным от приборов, которыми комплектуются транспортные средства автодорожной полиции. Варианты этой программы демонстрировались в NASA в Центре Космических Полетов в Гринбелте, MD, и на нескольких конференциях. В 1996 году Д.Вуд разработал BGF — универсальную программную среду для настольных игр в виде апплетов на языке Java (Вуд, 1996). Этот инструмент был предназначен для разработки перспективных интерфейсов для приложений LG в различных проблемных областях. В 1997-98 годах Э.Скисов использовал BGF для дальнейшего совершенствования своего инструмента моделирования военных игр (Скисов, 1997). Этот инструмент моделирования военных игр (пока что наиболее полная реализация LG-алгоритмов) был разработан Э.Скисовым в 1997 году в рамках совместного проекта Университета Колорадо в Денвере и Университета Денвера (Скисов, 1997; Скисов и Б.Штильман, 1997, 1998a и 1998b). Его инструмент генерировал полномасштабную иерархию языков, включая предварительную версию Грамматики Переводов, основанную на беспереборном подходе (глава 13). Эта реализация была предназначена для исследования новых подходов в LG. В частности это был первый LG-инструмент, применённый к задачам с параллельным движением агентов. Также, это было первой реализацией LG для параллельной вычислительной среды на основе сети компьютеров. В этой среде вычисление траекторий с помощью Грамматики Траекторий происходило параллельно. Инструмент моделирования военных игр был реализован на C++ и на Java. Новая версия инструмента разрабатывается исключительно на языке Java. В 1998 году класс задач, в которых применима LG, был расширен путём включения задач для локальных агентов, перемещающихся с переменной скоростью. Это расширение приближает модели LG к задачам из реальной жизни. Михаил Штильман обобщил отношения достижимости и изменил Грамматику Кратчайших Траекторий для этого случая (М.Штильман, А.Яхнис и В.Яхнис, 1998), (ОПРЕДЕЛЕНИЕ 2.4 и разд.9.10). Его реализация этой грамматики (на C++) вычисляет все кратчайшие пути для самолёта, который должен избежать пролёта над некоторыми территориями. Вначале самолёт ускоряется, затем идёт по курсу с постоянной скоростью и в конце полёта он замедляется, чтобы приземлиться. В настоящее время исследуется применение LG к системам управления, где безопасность является критическим параметром. Это системы управления крылатыми ракетами, инопланетными исследовательскими аппаратами, системы национальной противоракетной обороны (с оценкой угрозы и контрмер), а также системы управления космическими военными операциями. По мере того, как общая структура и детали реализаций LG становятся более понятными, мы приближаемся к осуществлению нового проекта. Универсальный LG-testbad будет служить структурной средой для разработки приложений LG путём настройки на определенную проблемную область. Также, LG-testbad будет использоваться для быстрой проверки новых идей и подходов в LG. Чтобы ответить на вопросы о пределах применимости и требованиях к ресурсам для приложений LG, мы разработали набор задач постепенно возрастающей сложности. Некоторые из них были основаны на этюдах, которые рассматривались в прошлом: этюде Рети, этюде Надареишвили и других. Последовательность задач постепенно возрастающей сложности включала задачи с трёхмерной областью и областью с переменным размером n×n с большим числом агентов, со сложными параметрами подвижности, с чередующимся параллельным движением и полностью параллельным движением агентов и т.д. Решение этих задач с использованием LG-инструментов должно было обеспечить материал для дальнейших теоретических исследований. В 1993 году, реализованная на основе CLIPS, иерархия грамматик была применена к задаче оптимального управления четырьмя роботами в двумерном пространстве, участвующими в игре 2-х игроков. Задача была представлена как двумерная дискретная игра уклонения от преследования с 4 агентами — задача 2D/4A (Штильман, 1996a, 1997a и глава 3). В сущности, это была версия этюда Рети. Традиционные подходы требуют, чтобы дерево игры для решения этой задачи содержало миллион ходов. LG-инструменты позволили нам найти решение в виде LG-дерева, которое включало только 46 ходов с показателем ветвления 1,65. Интересный результат был получен в 1994 году, когда задача 2D/4A была обобщена для трёхмерного случая — задача 3D/4A (Штильман, 1994b, 1994c, 1996a и глава 4). Задача была представлена как игра уклонения от преследования космических станций, которые должны достигнуть определённых областей в пространстве, и космических кораблей, которые могут перехватить эти станции или предотвратить перехват. Традиционные подходы требуют, чтобы дерево игры для решения этой задачи содержало триллион ходов, в то время как дерево, сгенерированное LG-инструментами, содержало всего около 50 ходов с коэффициентом ветвления близким к 1. Очевидно, что LG-инструменты позволили нам устранить экспоненциальный рост времени исполнения (относительно входных данных) для этого класса задач (разд.4.4). Другой существенный тест для LG-инструментов в задачах со значительно большим пространством состояний проводился для двумерных и трёхмерных игр уклонения от преследования, в которых использовались 8 космических кораблей с необычайно сложными и развитыми возможностями перемещения (Штильман, 1995a, 1995b, 1997d и глава 5). Это была версия этюда Г.Надареишвили. Глубина решения и, соответственно, глубина перебора были чрезвычайно большими, по крайней мере, 25 ходов. Теоретические оценки показали, что для нахождения решения этих задач требуется генерация деревьев игры, которые бы включали приблизительно 1525 и 3025 ходов для задач 2D/8A и 3D/8A соответственно. Генерация дерева такого размера выходит за пределы разумных временных ограничений для любого компьютера. Однако, LG-деревья, сгенерированные LG-инструментами, состояли приблизительно из 150 ходов при коэффициенте ветвления 1,12. Эти примеры продемонстрировали существенный рост сложности задач от числа роботов, их способности к перемещению, размерности операционной области и, особенно, от требуемой глубины перебора. По тому, как увеличилась продолжительность анализа каждого состояния, можно предположить, что это был всего лишь полиномиальный рост (низкой степени) относительно длины входа. (Оценка времени исполнения представлена в главе 14). Деревья перебора практически не увеличились. Во всех экспериментах LG-деревья были очень маленькими, что позволяет нам предполагать, что размер этих деревьев также является полиномом низкой степени относительно входа. Можно заключить, что полное время вычислений, которое является произведением размера дерева перебора и времени анализа каждого узла (состояния), для моделей LG растёт как полином. В вышеупомянутых примерах подвижные объекты — самолёты, космические корабли и т.д. — перемещаются последовательно, т.е. один объект за один ход. Кроме того, движения объектов противоположных сторон чередуются. Нам было важно расширить применимость LG, охватив задачи с параллельным перемещением. На разных этапах развития LG формальное определение класса многоагентных систем, в которых применима LG, никогда не включало требования последовательных или чередующихся ходов, однако все примеры включали только последовательные перемещения. Новое направление, связанное с применением LG к многоагентным системам с высокой степенью параллелизма, определилось в 1994 году (Штильман, 1995c, 1995d, 1997a, 1997b и глава 6). Новый класс игр, называемый многоагентными играми на графе с одновременными ходами, был разработан В.Яхнисом и автором (1995). Эти новые игры разрешают одновременные (параллельные) ходы нескольких кооперирующих и конкурирующих агентов; кроме того, каждая сторона (суперагент) может пропустить ход или сделать ход путём одновременного перемещения одного или нескольких локальных агентов. Несколько примеров было разработано в 1994-95 годах. Мы постепенно увеличивали степень параллелизма, выясняя его воздействие на эффективность LG-инструментов (глава 6). Применение LG к задачам с полностью параллельными движениями первоначально финансировалось американскими ВВС в 1995 году в рамках летней программы для профессоров на базе Лаборатории Филипса, расположенной на Военно-Воздушной Базе Кэртланд (Штильман, 1997a). Прототип программы для генерации сценария воздушного боя в режиме реального времени был разработан в Лаборатории Филипса в 1995 году. Эта программа была предназначена для управления пилотируемыми и беспилотными самолётами, наводимыми датчиками, установленными на спутниках, для обнаружения и уничтожения подвижных вражеских пусковых установок ракет. В 1996 году эти исследования финансировались грантом от Сандийской Национальной Лаборатории. В этих задачах самолеты — свои и противника — могли летать одновременно. Разработанные задачи включали две противостоящих группы, по два самолёта в каждой группе. Введение параллелизма привело к существенному росту коэффициента ветвления, до 324 (если применять перебор по методу "брут форс"). Это число — основание степени при экспоненциальном законе роста размера дерева игры, которое должно быть построено. Однако, LG-дерево для этой полностью параллельной модели содержит только 40 ходов с коэффициентом ветвления примерно 1,5. Позже эти результаты были обобщены для n×n области (Штильман и Флечер, 1998; и главы 6, 13 и 14). В то время как введение параллелизма оказывает решающее влияние на время исполнения при использовании традиционных алгоритмов, этого, кажется, не происходит при использовании LG. Это означает, что LG-инструменты позволили выделить подкласс низких (полиномиальных) по сложности задач в классе задач, которые обычно рассматривались в вычислительном отношении как трудноразрешимые. Новый подкласс включает не только последовательные, но также и параллельные задачи (главы 13 и 14). Более глубокое исследование этих вопросов нам предстоит в будущем. Одно из последних достижений в LG — математическое доказательство оптимальности решений, полученных для некоторого класса задач, содержащего так называемые Рети-подобные задачи моделирования военных игр (Штильман, 1996b, 1997c, 1997d). Эти исследования финансировались грантом от Сандийской Национальной Лаборатории. Результат, полученный в 1996 году и позднее улучшенный, всё ещё выглядит удивительным для тех, кто вовлечён в исследования по LG. На протяжении всей истории развития LG значительные трудности виделись в том, как продемонстрировать качество приближённых решений, т.е. хороших или почти выигрышных стратегий, например, как измерить их точность. Как уже обсуждалось выше, это были решения одобренные экспертами. Существование ошибки даже не вызывало сомнений, потому что эвристические алгоритмы обычно не гарантируют оптимум. В течение многих лет мы пытались понять, как оценить степень этой ошибки. Удивительно, что эти исследования привели к доказательству отсутствия ошибки для Рети-подобных задач (разд.13.9). Этот новый результат свидетельствует о том, что LG-инструменты генерируют оптимальные решения для подкласса переборных задач. Оптимальность означает, что результат совпадает с решением, которое могло бы быть получено при использовании полного перебора по методу "брут форс". Самая интересная особенность этого доказательства состоит в том, что оно является конструктивным. Доказательство основано на декомпозиции Пространства Состояний (т.е. ДИ) на подпространства и построении множества путей между этими подпространствами. Каждый путь представляет потенциально выигрышную LG-стратегию для одного из суперагентов. Множество путей образует полное множество стратегий-кандидатов. Затем некоторые из стратегий-кандидатов отбрасываются как нереализуемые. Попытка реализации оставшихся стратегий-кандидатов, лучших для каждой из сторон, заканчивается фактическим построением решения — выбором (оптимальной) стратегии для этой задачи. Два решения, 1-е, построенное в процессе доказательства, и 2-е оригинальное, сгенерированное ранее LG-инструментами, совпадают. Однако, новое решение, полученное (в процессе доказательства) построением LG-стратегий, не использует вообще никакого перебора на дереве (т.к. не генерирует LG-дерева). Кроме того, оно доказуемо оптимально. В этой связи возникла мысль о конверсии доказательства в прямое построение LG-решений. Это было достигнуто в 1998 году (Штильман, 1998a, 1998b; и глава 13). Новый метод был назван беспереборным подходом. Беспереборной подход был расширен для охвата задач с параллельным движением агентов. Инструмент моделирования военных игр, разработанный Э.Скисовым, был впервые применён для экспериментов с параллельными задачами на основе беспереборного подхода (Скисов и Штильман, 1998a и 1998b). Задачи были решены с коэффициентом ветвления, равным точно 1, т.е. без ветвления в других направлениях. В настоящее время разработаны две версии верхнего уровня LG-алгоритма: Грамматика Переводов и Беспереборной Алгоритм. Первый является универсальным инструментом, применимым к различным задачам. Генерируя маленькое LG-дерево перебора, он не даёт формальных оснований для заключения о точности решения; обычно, он генерирует решения, которые являются лучшими среди известных. С другой стороны, Беспереборной Алгоритм генерирует доказуемо оптимальное решение — выигрышную стратегию без перебора на дереве, но в настоящее время он применим только к подклассу Рети-подобных задач. Обратите внимание, что термин "беспереборной подход" означает, что перебор на дереве устранён, но Алгоритм всё ещё может включать некоторые другие типы перебора, например, полиномиальные по времени переборы. Вероятно, будущие исследования, основанные на развитии беспереборного подхода, приведут к перестройке верхнего уровня иерархии языков — Языка Переводов. Помимо задач с подвижными объектами и противоположными сторонами (типа моделирования навигации робота), LG-инструменты могут быть эффективно применены к задачам без явного конфликта и противоположных сторон, например, к задаче составления расписаний с распределением ресурсов. Основы этого подхода были заложены применениями проекта ПИОНЕР к составлению графиков ремонтов и планированию на 1-м этапе развития LG (разд.1.7). Чтобы применить LG-инструменты, мы вводим искусственную игру двух игроков, т.е. искусственный конфликт, операционную область, подвижные объекты и противоборствующие стороны (Штильман и Флетчер, 1998, и глава 7). Эта формулировка позволила нам решить задачи высокой размерности, которые были неразрешимы при использовании традиционных подходов. |
|
|
|
ЭТЮДЫ |
|
|
|
Этюд Р.Рети, 1921.
Этюд М.Ботвинника и С.Каминера, 1925. Этюд Г.Надареишвили, 1950. М.М.Ботвинник — Х.Р.Капабланка, 1938. |
|
|
|
Этюд Р.Рети. Ничья. |
|
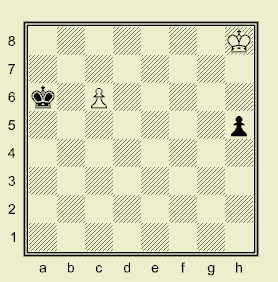
|
|
Этюд Р.Рети. Решение
|
Этюд Р.Рети. Решение 2
|
|
|
|
Этюд М.Ботвинника и С.Каминера. Белые начинают и выигрывают. |
|

|
|
Этюд М.Ботвинника и С.Каминера. Решение
|
|
|
|
Этюд Г.Надареишвили. Белые начинают и выигрывают. |
|
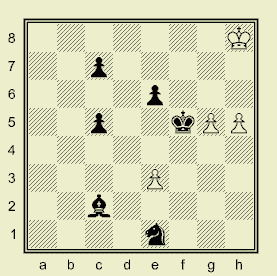
|
|
Этюд Г.Надареишвили. Решение
|
|
|
|
М.Ботвинник — Х.Р.Капабланка, 1938. Белые начинают и выигрывают. |
|
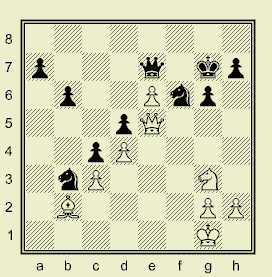
|
|
М.Ботвинник — Х.Р.Капабланка, 1938. Решение
|
|
|
Александр Тимофеев,
Это здесь —
г.Харьков, Украина, апрель—июнь 2005 года. eMail: atimopheyev@yahoo.com |
|
▲ В начало текущей ▲ Литература ▲ Этюды |
|
Последнее обновление 22.01.2011, size=806 894 bytes
© 2005 г., Александр Тимофеев, г.Харьков, Украина, резюме eMail: atimopheyev@yahoo.com |
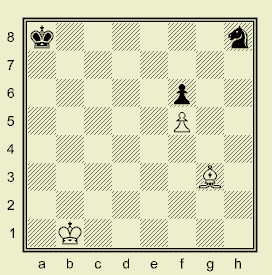

 Научился играть в шахматы в 12 лет и уже через два года имел первый разряд.
Победа над чемпионом мира Х.Р.Капабланкой в сеансе одновременной игры (1925, Ленинград)
принесла ему первую известность и придала уверенность в своих силах. В 16 лет самый
молодой мастер спорта в стране успешно дебютировал в чемпионате СССР, поделив 5-6-е места
среди 21 участника. В 1928-1932 учился в Политехническом институте. В начале 1930-х стал
одним из сильнейших шахматистов страны после побед на чемпионатах СССР (1931, 1933)
и Ленинграда (1931-1932). В 1933 сыграл вничью (3:3) матч с С.Флором, гроссмейстером
из Чехословакии, впоследствии жившим в СССР. В 1935 женился на Гаянэ Ананевой — балерине
Мариинского театра, ставшей верной спутницей жизни.
Научился играть в шахматы в 12 лет и уже через два года имел первый разряд.
Победа над чемпионом мира Х.Р.Капабланкой в сеансе одновременной игры (1925, Ленинград)
принесла ему первую известность и придала уверенность в своих силах. В 16 лет самый
молодой мастер спорта в стране успешно дебютировал в чемпионате СССР, поделив 5-6-е места
среди 21 участника. В 1928-1932 учился в Политехническом институте. В начале 1930-х стал
одним из сильнейших шахматистов страны после побед на чемпионатах СССР (1931, 1933)
и Ленинграда (1931-1932). В 1933 сыграл вничью (3:3) матч с С.Флором, гроссмейстером
из Чехословакии, впоследствии жившим в СССР. В 1935 женился на Гаянэ Ананевой — балерине
Мариинского театра, ставшей верной спутницей жизни.
 В 1935-36, после успешного выступления в трех крупных международных турнирах, заняв 1-е
и 2-е места в Москве (1935) и Ноттингеме (1936) и 2-е место в Москве (1936), стал одним из претендентов
на мировое первенство и достиг договоренности играть матч с А.Алехиным, который отмечал
у молодого соперника, помимо большого таланта, необходимые для успеха "бесстрашие, выдержку,
точное чутье". Из-за начавшейся войны матч не состоялся. Много времени уделял аналитической
работе над шахматами, разработал и опубликовал (1939) специальную методику подготовки к
соревнованиям, ставшую руководством для нескольких поколений отечественных шахматистов.
Стиль его игры претерпел эволюцию от комбинированного к универсальному. Внес ценный вклад
в развитие дебютной теории, введя в практику новые продолжения в английском начале,
славянской и голландской защитах и ряде других дебютов. Будущий чемпион мира по шахматам
во время войны работал в Перми инженером как специалист по высоковольтной изоляции.
В 1945 возглавлял сборную СССР в историческом радиоматче с командой США, в котором
советские шахматисты победили 15,5:4,5 (Ботвинник выиграл на первой доске у чемпиона США
А.Денкера со счетом 2:0). После внезапной смерти Алехина (1946) стал основным претендентом
на звание чемпиона мира. Выиграл крупные турниры в Гронингене (1946) и Москве (1947).
Победив в матче-турнире на первенство мира (1948), стал шестым в истории шахмат
чемпионом мира, опередив второго призера на три очка. В 1951-63 сыграл 7 матчей на
первенство мира — два вничью 12:12 (с Д.Бронштейном, 1951 и В.Смысловым, 1954),
В 1935-36, после успешного выступления в трех крупных международных турнирах, заняв 1-е
и 2-е места в Москве (1935) и Ноттингеме (1936) и 2-е место в Москве (1936), стал одним из претендентов
на мировое первенство и достиг договоренности играть матч с А.Алехиным, который отмечал
у молодого соперника, помимо большого таланта, необходимые для успеха "бесстрашие, выдержку,
точное чутье". Из-за начавшейся войны матч не состоялся. Много времени уделял аналитической
работе над шахматами, разработал и опубликовал (1939) специальную методику подготовки к
соревнованиям, ставшую руководством для нескольких поколений отечественных шахматистов.
Стиль его игры претерпел эволюцию от комбинированного к универсальному. Внес ценный вклад
в развитие дебютной теории, введя в практику новые продолжения в английском начале,
славянской и голландской защитах и ряде других дебютов. Будущий чемпион мира по шахматам
во время войны работал в Перми инженером как специалист по высоковольтной изоляции.
В 1945 возглавлял сборную СССР в историческом радиоматче с командой США, в котором
советские шахматисты победили 15,5:4,5 (Ботвинник выиграл на первой доске у чемпиона США
А.Денкера со счетом 2:0). После внезапной смерти Алехина (1946) стал основным претендентом
на звание чемпиона мира. Выиграл крупные турниры в Гронингене (1946) и Москве (1947).
Победив в матче-турнире на первенство мира (1948), стал шестым в истории шахмат
чемпионом мира, опередив второго призера на три очка. В 1951-63 сыграл 7 матчей на
первенство мира — два вничью 12:12 (с Д.Бронштейном, 1951 и В.Смысловым, 1954),
 три проиграл (В.Смыслову, 1957 — 9,5:12,5; М. Талю, 1960— 8,5:12,5
и Т. Петросяну, 1963— 9,5:12,5) и выиграл два матча-реванша (у В.Смыслова, 1958 —
12,5:10,5 и у М.Таля, 1961 — 13:8), стал единственным шахматистом, дважды возвратившим
звание чемпиона. Его слова "один матч на первенство мира отнимает два года жизни"
нередко повторяли последующие чемпионы.
три проиграл (В.Смыслову, 1957 — 9,5:12,5; М. Талю, 1960— 8,5:12,5
и Т. Петросяну, 1963— 9,5:12,5) и выиграл два матча-реванша (у В.Смыслова, 1958 —
12,5:10,5 и у М.Таля, 1961 — 13:8), стал единственным шахматистом, дважды возвратившим
звание чемпиона. Его слова "один матч на первенство мира отнимает два года жизни"
нередко повторяли последующие чемпионы.
 Успешно совмещал шахматную деятельность с научной работой в области электроэнергетики, став
автором ряда изобретений, запатентованных в различных странах мира. В 1951 защитил
докторскую диссертацию на тему: "Регулирование возбуждения и статическая устойчивость
синхронной машины". С начала 1970-х годов работал над созданием
Успешно совмещал шахматную деятельность с научной работой в области электроэнергетики, став
автором ряда изобретений, запатентованных в различных странах мира. В 1951 защитил
докторскую диссертацию на тему: "Регулирование возбуждения и статическая устойчивость
синхронной машины". С начала 1970-х годов работал над созданием






 другая. Теперь вопрос — какая задача решается сегодня искусственным интеллектом? Слушаю
внимательно и ничего не слышу... Поэтому я и ушел.
другая. Теперь вопрос — какая задача решается сегодня искусственным интеллектом? Слушаю
внимательно и ничего не слышу... Поэтому я и ушел.
 месяцев, там сегодня вообще не рассматриваются. Мы открыли новую линию — корпоративные
решения на карманных компьютерах. И американские инвесторы поставили нашим американским
партнерам условием срок окупаемости проекта не 36 месяцев, как это было раньше, а 12.
месяцев, там сегодня вообще не рассматриваются. Мы открыли новую линию — корпоративные
решения на карманных компьютерах. И американские инвесторы поставили нашим американским
партнерам условием срок окупаемости проекта не 36 месяцев, как это было раньше, а 12.
 умеешь, выполняешь ли ты задачи, которые удобны пользователю. Я, например, не боюсь поставить
свою подпись под таким заявлением. А много ли таких? Вот потому и не удалось.
умеешь, выполняешь ли ты задачи, которые удобны пользователю. Я, например, не боюсь поставить
свою подпись под таким заявлением. А много ли таких? Вот потому и не удалось.
 судебными исками, которые предъявляют Штаты "Микрософту". Они — как раз об этом, о том, что
нельзя одновременно с Linux поставить Microsoft Office по OEM-цене. Если корпорацию разделят,
думаю, что проблема может быть решена. Опять же, я Билла Гейтса ни в чем не виню. Если мне
дать ружье — я тоже постреляю. Нормально!
судебными исками, которые предъявляют Штаты "Микрософту". Они — как раз об этом, о том, что
нельзя одновременно с Linux поставить Microsoft Office по OEM-цене. Если корпорацию разделят,
думаю, что проблема может быть решена. Опять же, я Билла Гейтса ни в чем не виню. Если мне
дать ружье — я тоже постреляю. Нормально!
 кого выставить играть против нее. В итоге выбрали 15-летнего Широва, который тогда играл
на уровне гроссмейстера, но официально им не был. Ему просто нужно было набрать некоторое
количество баллов на турнирах. Стоит заметить, что машина играла всего лишь на уровне первого
разряда. Но ведь нужно было непременно доказать превосходство советского ума над американской
техникой. Во время подготовки программы визита я предложил подарить Кэну майку с символикой
московских Олимпийских игр 1980 года — он коллекционировал различные майки и был бы
наверняка рад небольшому сувениру. Шахматы хоть и не включены в программу Олимпийских игр,
но все же были далеко не последним видом спорта в СССР. После трехдневных дебатов комитет
вынес свой вердикт — олимпийских маек в спорткомитете не осталось.
кого выставить играть против нее. В итоге выбрали 15-летнего Широва, который тогда играл
на уровне гроссмейстера, но официально им не был. Ему просто нужно было набрать некоторое
количество баллов на турнирах. Стоит заметить, что машина играла всего лишь на уровне первого
разряда. Но ведь нужно было непременно доказать превосходство советского ума над американской
техникой. Во время подготовки программы визита я предложил подарить Кэну майку с символикой
московских Олимпийских игр 1980 года — он коллекционировал различные майки и был бы
наверняка рад небольшому сувениру. Шахматы хоть и не включены в программу Олимпийских игр,
но все же были далеко не последним видом спорта в СССР. После трехдневных дебатов комитет
вынес свой вердикт — олимпийских маек в спорткомитете не осталось.


 широко освещавшиеся шахматные поединки человека и машины в
последние несколько лет приносили успех компьютерам. Последним
известным достижением компьютерных систем стал трехкруговой
матч-турнир трех известных гроссмейстеров против трех известных
шахматных программ осенью 2004 года. Играли Руслан Пономарев
(чемпион мира 2003 года; однако сегодня по рейтингу ЭЛО он лишь
15-й), чемпион мира среди юношей 12-14 лет Сергей Карякин и болгарин
Веселин Топалов, третий в мировом шахматном рейтинге. Компьютеры
представляли действующий чемпион мира, израильская программа Deep
Junior 9.0, программа Fritz, а также Hydra.
Компьютеры выиграли с перевесом в три очка.
широко освещавшиеся шахматные поединки человека и машины в
последние несколько лет приносили успех компьютерам. Последним
известным достижением компьютерных систем стал трехкруговой
матч-турнир трех известных гроссмейстеров против трех известных
шахматных программ осенью 2004 года. Играли Руслан Пономарев
(чемпион мира 2003 года; однако сегодня по рейтингу ЭЛО он лишь
15-й), чемпион мира среди юношей 12-14 лет Сергей Карякин и болгарин
Веселин Топалов, третий в мировом шахматном рейтинге. Компьютеры
представляли действующий чемпион мира, израильская программа Deep
Junior 9.0, программа Fritz, а также Hydra.
Компьютеры выиграли с перевесом в три очка.
 “
“











 Ботвинник именно в этом направлении и стал работать. Научный подход
у него постепенно утвердился на первом плане. По-моему, он не занимался
дома такими вопросами, как, скажем, новый ход или новая идея где-нибудь
на 15-м ходу, в каком-то варианте. Он разрабатывал целую систему. Это было
его счастье. Шахматы во многом были еще целиной, и он шел по ней "первым
плугом". А сегодня нам приходится довольствоваться новинками на 12-м, 15-м
ходу. Не всегда и до этого дойдешь! Ботвинник мог себе позволить делать
большие перерывы, не играть подолгу, скажем, отойти от шахмат на год и
заняться научной работой...
Ботвинник именно в этом направлении и стал работать. Научный подход
у него постепенно утвердился на первом плане. По-моему, он не занимался
дома такими вопросами, как, скажем, новый ход или новая идея где-нибудь
на 15-м ходу, в каком-то варианте. Он разрабатывал целую систему. Это было
его счастье. Шахматы во многом были еще целиной, и он шел по ней "первым
плугом". А сегодня нам приходится довольствоваться новинками на 12-м, 15-м
ходу. Не всегда и до этого дойдешь! Ботвинник мог себе позволить делать
большие перерывы, не играть подолгу, скажем, отойти от шахмат на год и
заняться научной работой...
 “
“













