|
|
|
|
|
|
|
|
|
Штильман Борис,
Лингвистическая Геометрия: от Перебора к Построению, 1999, 395 стр.
LG - математическая дисциплина, которая занимается поиском лучших стратегий в переборных задачах, относящихся к классу игр на абстрактной доске. LG выросла из проекта шахматной программы ПИОНЕР М.Ботвинника, в котором Борис Штильман был ключевым математиком и программистом. Удивительно то, что сейчас приложения LG - это управление навигацией роботов и беспилотных транспортных средств, моделирование боевых операций, составление расписаний, а не только шахматы или другие настольные игры. В отличие от традиционных подходов к поиску стратегий на дереве перебора, LG позволяет за разумное время вычислять лучшие и даже теоретически оптимальные стратегии в реальных боевых задачах.
Copyright © 1999 Борис Штильман. Все права охраняются законом.
Никакая часть этой публикации не может быть воспроизведена, сохранена в базе данных, дистрибьютирована или передана в любой форме или любыми другими средствами - электронными, механическими, фотокопированием, записью или иначе - без предшествующего письменного разрешения Бориса Штильмана.
|
|
|
|
|
|
|
ПРЕДИСЛОВИЕ
к переводу LG01.pdf на русский язык
Прошло ровно 4 года с тех пор, как рукопись книги "Лингвистическая Геометрия: от Перебора к Построению" была сдана в печать. По случайному совпадению, ровно столько же времени прошло с тех пор, как была основана компания STILMAN Advanced Strategies (далее STILMAN). В книге я писал о возможном начале четвёртого этапа развития LG - и он действительно начался в 1999 году в связи с открытием этой компании. В сущности, STILMAN - это пока ещё небольшое, но весьма эффективное научно-производственное объединение ("НПО" в советской терминологии), которое лидирует в разработке теории и приложений LG на четвёртом этапе.
Четыре года назад я не мог и предположить, сколь могучей окажется роль LG в военном деле, сколь многообразными и революционными окажутся её применения. Ещё поразительнее то, что эта проблемная область оказалась настолько глубокой и насыщенной, что уже оказала и продолжает оказывать плодотворное влияние на развитие общей теории LG.
Шахматы, как известно, родились около полутора тысяч лет назад путём абстрагирования реальных военных действий. Наверное, пришла пора платить по счетам - передать военным выигрышные стратегии, разработанные за много веков поколениями выдающихся шахматистов.
|
|
Борис Штильман
Денвер, США
октябрь, 2003
|
|
|
|
|
|
|
TABLE OF CONTENTS
Titul page
PREFACE
ACKNOWLEDGMENTS
1. Introduction......................................................1
1.1 Problems.........................................................2
1.2 Current Approaches...............................................4
1.3 LG Approach at a Glance..........................................9
1.4 LG Approach: Deeper Account.....................................13
1.5 LG Strategies and Game Theory...................................19
1.6 LG: Three Stages of Development.................................22
1.7 Stage One: Project PIONEER......................................24
1.8 Stage Two: Mathematical Tools...................................28
1.9 Stage Three: Modern History.....................................32
2. Hierarchy of Formal Languages....................................39
2.1 Hierarchy Outline...............................................39
2.2 Class of Problems...............................................40
2.3 Various Problems as Complex Systems.............................45
2.4 Set of Paths: Language of Trajectories..........................50
2.5 Board and State Distances.......................................52
2.6 Networks of Paths: Languages of Networks........................54
2.7 Representation of Movement: Translations........................66
2.8 Search by Construction: Languages of Searches...................71
2.9 Historical Remarks..............................................75
3. Robot Combat for 2D District.....................................77
3.1 Problem Statement...............................................77
3.2 LG Search.......................................................79
3.3 Discussion......................................................88
3.4 Historical Remarks..............................................89
4. Expanding to 3D Space............................................91
4.1 3D/4A Robot Combat..............................................91
4.2 LG Search within Insufficient Horizon...........................94
4.3 LG Search within Horizon 5......................................98
4.4 From 2D to 3D: Running Time Change.............................105
4.5 Historical Remarks.............................................106
5. Deeper Search, More Agents......................................107
5.1 2D/8A Air Combat...............................................107
5.2 Deep Search for Air Combat.....................................112
5.3 3D/8A Space Combat.............................................128
5.4 A New Level of Sophistication: Preliminary Conclusions.........131
5.5 Historical Remarks.............................................134
6. Concurrency, n×n District.......................................137
6.1 Serial Mode Relaxation: Partial Concurrency....................137
6.2 LG Search for Problem with Partial Concurrency.................139
6.3 Second Problem with Partial Concurrency........................143
6.4 Second Problem: LG Search......................................145
6.5 Problem with Total Concurrency and n×n District................150
6.6 Problem with Total Concurrency: LG Search......................155
6.7 Impact of Concurrency..........................................160
6.8 Historical Remarks.............................................162
7. Scheduling: Artificial Conflict.................................165
7.1 Problem Statement..............................................165
7.2 Conversion into Two-Player Game................................168
7.3 Scheduling: Search and Solution................................172
7.4 Formal Representation..........................................174
7.5 Evaluation and Implementation..................................177
7.6 Applicability of LG............................................178
8. Generating Techniques...........................................181
8.1 Chomsky Grammars...............................................181
8.2 Controlled Grammars: Introduction..............................183
8.3 Tower of Hanoi: 3 Discs........................................184
8.4 Tower of Hanoi: n Discs........................................186
8.5 Controlled Grammars: Formal Definition.........................188
8.6 Historical Remarks.............................................191
9. Language of Trajectories........................................193
9.1 Shortest Trajectories: Generating Grammar......................193
9.2 Generation of Shortest 2D Trajectories.........................196
9.3 Generation of Shortest 3D Trajectories.........................200
9.4 Shortest Trajectories: Correctness and Completeness............204
9.5 Admissible Trajectories: Generating Grammar....................207
9.6 Avoiding Obstacles: Generation of Admissible Trajectories......210
9.7 Admissible Trajectories: Correctness and Completeness..........215
9.8 Trajectories for the Game of Chess.............................219
9.9 Trajectories for Scheduling....................................224
9.10 Trajectories for Agents with Variable Speed...................226
9.11 Language of Trajectories: Efficient Implementation............232
9.12 Historical Remarks............................................233
10. Language of Zones..............................................235
10.1 Grammar of Zones..............................................235
10.2 Generation of Zones...........................................238
10.3 Geometry of Zones.............................................250
10.4 Zones for the Game of Chess...................................253
10.5 Zones for Scheduling..........................................254
10.6 Historical Remarks............................................256
11. Translations...................................................259
11.1 Approaching a Solution of the Problem of Change...............259
11.2 Theorem about Translations....................................265
11.3 Search with Translations......................................278
11.4 Translations and Freeze.......................................284
11.5 Historical Remarks............................................286
12. Languages of Searches..........................................287
12.1 General Searches..............................................287
12.2 Reduced Searches..............................................290
12.3 Grammar of Translations.......................................294
12.4 Quality of Trajectories and Zones.............................297
12.5 Tree Inspection Procedure.....................................300
12.6 Historical Remarks............................................303
13. From Search to Construction....................................305
13.1 Problem Statement.............................................305
13.2 Algorithm Outline.............................................306
13.3 Preliminary Definitions.......................................307
13.4 Terminal Sets Expansion.......................................308
13.5 Structure of Expanded Terminal Sets...........................311
13.6 State Space Chart.............................................319
13.7 Outline of Potential Strategies...............................323
13.8 Construction of Strategy at the Start State...................330
13.9 Strategies for Reti-like problems.............................335
13.10 Discussion...................................................337
13.11 Historical Remarks...........................................339
14. Computational Complexity.......................................341
14.1 Running Time: Conventional Algorithms
for Reti-like problems.......................341
14.2 Running Time: Grammar of Shortest Trajectories................347
14.3 Running Time: Grammar of Zones................................350
14.4 Running Time: Unfolding Bundles of Trajectories
and Cloning Zones............................353
14.5 Computational Complexity: Reti-like Problems..................357
14.6 Historical Remarks............................................359
Future Challenges..................................................361
References.........................................................363
Index..............................................................377
Chess Endgames
|
|
|
ОГЛАВЛЕНИЕ
Титульная страница книги
ПРЕДИСЛОВИЕ к переводу LG01.pdf на русский язык
ПРЕДИСЛОВИЕ
БЛАГОДАРНОСТИ
1. Введение..........................................................1
1.1 Проблематика.....................................................2
1.2 Современные подходы..............................................4
1.3 LG с первого взгляда.............................................9
1.4 Углублённое рассмотрение LG-подхода.............................13
1.5 Стратегии LG и Теория Игр.......................................19
1.6 Три этапа развития LG...........................................22
1.7 Этап 1: Проект ПИОНЕР...........................................24
1.8 Этап 2: Математические Инструменты..............................28
1.9 Этап 3: Новейшая История........................................32
2. Иерархии Формальных Языков.......................................39
2.1 Обзор Иерархии..................................................39
2.2 Классы Задач....................................................40
2.3 Различные Задачи как Сложные Системы............................45
2.4 Множество Путей: Язык Траекторий................................50
2.5 Расстояния на Доске и в Пространстве Состояний..................52
2.6 Сети Путей: Языки Сетей.........................................54
2.7 Представление Движения: Переводы................................66
2.8 Перебор через Построение: Языки Переборов.......................71
2.9 Исторические Замечания..........................................75
3. Бой Роботов в двумерной Области..................................77
3.1 Постановка Задачи...............................................77
3.2 LG-перебор......................................................79
3.3 Обсуждение......................................................88
3.4 Исторические Замечания..........................................89
4. Переход в трёхмерное Пространство................................91
4.1 3D/4A - Бой Роботов.............................................91
4.2 LG-перебор в пределах недостаточного Горизонта..................94
4.3 LG-перебор в пределах Горизонта 5...............................98
4.4 Переход от 2D к 3D: Изменение Времени Выполнения...............105
4.5 Исторические Замечания.........................................106
5. Более глубокий Перебор, больше Агентов..........................107
5.1 2D/8A - Воздушный бой..........................................107
5.2 Глубокий Перебор для Воздушного Боя............................112
5.3 3D/8A - Космический Бой........................................128
5.4 Новый Уровень Сложности: Предварительные Выводы................131
5.5 Исторические Замечания.........................................134
6. Параллелизм, n×n Область........................................137
6.1 Ослабление Последовательного Режима: Частичный Параллелизм.....137
6.2 LG-перебор для Задачи с Частичным Параллелизмом................139
6.3 Вторая Задача с Частичным Параллелизмом........................143
6.4 Вторая Задача: LG-перебор......................................145
6.5 Задача с Полным Параллелизмом и n×n Областью...................150
6.6 Задача с Полным Параллелизмом: LG-перебор......................155
6.7 Воздействие Параллелизма.......................................160
6.8 Исторические Замечания.........................................162
7. Составление Расписаний: Искусственный Конфликт..................165
7.1 Постановка Задачи..............................................165
7.2 Преобразование в Игру двух игроков.............................168
7.3 Составление Расписаний: Перебор и Решение......................172
7.4 Формальное Представление.......................................174
7.5 Оценка и Реализация............................................177
7.6 Применимость LG................................................178
8. Методы Генерации................................................181
8.1 Грамматики Хомского............................................181
8.2 Управляемые Грамматики: Введение...............................183
8.3 Ханойская Башня: 3 Диска.......................................184
8.4 Ханойская Башня: n Дисков......................................186
8.5 Управляемые Грамматики: Формальное Определение.................188
8.6 Исторические Замечания.........................................191
9. Язык Траекторий.................................................193
9.1 Кратчайшие Траектории: Порождающая Грамматика..................193
9.2 Генерация Кратчайших двумерных Траекторий......................196
9.3 Генерация Кратчайших трехмерных Траекторий.....................200
9.4 Кратчайшие Траектории: Корректность и Полнота..................204
9.5 Допустимые Траектории: Порождающая Грамматика..................207
9.6 Обход Препятствий: Генерация Допустимых Траекторий.............210
9.7 Допустимые Траектории: Корректность и Полнота..................215
9.8 Траектории для Игры в Шахматы..................................219
9.9 Траектории для Составления Расписаний..........................224
9.10 Траектории для Агентов с Переменной Скоростью.................226
9.11 Язык Траекторий: Эффективная Реализация.......................232
9.12 Исторические Замечания........................................233
10. Язык Зон.......................................................235
10.1 Грамматика Зон................................................235
10.2 Генерация Зон.................................................238
10.3 Геометрия Зон.................................................250
10.4 Зоны для Игры в Шахматы.......................................253
10.5 Зоны для Составления Расписаний...............................254
10.6 Исторические Замечания........................................256
11. Переводы.......................................................259
11.1 На пути к Решению Проблемы Отличий............................259
11.2 Теорема о Переводах...........................................265
11.3 Перебор с Переводами..........................................278
11.4 Переводы и Застывание.........................................284
11.5 Исторические Замечания........................................286
12. Языки Перебора.................................................287
12.1 Общий Перебор.................................................287
12.2 Сокращённый Перебор...........................................290
12.3 Грамматика Переводов..........................................294
12.4 Качество Траекторий и Зон.....................................297
12.5 Процедура Обхода Дерева.......................................300
12.6 Исторические Замечания........................................303
13. От Перебора к Построению.......................................305
13.1 Постановка Задачи.............................................305
13.2 Обзор Алгоритма...............................................306
13.3 Предварительные Определения...................................307
13.4 Расширение Терминальных Множеств..............................308
13.5 Структура Расширенных Терминальных Множеств...................311
13.6 Диаграмма Пространства Состояний..............................319
13.7 Обзор Потенциальных Стратегий.................................323
13.8 Построение Стратегий из Начального Состояния..................330
13.9 Стратегии для Рети-подобных задач.............................335
13.10 Обсуждение...................................................337
13.11 Исторические Замечания.......................................339
14. Вычислительная Сложность.......................................341
14.1 Время Выполнения: Традиционные Алгоритмы
для Рети-подобных задач......................341
14.2 Время Выполнения: Грамматика Кратчайших Траекторий............347
14.3 Время Выполнения: Грамматика Зон..............................350
14.4 Время Выполнения: Разворачивание Пучков Траекторий
и клонирование Зон...........................353
14.5 Вычислительная Сложность: Рети-подобные задачи................357
14.6 Исторические Замечания........................................359
Взгляд в будущее...................................................361
Литература.........................................................363
Индекс.............................................................377
Этюды
|
|
|
|
|
|
|
|
This book is neither about linguistics nor geometry. It is about search problems. Linguistic Geometry (LG) is an approach to construction of mathematical models for knowledge representation and reasoning about large-scale multiagent systems. A number of such systems (formally defined here as Complex Systems), including air/space combat, robotic manufacturing, software re-engineering, Internet cyberwar, etc. can be modeled as abstract board games (ABG). These are multi-player games whose moves can be represented by means of moving abstract pieces over locations on an abstract board. The dimensions of the board (2D, nD, and even non-linear space), its shape and size, the mobility of pieces, the turn of moves (including concurrent moves) - all can be tailored to model a variety of multiagent systems. Thus abstract board games are understood here as a class of Complex Systems. The purpose of LG is to provide strategies to guide the participants of a game to reach their goals. Traditionally, finding such strategies required searches for suitable branches in giant game trees. Such searches are often beyond capabilities of modern and even conceivable future computers.
|
|
Эта книга не о лингвистике и не о геометрии. Она - о переборных задачах. Лингвистическая Геометрия (LG) - это подход к построению математических моделей для представления знаний и логического вывода в крупномасштабных многоагентных системах. Множество таких систем (формально определяемых здесь как Сложные Системы), включая воздушный бой, роботизированное производство, конверсию программного обеспечения, кибервойну в Интернете и т.д., образуют все те системы, которые могут быть смоделированы как абстрактные настольные игры (ABG). Сложные Системы - это игры многих игроков, ходы которых могут быть представлены передвижениями абстрактных фигур по полям абстрактной доски. Размерность (пространства) абстрактной доски (2D, nD и даже его нелинейность), его форма и размер, подвижность фигур, очерёдность ходов (включая одновременные ходы) - всё это может быть использовано для моделирования разнообразных многоагентных систем. Таким образом, абстрактные настольные игры понимаются здесь как класс Сложных Систем. Цель LG состоит в том, чтобы обеспечить участников игры стратегиями, необходимыми для достижения их целей. Традиционно, чтобы найти такие стратегии нужно перебрать все ветви в гигантском дереве игры (ДИ). Такой перебор часто превышает (по ресурсам времени и памяти) возможности современных и даже мыслимых компьютеров будущего.
|
|
|
LG dramatically reduces the size of the search trees, thus making the problems computationally tractable. LG provides a formalization and abstraction of search heuristics of advanced experts. Essentially, these heuristics replace search by construction of strategies. The formalized expert strategies yield efficient algorithms for problem settings whose dimensions may be significantly greater than the ones for which the experts developed their strategies. Moreover, these formal strategies allowed to solve problems from different problem domains far beyond the areas envisioned by the experts. It is really fascinating that for certain classes of problems these expert strategies yield provably optimal solutions. To formalize the heuristics, LG employs the theory of formal languages (i.e., formal linguistics), as well as certain geometric structures over the abstract board. Since both, the linguistics and the geometry, were involved, this approach was named Linguistic Geometry.
|
|
|
LG позволяет значительно уменьшить объём перебора, делая переборные задачи решаемыми. LG обеспечивает формализацию и обобщение эвристик перебора, заимствованных у лучших экспертов. По существу, эти эвристики заменяют перебор построением стратегий. Формализованные экспертные стратегии вполне масштабируемы, т.е. они приводят к эффективным алгоритмам для приложений, размерности которых могут быть значительно больше тех, для которых эксперты разрабатывали свои стратегии. Кроме того, эти формальные стратегии позволили в различных областях решать новые задачи, с которыми эксперты ещё не сталкивались. Удивительно то, что для некоторых классов задач эти экспертные стратегии доказуемо приводят к оптимальным решениям. Чтобы формализовать эвристики, LG использует теорию формальных языков (т.е. формальную лингвистику), а также некоторые геометрические структуры на абстрактной доске. Поскольку обе дисциплины - лингвистика и геометрия - были использованы совместно, этот подход был назван Лингвистической Геометрией.
|
|
|
This is the first book on the subject. It is not my intention to present a complete theory of LG, because such a theory is yet to be completed. However, the book includes foundations of such theory.
|
|
|
Это первая книга по предмету. Я не намеревался представить здесь полную теорию LG, поскольку она ещё не закончена. Однако, эта книга включает основы теории LG.
|
|
|
LG already has a long and enlightening history. Chess, a Drosophila of Artificial Intelligence, contributed in a major way to the origin of LG. It continues to be an everlasting source of ideas and a driving force behind its development. Having started with computer experiments in 1972, continued with theoretical insights in the 80s, and formally established in 1991, LG has moved in many directions. Some of them are based on rigorous foundations, others - on sophisticated experiments. The purpose of this book is to introduce the reader to a multiplicity of approaches, ideas, and experiments. Every chapter is written as an essay on one topic in LG, theoretical or experimental, though all chapters are linked together and support each other.
|
|
|
LG имеет длинную и поучительную историю. Шахматы - дрозофила искусственного интеллекта (ИИ) - наибольшим образом способствовали созданию LG. Они и теперь остаются постоянным источником идей и движущей силой, подталкивающей развитие LG. Начавшись с компьютерных экспериментов в 1972 году, продолженных уже с развитием теоретических идей в 80-х и формально определившаяся в 1991, LG развивалась по многим направлениям. Некоторые из них основаны на строгих теоретических построениях, другие - на сложных и утонченных экспериментах. Цель этой книги состоит в том, чтобы представить читателю разнообразие подходов, идей и экспериментов. Каждая глава написана как эссе на одну тему в LG, теоретическую или экспериментальную, хотя все главы связаны вместе и поддерживают друг друга.
|
|
|
Chapter 1 includes introduction to the subject and a brief research background. Chapter 2 includes basic definitions and a survey of the LG formal tools, a hierarchy of formal languages. Chapters 3 through 7 cover a number of experiments with LG tools. They demonstrate how the LG algorithms solve problems of gradually increasing complexity. Besides interesting actual results, a detailed description of experiments is intended to develop an intuitive understanding of LG algorithms and their underlying structure. Armed with this intuition, a reader will be able to digest a formal description of LG tools in Chapters 8-12. Chapter 13 gives a new, much deeper account in the foundations of LG. By redeveloping the experiment from Chapter 3, it points a new direction in LG: solving search problems by construction of strategies (without any tree-based search). In Chapter 14 we discuss some issues of computational complexity. The book suggests that LG tools allow us to identify a wide subclass of tractable (polynomial) problems among those that are usually considered as intractable (exponential). The LG algorithms provide their solutions.
|
|
|
Глава 1 включает введение в предмет и краткую историю исследований. Глава 2 включает основные определения и обзор формализмов LG, т.е. иерархию формальных языков. Главы 3-7 охватывают несколько экспериментов с инструментами LG. Они демонстрируют, как алгоритмы LG решают задачи постепенно возрастающей сложности. Помимо интересных фактических результатов, детальное описание экспериментов предназначено развить интуитивное понимание алгоритмов LG и их общей структуры. Вооруженный этой интуицией, читатель будет способен воспринять формальное описание инструментов LG, приведенное в главах 8-12. В главе 13 основы LG рассмотрены более глубоко. Пересматривая эксперименты из главы 3, мы вводим новое направление в LG: решение переборных задач путём построения стратегий (без какого-либо перебора на дереве). В главе 14 мы обсуждаем некоторые вопросы вычислительной сложности. В этой книге высказывается предположение, что инструменты LG позволяют выделить широкий подкласс легко решаемых задач (т.е. полиномиально сложных) среди тех, которые обычно считались трудноразрешимыми (т.е. экспоненциально сложными). Алгоритмы LG обеспечивают эффективное решение задач из этого подкласса.
|
|
|
This book can be used as a textbook for a graduate or senior undergraduate course on LG for one or two semesters or a supplement to a course on AI. Some of this material was taught in the courses Knowledge Representation for Intelligent Systems and Complex Intelligent Systems at the University of Colorado at Denver. Also, many topics included in the book were presented as tutorials and short courses on LG around the world.
|
|
|
Книга может использоваться как учебник для дипломированного специалиста или старшекурсника по курсу LG в течение одного-двух семестров или в качестве приложения к курсу по ИИ. Часть этого материала преподавалась в курсе Представление Знаний для Интеллектуальных Систем и в курсе Сложных Интеллектуальных Систем в Университете Колорадо в Денвере. Также, многие из тем, включенных в эту книгу, ранее преподавались в качестве отдельных лекций и кратких курсов по LG, проводимых по всему миру.
|
|
|
I hope that the reader will share my excitement with the subject and join the army of researchers and practitioners that develop the theory and applications of LG. The book is not going to be an untouchable sacred source of information on LG for decades to come. My intention is to move the frontier, elicit interest, ignite research and development, to bring this book out of date, and write a new book that will further revolutionize our understanding of the subject.
|
|
|
Я надеюсь, что читатель разделит мою увлечённость предметом и присоединится к армии исследователей и практиков, которые развивают теорию и приложения LG. Книга не может полностью отразить постоянное развитие LG, она вовсе не предназначена для того, чтобы стать неоспоримым "священным" источником информации по LG в течение многих десятилетий. Моё намерение состоит в том, чтобы раздвинуть границы наших знаний, вызвать интерес, послужить толчком к дальнейшим исследованиям и, тем самым, побыстрее состарить эту книгу и написать новую, которая позволит ещё больше революционизировать наше понимание предмета.
|
|
Boris Stilman,
Denver, Colorado, USA
|
|
Борис Штильман,
Денвер, Колорадо, США,
|
|
|
|
|
|
|
|
It would have been impossible for me to write this book about Linguistic Geometry if it was not based on almost three decades of research. This research would have never advanced to the current level without major support of my adviser, colleagues and scientists from around the world, funding agencies, and computing centers.
|
|
Я не смог бы написать эту книгу о Лингвистической Геометрии, если бы этому не предшествовало почти три десятилетия исследований. Это работа никогда бы не достигла нынешних высот без поддержки моего научного руководителя, моих коллег и ученых со всего мира, агентств, финансирующих научные исследования, и вычислительных центров.
|
|
|
This book was inspired by the results of long and fruitful collaboration in the 70s and 80s with Professor Mikhail Botvinnik, my research adviser and project director. At the very beginning he shaped my thinking about complex search problems. One scientist said that this unimaginably difficult work could have started because Botvinnik, a chess player, did not anticipate the difficulties of programming, while Stilman, a computer scientist, did not anticipate difficulties of playing chess. Every time when the team of researchers experienced serious problems in the development of the project PIONEER, Dr. Botvinnik used to say: “If a human chess master can make it, a computer will make it as well”. He believed in the existence of a general algorithm, or a small collection of general algorithms, used intuitively by all the chess masters and grandmasters in playing chess. Essentially, discovery, simulation and generalization of these algorithms were the goals of the project PIONEER. An attempt to construct and investigate a mathematical model based on those algorithms is the goal of this book.
|
|
|
Эта книга была вдохновлена результатами долгого и плодотворного сотрудничества в 70-х и 80-х годах с профессором Михаилом Ботвинником, моим научным руководителем и лидером проекта ПИОНЕР. В самом начале работы он формировал мои взгляды на сложные переборные задачи. Один ученый как-то сказал, что эта невообразимо трудная работа, возможно, началась только потому, что Ботвинник-шахматист не представлял себе трудностей программирования, в то время как Штильман-математик и программист не представлял себе трудностей игры в шахматы. Каждый раз, когда у группы исследователей возникали серьёзные проблемы в работе над проектом ПИОНЕР, доктор Ботвинник имел обыкновение говорить: “Если человек, шахматный мастер, может это делать, то и компьютер тоже сможет это сделать”. Он верил в существование общего алгоритма или небольшого набора общих алгоритмов, интуитивно используемых всеми шахматными мастерами и гроссмейстерами при игре в шахматы. В сущности, разработка, моделирование и обобщение этих алгоритмов и было целью проекта ПИОНЕР. Попытка разработки и исследования математической модели, основанной на этих алгоритмах - цель этой книги.
|
|
|
Alexander Yudin, Alexander Reznitskiy, Mikhail Tsfasman, Mikhail Chudakov have worked with me in the 70s and 80s to develop project PIONEER. My friend and colleague, Vadim Mirniy, with whom we worked in the 80s provided major insights and pushed our research and software implementations to much higher level. Also, in the 70s an invaluable technical assistance in software development was provided by Dmitry Lozinskiy, Lidia Poltavets and Anatoliy Kostrukov.
|
|
|
Александр Юдин, Александр Резницкий, Михаил Цфасман, Михаил Чудаков работали со мной в 70-х и 80-х годах над проектом ПИОНЕР. Мой друг и коллега, Вадим Мирный, с которым мы работали в 80-х, проявил глубокую научную проницательность и продвинул наши исследования и программные реализации на значительно более высокий уровень. Также, в 70-х годах неоценимая помощь в разработке программного обеспечения была оказана Дмитрием Лозинским, Лидией Полтавец и Анатолием Кострюковым.
|
|
|
Four major scientists, the founders of computer science and engineering in the former Soviet Union, Academician Viktor Glushkov, Professors Bashir Rameev, Viacheslav Myasnikov and Nikolay Krinitskiy contributed to the establishment of the organizational framework, provided major funding and access to the state-of-the-art computers for project PIONEER.
|
|
|
Четверо знаменитых ученых, основателей информатики и разработки компьютеров в прежнем Советском Союзе, академик Виктор Глушков, профессора Башир Рамеев, Вячеслав Мясников и Николай Криницкий помогали организации работы, обеспечению финансирования и доступа к современным компьютерам в рамках проекта ПИОНЕР.
|
|
|
Project PIONEER and the first theoretical generalizations related to the origin of LG would have never succeeded without constant support of numerous Soviet scientists. I am grateful to all of them. Here, I would like to acknowledge those whose decisive support came at the most difficult times. They are Academician Nikolay Krasovsky, Academician-correspondent, Lenin Prize Winner Yakov Tsipkin, Academician-correspondents Yury Rudenko and Hermogen Pospelov, Professors Dmitry Pospelov, David Yudin, Vladimir Yakubovich, Georgiy Adelson-Velsky, Yuriy Shakarian, Gavriil Shalit, Lev Mamikoniants and Dr. Mikhail Donskoy.
|
|
|
Проект ПИОНЕР и первые теоретические обобщения, связанные с созданием LG, не увенчались бы успехом без постоянной поддержки многочисленных советских ученых. Я благодарен им всем. Я хотел бы выразить признательность тем, чья решительная поддержка приходила в самые трудные времена. Это академик Николай Красовский, член-корреспондент, лауреат Ленинской премии Яков Цыпкин, члены-корреспонденты Юрий Руденко и Гермоген Поспелов, профессора Дмитрий Поспелов, Давид Юдин, Владимир Якубович, Георгий Адельсон-Вельский, Юрий Шакарян, Гавриил Шалыт, Лев Мамиконянц и доктор Михаил Донской.
|
|
|
Scientific exchange with researchers from around the world allowed our team to overcome isolation of the former Soviet Union. A list of major participants of this exchange includes Professor Monty Newborn from McGill University, Canada, Professors Tony Marsland and Randy Goebel from the University of Alberta, Canada, Professor Jaap van den Herik from the University of Limburg, The Netherlands, Professor Ben Mittman from Northwestern University, USA, Dr. David Cahlander from CDC Corp., USA, Ken Thompson from Bell Labs, USA, Dr. Hans Meuer from the University of Mannheim, Germany, Dr. H.-J.Appelrath from the University of Dortmund, Germany, David Levy from London, UK.
|
|
|
Научный обмен с исследователями всего мира позволил нашей группе преодолевать изоляцию прежнего Советского Союза. Список основных участников этого сотрудничества включает профессора Монти Ньюборна (Monty Newborn) из Мак-Гилльского Университета, Канада; профессоров Тони Марсланда (Tony Marsland) и Рэнди Гобеля (Randy Goebel) из Университета Альберты, Канада; профессора Япа ван ден Херика (Jaap van den Herik) из Университета Лимбурга, Нидерланды; профессора Бена Миттмана (Ben Mittman) из Северо-западного Университета, США; доктора Дэвида Каландера (David Cahlander) из CDC Corp., США; Кена Томпсона (Ken Thompson) из Лабораторий Белла (Bell Labs), США; доктора Ханса Мойера (Hans Meuer) из Университета Мангейма, Германия; доктора Х.Дж.Аппелрата (H.J.Appelrath) из Университета Дортмунда, Германия; Дэвида Леви (David Levy) из Лондона, Великобритания.
|
|
|
I have a special debt to Professor Newborn who invited me to do research at McGill University in 1990. I am certain that without this invitation I would not have been able to continue research in LG.
|
|
|
Я особо признателен профессору Ньюборну, который пригласил меня для проведения исследований в Мак-Гилльском Университете в 1990 году. Уверен, что без этого приглашения я не смог бы продолжить исследования по LG.
|
|
|
In 1992, Professor Ervin Rodin from Washington University, St. Louis, MS, showed interest in further development and expansion of LG. As an editor-in-chief of the international journal Computers and Mathematics with Applications, he wrote: “... I would be very interested in publishing these types of works of yours (in LG - B.S.)” (Rodin, 1992). Some of the major results presented in this book were first published in this journal. Professor Rodin’s Center for Optimization and Semantic Control at Washington University contributed to the success of the First Symposium on LG and Semantic Control in 1995. In 1994, with respect to applying LG to combat simulation and control, he wrote: “I am familiar with Professor Stilman’s work on Linguistic Geometry and I believe that it may be a most worthwhile tool to attack the above-named subject (intelligent battlefield planning and control - B.S.)” (Rodin, 1994).
|
|
|
В 1992 году профессор Эрвин Родин (Ervin Rodin) из Вашингтонского Университета в Сент-Луисе, Миссури, проявил интерес к дальнейшему развитию и расширению исследований по LG. В качестве главного редактора международного журнала "Компьютеры и Математика с Приложениями" (Computers and Mathematics with Applications), он писал: “... Я был бы очень заинтересован в публикации Ваших работ на эту тему (по LG - Б.Ш.)” (Родин, 1992). Некоторые из основных результатов, представленных в этой книге были впервые опубликованы в этом журнале. Центр профессора Родина "Оптимизация и Семантическое Управление" в Вашингтонском Университете внес вклад в успех 1-го Симпозиума по LG и Семантическому Управлению в 1995 году. В 1994, в связи с применением LG к моделированию и управлению боем, он писал: “Я знаком с работами профессора Штильмана по Лингвистической Геометрии и полагаю, что LG - это может быть наиболее заслуживающий внимания инструмент для выше названного предмета (интеллектуальное планирование и управление боем - Б.Ш.)” (Родин, 1994).
|
|
|
In 1993, Dr. Raymond Lauzzana, an editor-in-chief of the international journal Languages of Design demonstrated interest in broadening the scope of the LG audience. He put a significant personal effort, guidance, and encouragement in my revising of the paper on LG for his journal to make it available for a multidisciplinary audience. He wrote: “... I would like to say that Dr. Stilman has an exciting and refreshing interdisciplinary attitude about his research. He has been able to expand his research in modeling two-player games into a general model for hierarchical systems. This greatly expanded the applicability of his work ... I personally appreciate the rigor with which he has approached the subject. I am sure that his work will have a substantial influence in the future” (Lauzzana, 1993).
|
|
|
В 1993 году доктор Раймонд Луззана (Raymond Lauzzana), главный редактор международного журнала "Языки Проектирования" (Languages of Design) заинтересовался расширением круга специалистов знакомых с возможностями LG. Он приложил значительные личные усилия, осуществлял руководство и поддержку при переработке мною статей по LG для публикации в его журнале, чтобы сделать LG доступной для самого широкого круга специалистов. Он писал: “... Я хотел бы сказать, что доктор Штильман продемонстрировал увлекательный, впечатляющий новизной подход к научным исследованиям. Ему удалось превратить свои исследования по моделированию игр двух игроков в разработку общей модели иерархических систем. Это значительно расширило применимость его работ по LG... Я лично высоко оцениваю строгость, с которой он подошёл к предмету. Я уверен, что его работа окажет существенное влияние в будущем” (Луззана, 1993).
|
|
|
Jim Rash, a scientist from NASA Goddard Space Flight Center, Greenbelt, MD, provided support, impetus and encouragement for further development of LG. As a guest editor of the special issue of the international journal Telematics and Informatics (with the best papers of the 1994 Goddard Conference on Space Applications of AI), he referred to my paper "Heuristic Networks for Space Exploration" (1994c), “...as an example of a particularly enticing application of AI ... This paper presents Linguistic Geometry as an efficient method for searching large solution spaces with respect to classes of problems that are known to be especially difficult, and applies the method to the problem of autonomous robot navigation planning” (Rash, 1994).
|
|
|
Джим Раш (Jim Rash), ученый из Центра Космических Полётов им. Годдарда (NASA), Гринбелт, MD, оказал поддержку, стимулировал и поощрял дальнейшее развитие LG. В качестве приглашённого редактора специального выпуска международного журнала "Телематика и Информатика" (Telematics and Informatics), включающего лучшие статьи Конференции по Космическим Приложениям ИИ 1994 года, он упомянул мою статью "Эвристические Сети для Исследования Космоса" (1994c), “... как пример особенно увлекательного приложения ИИ... Эта статья представляет Лингвистическую Геометрию как эффективный метод для поиска решений в больших пространствах состояний для классов задач, которые известны как особенно трудные, и применяет LG к задаче автономного планирования навигацией робота” (Раш, 1994).
|
|
|
I am grateful to Professor Alex Meystel from Drexel University, for his constructive interest in LG and continuous support. As an editor-in-chief of Wile Series in Intelligent Systems he not only encouraged me to complete this book at the very beginning of this work but already urged me to write another book on LG, maybe with different emphasis. Professor Meystel wrote: “... I would expect that multiple new results of LG will be incorporated by Knowledge Engineering in AI. Any further advancement in this area is unthinkable without taking advantage of the conceptual systems like Linguistic Geometry” (Meystel, 1998).
|
|
|
Я благодарен профессору Алексу Майстелу (Alex Meystel) из Дрексельского (Drexel) Университета, за его конструктивный интерес к LG и постоянную поддержку. Как главный редактор серии книг по Интеллектуальным Системам, публикуемых издательством Вайли (Wile Series in Intelligent Systems), он не только поощрял меня к быстрому завершению работы над этой книгой, когда я находился ещё в самом начале работы над ней, но даже убеждал написать новую книгу по LG, возможно, с другим акцентом. Профессор Майстел писал: “... Я ожидаю, что многочисленные новые результаты по LG будут включены в Инженерию Знаний ИИ. Любое дальнейшее продвижение в области ИИ невозможно себе представить без использования концептуальных систем подобных Лингвистической Геометрии” (Майстел, 1998).
|
|
|
A skeleton of the book was implicitly influenced by Professor Norman Foo from the University of New South Wales, Sidney, Australia , who wrote: “There cannot be any panaceas for search techniques as it is provable that the worst case is exponentially hard or worse. So, for any given idea, there will be classes of problems that will defeat it. However, it is entirely possible that large subclasses of problems that have good descriptions are susceptible to efficient attack. This is where Boris’ ideas in linguistic geometry come into their own. He has essentially found an interesting and useful subclass for which his ideas and representation promise efficient solutions. This is a significant contribution to the area” (Foo, 1996).
|
|
|
Схему этой книги мне неявно подсказал профессор Норман Фу (Norman Foo) из Университета Нового Южного Уэльса, Сидней, Австралия, который писал: “Не может быть никакой панацеи для методов перебора, поскольку доказано, что в худшем случае перебор экспоненциально сложен или даже ещё сложнее. Так, для любой идеи перебора найдутся такие классы задач, в которых она потерпит поражение. Однако вполне возможно, что существуют большие подклассы задач, которые могут быть хорошо описаны и окажутся поддающимися эффективной атаке. Это как раз то место, где идеи Бориса в области Лингвистической Геометрии представляют интерес. Он по существу нашел интересный и полезный подкласс, для которого его идеи и представления обещают эффективные решения. Это - значительный вклад в область ИИ” (Фу, 1996).
|
|
|
When the work on this book was almost completed, I learned about the following statements by Professor John McCarthy from Stanford University. In his comments about solving
R.Reti
chess endgame by computers he wrote: “Note that Reti’s idea can be implemented on a 100x100 board, and humans will still solve the problem, but present (conventional, i.e., brute force - B.S.) programs will not... Chess can serve as a Drosofila for AI if AI researchers try to make a program that (will) come up with the idea needed to solve the problem on a board of arbitrary size. Conversely, AI will not advance to human level if AI researchers remain satisfied with brute force as a substitute for intelligence... Would anyone seriously argue that it is impossible for a computer to solve the Reti problem by other than brute force?” (McCarthy, 1998). Of course, LG was developed independently and over a long period of time. However, it is fascinating that this research was driven by similar ideas.
|
|
|
Когда работа над этой книгой была почти закончена, я узнал о следующем заявлении профессора Джона Мак-Карти (John McCarthy) из Стэнфордского Университета. В своих комментариях о решении шахматного этюда
Рети
компьютерами он писал: “Обратите внимание, что идея Рети может быть реализована на доске размером 100x100 и люди всё ещё смогут решать эту задачу, но современные программы (традиционные, т.е. работающие по методу «брут форс» - Б.Ш.) уже не смогут... Шахматы по-прежнему будут служить дрозофилой для ИИ, если исследователи попробуют создать программу, которая сможет решать задачи на доске произвольного размера. Однако, ИИ не будет продвигаться к человеческому уровню, если исследователи ИИ удовлетворятся методом «брут форс» как заменой интеллекта... Будет ли кто-нибудь серьёзно утверждать, что компьютер не сможет решить этюд Рети методом, отличным от «брут форс»?” (Мак-Карти,1998). Конечно, LG была разработана независимо и за длительный период времени. Однако, удивительно, что исследования по LG вдохновлялись аналогичными идеями.
|
|
|
LG benefited greatly from the unique expertise of two scientists, my friends Dr. Vlad Yakhnis from Rockwell Science Center, CA and Dr. Alex Yakhnis from Pioneer Technologies, TX. They made significant contributions to the construction of winning strategies for two player games with perfect information. Their work influenced the definition of abstract board games employed by LG. I extend my special thanks to Dr. Vlad Yakhnis who contributed greatly to the re-development of the foundations of LG. I would like to express my sincere appreciation of Dr. Alex Yakhnis’ review of the draft of this book and his constructive comments.
|
|
|
LG значительно обогатилась при использовании уникальной экспертизы двух учёных, моих друзей доктора Владимира Яхниса (Vlad Yakhnis) из Научного Центра фирмы Рокуэлл (Rockwell Science Center), CA и доктора Александра Яхниса (Alex Yakhnis) из фирмы Пионерские Технологии (Pioneer Technologies), TX. Они внесли существенный вклад в построение выигрышных стратегий для игр двух игроков с полной информацией. Их работа повлияла на определение абстрактных настольных игр, используемых в LG. Я пользуюсь случаем, чтобы выразить особую благодарность доктору Владимиру Яхнису, который способствовал перестройке оснований LG. Я высоко оцениваю рецензию предварительного варианта этой книги, подготовленную доктором Александром Яхнисом, и, особенно, его конструктивные комментарии.
|
|
|
I thank my student David Knox for reading the draft of this book, for his invaluable comments, and for saying that this book is ... certainly readable.
|
|
|
Я благодарю моего студента Дэвида Нокса (David Knox), который прочитал черновик этой книги, за его ценные комментарии и за высказывание, что эта книга - ...всё же читабельна.
|
|
|
I use this opportunity to thank my friend Professor Tom Altman from the University of Colorado at Denver whose inspirational ideas and practical advice helped me significantly advance the theory and applications of LG. It is very important to have a friend you can rely on in the most difficult situations in research and beyond.
|
|
|
Я пользуюсь случаем поблагодарить моего друга профессора Тома Альтмана (Tom Altman) из Университета Колорадо в Денвере, вдохновляющие идеи и практические советы которого помогли мне значительно продвинуть теорию и приложения LG. Очень важно иметь друга, на которого Вы могли бы положиться в самых трудных ситуациях на работе и в жизни.
|
|
|
I am grateful to my son Michael, currently a freshman at Stanford, who contributed to the development of LG for the agents with variable speed and designed an amazing cover for this book.
|
|
|
Я благодарен моему сыну Мише, в настоящее время студенту 1-го курса Стэнфордского Университета, который внёс вклад в развитие LG для агентов с переменной скоростью и разработал удивительную обложку для этой книги.
|
|
|
Another person whom I would like to distinguish is Gary Folven, my publisher. His enthusiasm about this book and unimaginable patience helped me to successfully complete this work.
|
|
|
Ещё один человек, которого я хотел бы поблагодарить - это Гарри Фолвен (Gary Folven), мой издатель. Его энтузиазм в связи с изданием этой книги и невероятное терпение помогли мне успешно закончить эту работу.
|
|
|
In this brief survey it is impossible to acknowledge all the contributions. I would like to express my gratefulness to numerous researchers, practitioners, and students whose interest and efforts helped to clarify and advance various aspects of LG.
|
|
|
В этом кратком обзоре невозможно перечислить всех, кто внёс вклад в развитие LG. Я хотел бы выразить мою благодарность многочисленным исследователям, инженерам и студентам, интерес и усилия которых помогли прояснить и развить различные аспекты LG.
|
|
|
While in the USSR, this research was supported by the grants from the State Committee for Science and Technology (GKNT) and from the Department of Energy and Power Production (MinEnergo). An access to the most advanced computers was provided by the Computing Center of the State Planning Committee (GVC Gosplana), the Computing Center for Information on Science and Technology (VNTIC), and the Computing Center for Health Maintenance of the Government of Moscow (VCKP "Zdravoohranenie"). For many years a friendly, supportive environment of the National Research Institute for Electrical Engineering (VNIIE) assisted me in the development of LG.
|
|
|
В СССР эти исследования поддерживались грантами от Государственного Комитета по Науке и Технике (ГКНТ) и от Министерства Энергетики (МинЭнерго). Доступ к наиболее современным компьютерам был обеспечен Вычислительным Центром Госплана СССР (ГВЦ Госплана), Всесоюзным Научно-Техническим Информационным Центром (ВНТИЦ) и Вычислительным Центром Коллективного Пользования "Здравоохранение" при Правительстве Москвы (ВЦКП "Здравоохранение"). Много лет дружественная атмосфера интереса и поддержки Всесоюзного Научно-Исследовательского Института Электроэнергетики (ВНИИЭ) помогала мне в развитии LG.
|
|
|
While in Canada and in the USA, this research at various stages was supported by the National Sciences and Engineering Research Council (NSERC) of Canada and McGill University, by the U.S. Air Force Office of Scientific Research (AFOSR) via Summer Faculty Fellowship at the Air Force Phillips Laboratory, by the grant from the Department of Energy through Sandia National Laboratories, and by the University of Colorado at Denver Faculty Research Fellowship.
|
|
|
В Канаде и затем в США эти исследования на различных этапах поддерживались Национальным Научно-Исследовательским Советом Канады (NSERC) и Мак-Гилльским Университетом, Канада, Офисом Научных Исследований ВВС США (AFOSR), Летней Профессорской Стипендией Лаборатории Военно-Воздушных Сил им. Филипса (Air Force Phillips Laboratory), грантами от Министерства Энергетики через Сандийскую Национальную Лабораторию (Sandia National Laboratories), а также Исследовательскими Стипендиями Университета Колорадо в Денвере.
|
|
|
Currently, this research is supported by a substantial grant from the Defense Advanced Research Projects Agency (DARPA).
|
|
|
В настоящее время, эти исследования поддерживаются значительным грантом от Агентства Перспективных Исследований Министерства Обороны США (Defense Advanced Research Projects Agency - DARPA).
|
|
|
|
|
|
|
|
Linguistic Geometry includes the syntactic tools for knowledge representation and reasoning about multiagent systems by modeling them as abstract board games. The LG tools provide a basis for the evaluation of computational complexity and accuracy of solutions, and for generating computer programs for specific problem domains. LG allows us to discover the inner properties of human expert heuristics that are successful in a certain class of games. This approach provides us with an opportunity to transfer formal properties and constructions from one problem to another and to reuse tools in the new problem domain. In a sense, it is the application of the method of a chess expert to robot control or maintenance scheduling and vice versa.
|
|
Лингвистическая Геометрия (LG) включает синтаксические инструменты для представления знаний и логического вывода в многоагентных системах, путём моделирования их как абстрактные настольные игры. Инструменты LG позволяют оценить вычислительную сложность и точность решений, а также сгенерировать компьютерные программы для определенных проблемных областей. LG позволяет нам выявить внутренние, скрытые свойства эвристик человека-эксперта, которые продемонстрировали успех в некотором классе игр. Этот подход даёт возможность переносить формальные утверждения и конструкции от одной задачи к другой, т.е. повторно использовать инструменты в новой проблемной области. В некотором смысле, подход на основе LG - это применение метода шахматного эксперта к управлению навигацией робота или календарному планированию ремонтов и наоборот.
|
|
|
What do we know about the methods of a chess expert? Of course, a computer is the perfect tool for discovery and modeling of such methods. The history of computer chess began with a paper by Professor Claude Shannon (1950) in which he introduced the framework that guided further development. Employing mostly the brute force search, relying ultimately on computer speed, computer chess programs gradually increased their level of playing (Newborn, 1996). In the middle of the 90s, they reached the level of a grandmaster. After the May 1997 historical event, when the Deep Blue computer chess system defeated World Chess Champion Gary Kasparov, computer chess lost its exciting attractiveness. In June of 1997, Professor John McCarthy wrote: “In 1965 the Russian mathematician Alexander Kronrod said, «Chess is the Drosophila of Artificial Intelligence». However, computer chess has developed much as genetics might have if the geneticists had concentrated their efforts starting in 1910 on breeding racing Drosophila. We would have some science, but mainly we would have very fast fruit flies” (McCarthy, 1997).
|
|
|
Что мы знаем о методах шахматного эксперта? Конечно, компьютер - это совершенный инструмент для распознавания и моделирования таких методов. История компьютерных шахмат началась со статьи профессора Клода Шеннона (1950), в которой он предложил общую схему для последующих разработок. Используя, главным образом, поиск решения по методу полного перебора (англ. «брут форс» - грубая сила), т.е. полагаясь, в конечном счёте, на быстродействие компьютеров, шахматные программы постепенно улучшили свой уровень игры (Ньюборн, 1996). В середине 90-х годов, они достигли уровня гроссмейстера. После исторического события в мае 1997 года, когда Дип Блю (Deep Blue - компьютерная шахматная система фирмы IBM) победила чемпиона мира по шахматам Гарри Каспарова, компьютерные шахматы потеряли свою захватывающую привлекательность. В июне 1997 года, профессор Джон Мак-Карти писал: “В 1965 году российский математик Александр Кронрод сказал, что «шахматы - дрозофила ИИ». Однако компьютерные шахматы разрабатывались так, как могло бы случиться с генетикой, если бы усилия учёных концентрировались, начиная с 1910 года, только на выведении быстрой дрозофилы. Но тогда мы всё же имели бы немного науки, хотя главным образом, мы получили бы очень быстрых плодовых мушек” (Мак-Карти, 1997).
|
|
|
All the major advances in computer chess, including the Deep Blue triumph, were related to the brute force approach. What can we learn from these advances for different problems, particularly, for the problems of much higher dimension? Not much. Even in the future, we will not be able to solve these problems employing brute force. The grandmaster’s approach (of almost no search) has not been discovered yet. After the 1997 event, it is more important than ever before, that chess stays as a scientific Drosophila of AI and not just a racer (McCarthy, 1990, 1997).
|
|
|
Все самые большие успехи в компьютерных шахматах, включая триумф Дип Блю, были связаны с методом решения «брут форс». Сможем ли мы использовать какие-либо из этих результатов для решения других задач, особенно для задач, имеющих намного большую размерность? Вряд ли. Даже на суперкомпьютерах будущего, мы не сможем решать такие задачи по методу «брут форс». Метод гроссмейстера (т.е. почти без перебора ходов) пока ещё не раскрыт. После события 1997 года стало яснее, чем когда-либо прежде, что шахматы предназначены быть научной дрозофилой ИИ, а не только тестом для проверки скорости компьютеров (Мак-Карти, 1990, 1997).
|
|
|
Not all the research in computer chess went in the direction of the brute force. In the 70s and 80s project PIONEER led by the Former World Chess Champion, Professor Mikhail Botvinnik was developed in Moscow, Russia. In his book (1984) Botvinnik writes that the brute force method is “hardly capable of further progress. It is the computer’s turn to adopt a more fruitful method - perhaps PIONEER. And if PIONEER is unsuccessful, we must believe that other method will be found. The problem must and will be solved”.
|
|
|
Однако, не все исследования в компьютерных шахматах проводились в направлении поиска решений по методу «брут форс». В 70-х и 80-х годах в Москве (Россия) разрабатывался проект ПИОНЕР во главе с экс-чемпионом мира по шахматам профессором Михаилом Ботвинником. В своей книге (1984) Ботвинник писал, что метод решения «брут форс» “едва ли способен к дальнейшему прогрессу. Настала очередь принять компьютеру более плодотворный метод, возможно, ПИОНЕР. И, если ПИОНЕР неудачен, то мы должны быть уверены, что другой метод всё же будет найден. Задача должна быть и будет решена”.
|
|
|
LG is the direct successor of the project PIONEER. The Drosophila of AI “flies through this book fertilizing various experiments and generating new ideas”.
|
|
|
LG - прямой преемник проекта ПИОНЕР. Дрозофила ИИ “летит через эту книгу, оплодотворяя различные эксперименты и генерируя новые идеи”.
|
|
|
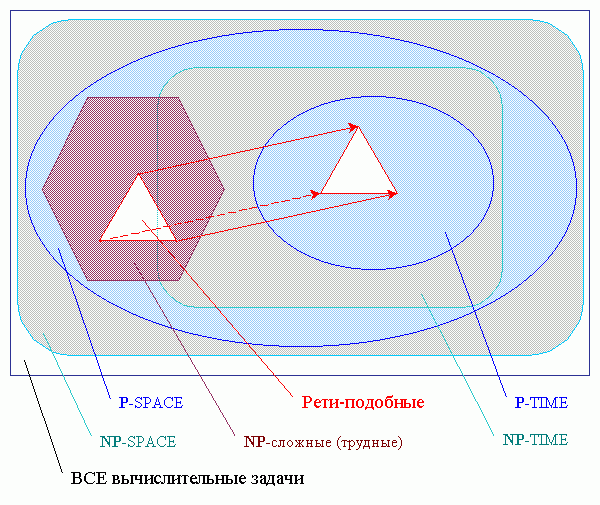
Among other examples in this book we consider a series of combat simulation problems. These are Reti-like problems, i.e., the generalizations of the
R.Reti
endgame (c.f. Botvinnik, 1984). Here they are called 2D/4A, 3D/4A, partially and totally concurrent combat simulations. These problems are simple enough to be used as demonstrations of the LG approach. On the other hand, they are not trivial and require significant search to be solved employing conventional approaches. It is the general understanding that they are
P-SPACE-complete or at least
NP-hard and no known polynomial-time algorithms exist to solve them (Garey and Johnson, 1991).
|
|
|
Среди других примеров в этой книге мы рассматриваем ряд задач моделирования боя. Это - Рети-подобные задачи, т.е. обобщения знаменитого этюда
Рети
(Ботвинник, 1979, 1984). Здесь они - называются задачами 2D/4A, 3D/4A, с частично и полностью параллельным моделированием боя. Эти задачи достаточно просты, чтобы использоваться для демонстрации LG-подхода. С другой стороны, они всё-таки не тривиальны и требуют существенного перебора, если их решать с использованием традиционных подходов. Важно общее понимание того, что Рети-подобные задачи являются
P-SPACE-полными или, по крайней мере, относятся к группе (или подклассу), так называемых,
NP-сложных задач, т.е. таких, для которых не существует алгоритмов, приводящих к решению за полиномиальное время (Гэри и Джонсон, 1991).
|
|
|
LG tools allow us to solve subclasses of these and many other problems employing algorithms of polynomial complexity. It can be suggested that the Reti-like problems are representative of a wider class of problems of low (polynomial) computational complexity. This would be a new subclass in the class of
P-TIME problems. It is likely that many important real world problems considered below are members of this subclass.
|
|
|
Инструменты LG позволяют нам решать задачи из этого подкласса и многие другие задачи, используя алгоритмы полиномиальной сложности. Поэтому можно предположить, что Рети-подобные задачи являются представителями более широкого класса задач с низкой (полиномиальной) вычислительной сложностью (т.е. их можно рассматривать и как новый подкласс в группе
P-TIME задач). Вероятно, многие важные задачи из реальной жизни, рассмотренные ниже, входят в этот подкласс (Рети-подобных задач).
|
|
|
|
|
Exist the classes of problems polynomial-time:
and polynomial-size:
here P — deterministic polynomial,
NP — nondeterministic polynomial.
The simplified classification of problems on computing
complexity.

|
|
Различают классы задач полиномиальной сложности по времени:
и по требуемой памяти:
где P — детерминированная полиномиальная сложность,
а NP — недетерминированная полиномиальная сложность.
Упрощённая классификация задач по вычислительной
сложности.
|
|
|
|
|
|
|
|
|
Advanced technologies are required for simulation of various concurrent multiagent systems such as land combat operations, aircraft combat missions, tracking and possible interception of missiles and satellites, surveillance operations, etc. Unmanned aircraft or tanks may participate in reconnaissance missions or in the full scale combat operation. Similar teams of intelligent vehicles may be dispatched by the adversary. Control of those actions requires permanent adaptation to the intermediate results and dynamic re-computation in real time.
|
|
|
Разработка новых технологий необходима для моделирования различных параллельных многоагентных систем типа операций наземного и воздушного боя, отслеживания и возможного перехвата ракет и спутников, разведывательных операций наблюдения и т.д. Беспилотные самолеты или танки могут участвовать в разведывательных миссиях или в полномасштабной боевой операции. Подобные отряды интеллектуальных транспортных средств могут участвовать и на стороне противника. Управление этими действиями требует постоянной адаптации к промежуточным результатам и динамическому пересчёту в режиме реального времени.
|
|
|
One example is the problem of real time control of the air combat in which a number of planes (manned or unmanned) equipped with countermeasures evade a number of pursuers equipped with missiles. Another example is the problem of optimal control of unmanned aerial vehicles (UAVs) that are in the reconnaissance flight to locate mobile missile launchers. The actual launch points are usually detected by satellite-based sensors. The UAVs use detected launch points to initiate their search, locate and possibly destroy them. In the real world scenario, the UAVs control should be considered together with the air combat when UAVs evade a pursuing enemy aircraft and, on their turn, pursue adversarial mobile launchers. Similar problems of the development and real time replanning of the combat scenarios are essential for the navy and army battlefields.
|
|
|
Ещё один пример - это задача управления в режиме реального времени воздушным боем, в котором группа самолётов (пилотируемых или беспилотных), оснащённых защитными средствами, уклоняется от группы преследователей, оснащённых ракетами. Другой пример - это задача оптимального управления беспилотными самолётами (UAV), которые барражируют в разведывательном полёте, чтобы определить местонахождение подвижных пусковых установок ракет. Фактические точки запуска ракет обычно обнаруживаются датчиками при помощи спутника. UAV используются для того, чтобы, зная координаты этих точек, найти подвижные установки и, по возможности, уничтожить их. В сценарии из реальной жизни управление UAV нужно рассматривать вместе с воздушным боем, когда UAV уклоняются от преследующих их самолетов врага и, в свою очередь, продолжают поиск подвижных пусковых установок противника. Подобные задачи генерации и перепланирования боевых сценариев в режиме реального времени существенны также для морских и наземных операций.
|
|
|
Conventional models of combats can achieve computational and, sometimes, analytical solutions for the simple cases. Real world cases employing those approaches are, however, computationally intractable.
|
|
|
Традиционные модели боевых операций могут быть вычисляемы и даже могут иногда иметь аналитические решения в простых случаях. Однако, в реальных ситуациях при использовании традиционных подходов эти задачи в вычислительном отношении неразрешимы.
|
|
|
Space combat simulation problems are, in general, similar to the other combat simulations. However, the astrodynamics of the spacecraft makes these problems significantly more complex. Another factor is the vehicle’s autonomy. While the autonomy of the land, navy, and aerial vehicles is highly desirable, it is essential for the spacecraft, especially, if they are far away from Earth. Simulation and control of the two-three spacecraft combat requires enormous amounts of computations. Problems with greater number of vehicles are computationally intractable (Shinar, 1990; Garcia-Ortiz, et al., 1993).
|
|
|
Задачи моделирования космического боя, в общем-то, подобны другим задачам боевого моделирования. Однако, астродинамика космического корабля делает эти задачи значительно более сложными. Другой фактор - автономность транспортного средства. В то время как автономность наземных, морских и воздушных транспортных средств очень желательна, она просто необходима для космического корабля, особенно если он далеко от Земли. Моделирование и управление боем двух-трёх космических кораблей требует огромного количества вычислений. Задачи с ещё большим числом транспортных средств в вычислительном отношении неразрешимы (Шинар, 1990; Гарсия-Ортиз и др., 1993).
|
|
|
Another class of problems is related to intelligent manufacturing in industrial environment. Groups of robots move around the plant, collect assembly parts, deliver them to the assembly line, and assemble the product. Because of the localized control, robots collaborate only within their groups. Various groups compete with each other for common resources including parts, movement paths, assembly queue, etc. Planning of these activities requires an enormous amount of computation employing conventional approaches.
|
|
|
Другой класс задач связан с организацией работы интеллектуальных автоматов в индустриальной среде. Группы роботов перемещаются по заводу, комплектуют сборочные детали, подают их на сборочный конвейер и собирают изделие. В результате намеренно локализованного управления, роботы сотрудничают только в пределах своих групп. Различные группы конкурируют друг с другом за общие ресурсы, включая детали, пути движения, очерёдность сборки и т.д. Планирование этих действий требует огромного количества вычислений при использовании традиционных подходов.
|
|
|
Problems of software re-engineering require conversion of unstructured programs into the object-oriented software where, sometimes, the end product of such conversion must be provably correct. This conversion is intended to transform original unstructured, the so-called legacy software, into a product which must be maintainable. This class of problems can be reduced to the problems of graph transformation where the original graph represents the software to be converted. Typically, this is done employing graph-rewriting systems. While small-scale software is convertible, an attempt to scale up to the real world software poses a tremendous computational challenge.
|
|
|
Задачи конверсии программного обеспечения (ПО) требуют преобразования неструктурированных программ в объектно-ориентированное ПО, причём, иногда требуется, чтобы конечный результат такого преобразования был доказуемо правильной программой. Цель этой конверсии состоит в преобразовании неструктурированного оригинала, так называемого наследуемого ПО, в изделие, которое можно сопровождать (т.е. вносить в него изменения) в течение его жизненного цикла. Этот класс задач может быть сведен к задачам преобразования графа, где первоначальный граф представляет ПО, которое нужно конвертировать. Как правило, для этого используются системы переделки графов (graph-rewriting systems). В то время как ПО небольшого размера конвертируемо, попытка перейти к конверсии реального полномасштабного ПО сталкиваются с непреодолимыми вычислительными трудностями.
|
|
|
Problems of network security, integrity, and problems of the Internet cyberwar have recently attracted significant attention. The question is how to protect the national computer network from an attack of billions of computer viruses and worms? Which nodes and even branches should be cut off (sacrificed), which should be revitalized by activation of duplicates, what countermeasures should be engaged? A conventional response to this threat is by local protection. It appears that the amount of computation required to generate a strategy for global protection makes this problem intractable.
|
|
|
Задачи безопасности и целостности компьютерных сетей и проблемы кибервойны в Интернете недавно привлекли всеобщее внимание. Вопрос состоит в том, как защитить национальную компьютерную сеть от нападения миллиардов компьютерных вирусов и червей? Какие узлы и даже ветви должны быть отключены ("пожертвованы"), какие из них следует заново подключить ("оживить") путём активизации дубликатов, какие контрмеры должны быть приняты? Традиционный ответ на эту угрозу - локальная защита. Очевидно, что количество вычислений, необходимых для генерации стратегии для глобальной защиты делает эту задачу неразрешимой.
|
|
|
Scheduling problems with resource allocation are ubiquitous. They include scheduling jobs in industrial environment by selecting them from the queue of demands and by delivering resources to job location. Usually, not all the demanded jobs can be scheduled because of the shortage of resources while the number of demands can exceed thousands. How to schedule the most important jobs in order to obtain the best schedule? One of such problems is scheduling of maintenance of power units in a number of power plants. Each maintenance requires the unit to be shut down and, consequently, to compensate the loss of power by the power reserve from other power plants. These problems are known to be, in general, computationally intractable (Garey and Johnson, 1991).
|
|
|
Задачи составления расписаний с распределением ресурсов встречаются повсюду. Они включают составление графика различных операций в индустриальной среде в соответствии с очередью заявок и доставку требуемых ресурсов по месту конкретной операции. Обычно, не все заявки могут быть удовлетворены из-за нехватки ресурсов, в то время как число заявок может достигать тысяч. Как выделить самые важные заявки, чтобы получить лучший график? Одна из таких задач - это задача составления графика ремонтов генерирующего оборудования электростанций. Вывод генератора в ремонт требует, чтобы он был остановлен и, следовательно, необходимо компенсировать потерю его мощности из запасов мощности на других электростанциях. Подобные задачи, как известно, в общем случае в вычислительном отношении неразрешимы (Гэри и Джонсон, 1991).
|
|
|
Programming the game of chess is not necessarily practical but certainly a challenging problem. It is most attractive because, in contrast with many others, true human experts like grandmasters and world champions do exist. Some of them are capable of the analysis by introspection and by comparison with the computer game models. This gives us a chance of successful discovery and formalization of their approach, and the possible transfer to different problem domains.
|
|
|
Программирование игры в шахматы - это вовсе не обязательно важная для практики, но конечно стимулирующая и трудная задача. Она особенно привлекательна потому, что в отличие от многих других задач в шахматах истинные эксперты действительно существуют - это гроссмейстеры и шахматные чемпионы. Некоторые из них способны к анализу путём самонаблюдения и сравнения своего видения с компьютерными моделями игры. Это даёт нам шанс на успешное распознавание и формализацию их подхода с возможным его использованием в других проблемных областях.
|
|
|
|
|
|
|
|
|
Problems of long and short-range mission planning, especially for autonomous navigation, aerospace robot control, such as UAV, aerospace combat operations control, global and local reconnaissance, etc., are usually described mathematically in the form of pursuit-evasion differential games. The classic approach based on the conventional theory of differential games (Isaacs, 1965) is insufficient, especially in case of dynamic, multiagent models (Lirov, Rodin et al., 1988; Garcia-Ortiz, et al., 1993). It is well known that there exists a small number of differential games for which exact analytical solutions are available. There are a few more for which numerical solutions can be computed in a reasonable amount of time, under rather restrictive conditions. However, each of these games must be one-to-one, which is very far from the real world combat scenarios. They are also of the "zero-sum type" which does not allow a new agent to join the game or some of the agents of both sides to be disengaged. Other difficulties arise from the requirements of the 3D modeling, limitation of the lifetime of the agents, or simultaneous participation of the heterogeneous agents such as on-surface, undersea, and aerospace vehicles.
|
|
|
Задачи планирования ближних и дальних миссий, особенно для автономной навигации, управления космическим роботом (типа UAV), управления операциями космического боя, глобальной и локальной разведки и т.д. обычно описываются математически в форме дифференциальных игр уклонения от преследования. Классический подход, основанный на традиционной теории Дифференциальных Игр (Айзекс, 1965) недостаточен, особенно в случае динамических, многоагентных моделей (Лиров, Родин и др., 1988; Гарсия-Ортиз и др., 1993). Известно, что при классическом подходе существует небольшое количество дифференциальных игр, для которых построены точные аналитические решения. Есть ещё несколько классов дифференциальных игр, для которых численные решения могут быть получены за разумное время при весьма ограничивающих условиях. Однако каждая из этих игр должна быть типа "один против одного", что, естественно, далеко от реальных боевых сценариев. Кроме того, эти игры являются играми с "нулевой суммой", что не позволяют новому агенту "войти" в игру или некоторым агентам обеих сторон быть исключёнными. Другие трудности связаны с потребностью в трёхмерном (пространственном) моделировании с ограничениями на время жизни агентов или с одновременным участием разнотипных агентов, например, поверхностных, подводных или космических транспортных средств.
|
|
|
Following (Rodin et al., 1987, 1988; Rodin, 1988; Shinar, 1990), discrete-event modeling of complex control systems can be implemented. These techniques can be based on generating geometrically meaningful states. By discretization time, a finite game tree can be obtained. The nodes of the tree represent the states of the game, where the players can select their controls for a given time increment. It is also possible to distinguish the respective moves of the adversarial sides (including simultaneous actions). Thus, the branches of the tree are the moves in the game space, and these problems can be viewed as planning problems in AI. The main difficulty is the combinatorial explosion of the search tree. According to (Lirov, Rodin et al., 1988) “... In the case of the two-plane game, the problem of model choice is not too great, so an exhaustive search for the best model can be performed in a reasonable amount of time. However, the search problem becomes a primary concern when ever all planes are participating in the game or, in a more complicated example, some other objects are introduced, such as obstacles at some future times”.
|
|
|
Следуя профессору Родину (Родин и др., 1987, 1988; Родин, 1988; Шинар, 1990) - это может быть реализовано с помощью дискретно-событийного моделирования Сложных Систем управления. Эти методы могут быть основаны на генерации состояний, имеющих геометрический смысл. Конечное дерево игры (ДИ) может быть получено путём дискретизации времени. Узлы дерева будут представлять состояния игры, в которых игроки смогут выбирать своё управление для каждого временного интервала. Также, можно будет определить ходы, соответствующие противоборствующим сторонам (включая одновременные действия). Таким образом, ветви дерева будут представлять последовательности ходов в пространстве игры, а сами задачи могли бы рассматриваться как проблемы планирования в ИИ. Главная трудность - комбинаторный взрыв дерева перебора (ДП). Согласно (Лиров, Родин и др., 1988) “...в случае игры с двумя самолетами задача оптимального выбора не является слишком трудной, так что исчерпывающий перебор в поисках лучшей модели может быть выполнен за разумное время. Однако проблема перебора начинает вызывать особое беспокойство, если вдруг все самолёты примут участие в игре одновременно или, в более сложном примере, когда другие объекты, например препятствия, могут быть введены в игру в будущем”.
|
|
|
How do we handle this combinatorial explosion? Can we reduce an average number of alternatives considered in each position (state), ultimately, to one alternative? This would be an ideal algorithm, one that is able to find a solution without any tree-based search.
|
|
|
Как бороться с комбинаторным взрывом? Можем ли мы уменьшить среднее число альтернатив, которые рассматриваются в каждом состоянии (позиции), в конечном счёте, доведя их до одной альтернативы? Идеальным был бы алгоритм, способный найти решение вообще без перебора на дереве ходов.
|
|
|
The branching factor B is a parameter representing the average breadth of the search tree. It shows how many moves (on the average) should be included in this tree at each node. For example, in the game of chess applying the brute force search algorithm, we have to include all the legal moves (permitted in every position according to chess rules). This means that we have to generate a search tree of the size T which can be calculated following (1.2.1). In this equation, B is the average number of moves in each position, L is the depth of the search (assuming all the branches are terminated at the depth L), and T is the total number of positions generated. The computation of B is based on the consideration of a hypothetical search tree with the depth of all branches equal to L, total number of moves equal to T, and a constant number of successors of each node.
|
|
|
Пусть коэффициент ветвления B - параметр, представляющий среднюю ширину ДП в каждом узле. Он показывает, сколько ветвей (ходов) в среднем должно выходить из каждого узла ДП. Например, в шахматных программах, использующих алгоритмы перебора по методу «брут форс», в каждом узле рассматриваются все возможные ходы (т.е. разрешённые в позиции шахматными правилами). Это означает, что мы должны генерировать ДП с числом узлов T, которое может быть рассчитано по формуле (1.2.1). В этом уравнении B - среднее число ходов из каждой позиции, L - глубина перебора (предполагается, что все ветви усечены до глубины L) и T - общее количество построенных позиций (узлов). Вычисление B основано на рассмотрении гипотетического ДП с глубиной всех ветвей равной L, общим количеством узлов равным T при постоянном числе потомков у каждого узла.
|
|
|
By definition (Nilsson, 1980; Rich and Knight, 1991), this constant number is equal to the branching factor B and is determined as a solution of the equation (1.2.1) for given L and T relative to B. Greater values of B correspond to a non-selective search; obviously they indicate an exponential growth of the search with a big base. Algorithms that reduce B, especially those algorithms which make B close to 1, should be considered as extremely goal-driven with minimal branching to different directions.
|
|
|
По определению (Нильсон, 1980; Рич и Найт, 1991) это постоянное число равно коэффициенту эффективного ветвления B и определяется как решение уравнения (1.2.1) для заданных L и T относительно B. Большие значения B соответствуют неизбирательному перебору. Очевидно, что большое значение B указывает на рост ДП по экспоненциальному закону с большим основанием степени. Алгоритмы, которые уменьшают B, особенно те алгоритмы, которые делают B близким к 1, нужно рассматривать как наилучшие, направленные "прямо" к цели, с минимальным ветвлением в других направлениях.
|
|
|
Employing (1.2.1) for the total number of moves T actually generated during the search and the value L of the required depth of the search, we can calculate the branching factor B for an arbitrary search algorithm. It can be found as an approximate solution of the equation (1.2.2) with respect to B. This is a non-linear equation and, usually, it is being solved by various methods including the trial and error approach.
|
|
|
Используя уравнение (1.2.1) для значения T - общего количества узлов, которые фактически построены в процессе перебора и значение L - требуемой глубины перебора, мы можем вычислить коэффициент ветвления B для произвольного переборного алгоритма. Коэффициент эффективного ветвления B можно найти как аппроксимацию решения уравнения (1.2.2) относительно B. Это нелинейное уравнение и его можно решить различными методами, включая метод проб и ошибок.
|
|
|
B + B2 + ... + B L = T
|
(1.2.1)
|
|
or
|
|
B L+1 - 1
————— = T .
B - 1
|
(1.2.2)
|
|
|
B + B2 + ... + B L = T
|
(1.2.1)
|
|
или
|
|
B L+1 - 1
————— = T .
B - 1
|
(1.2.2)
|
|
|
Various search algorithms, such as dynamic programming and branch-and-bound algorithms, were constructed in order to reduce the branching factor. For the two-player opposing games, such as the game of chess, the most popular algorithms are various search algorithms with formal alpha-beta pruning (Nilsson, 1980; Rich and Knight, 1991). They are implemented in the most powerful computer chess programs, e.g., in all the programs which are current and former World Computer Chess Champions. It was proved that in the best case the alpha-beta search algorithm can reduce the number of terminal nodes to be visited as follows (Slagle and Dixon, 1969; Knuth and Moore, 1975):
|
|
2B L / 2 - 1 ,
|
is L - even ,
|
|
|
B( L+1) / 2 + B( L-1) / 2 - 1 ,
|
is L - odd .
|
This number of nodes has to be searched in any case, even with perfect move-ordering procedure. All the various modifications of the alpha-beta search can do no better than this best case (Kaindl, 1990). However, the tree still grows exponentially, albeit with a reduced exponent. The perfect ordering can theoretically double the search depth (during the same time frame) employing the reduced branching factor to approximately
√B. Through this book we use
√B, as a value of the reduced branching factor in our comparison of the alpha-beta best case results with the results obtained employing the LG tools.
|
|
|
Для уменьшения коэффициента ветвления были разработаны различные переборные алгоритмы типа динамического программирования и метода ветвей и границ. Для антагонистических игр двух игроков (типа шахмат) самые популярные алгоритмы - это различные алгоритмы перебора с формальным альфа-бета отсечением (Нильсон, 1980; Рич и Найт, 1991). Они реализованы в самых сильных шахматных программах, включая действующих и экс-чемпионов мира по компьютерным шахматам. Было доказано, что в лучшем случае алгоритм альфа-бета перебора может уменьшить число терминальных узлов в дереве перебора следующим образом (Слэйгл и Диксон, 1969; Кнут и Мур, 1975):
|
|
2B L / 2 - 1 ,
|
если L - чётно,
|
|
|
B( L+1) / 2 + B( L-1) / 2 - 1 ,
|
если L - нечётно.
|
Это число узлов должно быть просмотрено в любом случае, даже при оптимальном упорядочении ходов. Все различные модификации альфа-бета перебора не могут улучшить этот результат (Кэйндл, 1990). Однако, при альфа-бета переборе число узлов ДП растёт всё ещё по экспоненциальному закону, хотя и с меньшим основанием. Теоретически при альфа-бета отсечении на ДП можно удвоить глубину перебора (за то же самое время счёта), если оптимально упорядочить ходы в узлах ДП. Это упорядочение приводит к уменьшению коэффициента ветвления примерно до
√B. В этой книге мы используем
√B, как значение уменьшенного коэффициента ветвления, в нашем сравнении результатов альфа-бета перебора, получаемых в самом благоприятном случае, с результатами применения средств LG.
|
|
|
Assume that an arbitrary chess position, on average, contains about 40 legal moves, then alpha-beta pruning can reduce this number to approximately
6 (≈√40). Still, we have an exponential growth with a very high base
B=6 (high branching factor). As a result, chess problems that require a deep search, for example, to the depth of
L=20 or more moves, need enormous amounts of processing time to be solved. Even the Deep Blue hardware-software system cannot make this leap (Hsu, et al, 1990; Newborn, 1996, 1997). This massively parallel system of special-purpose chess chips with a processing speed of two hundred million positions per second fall short in an attempt to overcome the exponential growth that comes with a high branching factor. In real world problems the number of alternatives is far greater than 40, while required depth sometimes exceeds hundreds of moves. Even future super-computers will not be able to handle this amount of computations employing conventional search procedures.
|
|
|
Предположим, что произвольная шахматная позиция в среднем содержит примерно 40 ходов по правилам, тогда альфа-бета отсечение может уменьшить это число примерно до
6 (≈√40). Однако мы всё ещё имеем рост по экспоненциальному закону с очень большим основанием степени
B=6 (т.е. коэффициентом ветвления). В результате, шахматные задачи, которые требуют глубокого перебора, например до глубины
L=20 или больше ходов, требуют и огромного количества времени для получения решения. Даже специализированная программно-аппаратная система Дип Блю не способна преодолеть это препятствие (Хсу и др., 1990; Ньюборн, 1996, 1997). Эта массово-параллельная система из шахматных чипов специального назначения со скоростью вычислений до двухсот миллионов позиций в секунду не способна противостоять росту ДП по экспоненциальному закону с большим коэффициентом ветвления. В задачах из реальной жизни число альтернатив намного больше 40, в то время как требуемая глубина перебора может превышать сотни ходов. Даже суперкомпьютеры будущего не смогут произвести такое количество вычислений при использовании традиционных процедур перебора по методу «брут форс».
|
|
|
One of the basic approaches is to decrease the dimension of the complex system following the approach of a human expert in the field, by breaking the system into smaller subsystems. This process of decomposition can be applied recursively until we end up with a collection of basic subproblems that can be treated (in a sense) independently. This can be viewed as planning in presence of subgoals, macro-operators, and abstraction (Korf, 1987; Tate, Hendler and Drummond, 1990). At each level of decomposition we can apply an abstraction by initially ignoring the low-level details and concentrating on the essential features of the problem, addressing the details later. To a certain degree, human experts usually establish subgoals (and reach them) because they know what sequence of operators (macro-operator) to apply to reach the next subgoal. The idea of abstraction in human problem-solving was pointed out in (Polya, 1945), later, it was used in the planning version of GPS (Newell and Simon, 1972). Since then, similar ideas have been developed in many systems within formal theories of linear and nonlinear planning (e.g., Sacerdoti, 1974, 1975; Stefik, 1981; Chapman, 1987; Knoblock, 1990; Georgeff, 1990; McAllester and Rosenblitt, 1991) or within different approaches (Mesarovich and Takahara, 1989; Albus, 1991).
|
|
|
Один из основных подходов к сокращению перебора - это метод уменьшения размерности Сложной Системы путём её декомпозиции на меньшие подсистемы, используемый экспертами в различных областях. Процесс декомпозиции может быть применён рекурсивно, пока мы не получим группу базовых подзадач, которые можно рассматривать (в некотором смысле) независимо друг от друга. Всё это сродни планированию в присутствии подцелей, макрооператоров и абстракций (Корф, 1987; Тэйт, Хендлер и Драммонд, 1990). На каждом уровне декомпозиции мы можем применять абстракцию, т.е. первоначально игнорировать детали низкого уровня и сконцентрироваться на существенных особенностях задачи, а к деталям мы сможем вернуться позже. В некотором смысле, эксперты обычно устанавливают подцели (и достигают их), потому что они знают какую последовательность операторов (т.е. макрооператор) применить, чтобы дойти до следующей подцели. Идея абстракции при решении задач человеком была указана в работе (Пойа, 1945), позже она использовалась в версии Универсального Решателя Задач (GPS), предназначенной для планирования (Ньюэлл и Саймон, 1972). С тех пор подобные идеи были применены во многих системах в рамках формальных теорий линейного и нелинейного планирования (например, Сакердоти, 1974, 1975; Штефик, 1981; Чэпман, 1987; Кноблок, 1990; Георгев, 1990; Мак-Аллистер и Розенблит, 1991) или в рамках других подходов (Месарович и Такахара, 1989; Эльбас, 1991).
|
|
|
Real world complex systems usually involve dynamic processes beyond the control of a single agent. The problem solver should reason about actions that the agent has no control over and that may or may not occur concurrently with what the agent is doing. A number of theories of planning for multiagent domains have been developed in (Allen, 1984; Georgeff, 1983, 1990; McDermott, 1985; Pelavin and Allen, 1986). In particular, an event type can be considered as a set of state sequences, representing all possible occurrences of the event in all possible situations, which might include concurrent actions of multiple agents. One of the possible approaches is to approximate concurrent activity by using an interleaving approximation (Georgeff, 1983; Pednault, 1987). We use the same approximation in our first examples (Chapters 3, 4, 5, and 6). Of course, it is not possible to model simultaneous events within this approach, and we introduced true concurrency to handle that (Stilman, 1995d, 1997a; Skhisov and Stilman, 1997, 1998a, 1998b, and Chapter 6).
|
|
|
Реальные Сложные Системы обычно включают динамические процессы, которые не подконтрольны одиночному агенту. Решатель задач должен учитывать действия, неподконтрольные данному агенту, которые могут производиться последовательно или параллельно с его действиями. Различные теории планирования для многоагентных систем были предложены в работах (Аллен, 1984; Георгев, 1983, 1990; Мак-Дермот, 1985; Пелевин и Аллен, 1986). В частности, можно рассмотреть обобщённый тип события как множество последовательностей состояний, представляющее все варианты появления этого события во всех возможных ситуациях, которые могли бы включать и параллельные действия многих агентов. Один из возможных подходов - это аппроксимация параллельных действий с использованием взаимного чередования (одновременных ходов) или интерливинг-приближения (Георгев, 1983; Педнаулт, 1987). Мы используем аналогичное приближение в наших примерах в главах 3, 4, 5 и 6. Конечно, в рамках этого подхода нельзя моделировать одновременные события; для этого мы вводим истинный параллелизм (Штильман, 1995d, 1997a; Скисов и Штильман, 1997, 1998a, 1998b; и глава 6).
|
|
|
Besides a number of specific problems, including inherent the ambiguity of decision making for an agent due to immediate simultaneous actions of other agents, the major problem of one-agent planning remains and even amplifies dramatically for multiple agents. This is the problem of combinatorial explosion of the search space. Introducing concurrency by allowing moves with all the simultaneous combinations of actions results in a tremendous growth of the branching factor, and, consequently, in the growth of the search space (Chapters 6, 13, and 14).
|
|
|
Помимо множества специфических проблем, включая неопределённость, свойственную принятию решений для данного агента из-за одновременных действий других агентов, для одноагентных систем всё же остаётся основная проблема планирования, которая ещё и значительно усиливается при многих агентах. Это проблема комбинаторного взрыва пространства перебора. Представление параллелизма в виде ходов, включающих все одновременно допустимые комбинации действий, приводит к огромному росту коэффициента ветвления и, следовательно, к росту пространства перебора (главы 6, 13 и 14).
|
|
|
None of the conventional approaches to the problems considered in Section 1.1 allows us to scale up to the real world concurrent systems with respect to the number of agents, dynamic change of their capabilities, size, shape, and dimension of the operational district, concurrent actions, real time requirements, etc. One of the main difficulties is the enormous complexity of computations due to the exponential growth of the number of variants of the system’s operation to be analyzed. Fortunately, there are many such problems where the human expert skills in reasoning about complex multiagent systems are incomparably higher than the level of modern computing systems with respect to complexity reduction. Though there is no grandmaster in combat simulation or robot control, in the game of chess, the human grandmasters have achieved amazing results in search reduction. Our goal is to study human expert reasoning in the areas where the results are successful, in order to discover the keys to their success, and then apply and adopt these keys to the new, as yet, unsolved problems.
|
|
|
Ни один из традиционных подходов к задачам, которые рассмотрены в разд.1.1, не может быть масштабирован (для применения в реальных параллельных системах) по отношению к числу агентов, динамическому изменению их возможностей, их величины и формы, размерности их операционной области, к их параллельным действиям, к требованиям режима реального времени и т.д. Одна из главных трудностей - это огромная сложность вычислений из-за экспоненциального роста числа вариантов, которые должны быть проанализированы. К счастью, есть много проблемных областей, в которых способности экспертов к логическому выводу в многоагентных Сложных Системах несравненно сильнее, чем уровень современных компьютерных систем (если мы ведём речь о сокращении сложности). Хотя и нет никаких гроссмейстеров в боевом моделировании или в управлении навигацией робота, но в шахматной игре гроссмейстеры достигли удивительных результатов в сокращении перебора. Наша цель состоит в том, чтобы изучить методы эксперта при принятии решений в областях, где они приводят к успеху, чтобы обнаружить причины этого успеха, формализовать их и затем применить эти формализмы к новым, пока еще нерешённым задачам.
|
|
|
As we discussed above, one of the main search heuristics of a human expert is related to the decomposition of the system into subsystems. This decomposition has been implemented for many classes of problems with varying degrees of success. Implementations based on the formal theories of linear and nonlinear planning encounter efficiency problems. An efficient planner requires an intensive use of heuristic knowledge. On the other hand, a pure heuristic implementation can hardly be reproduced for other problem domains. Each new problem should be carefully studied and previous experience usually cannot be applied. Is there a general constructive approach to such implementations? What are the formal properties of expert’s heuristics which drove us to a successful hierarchy of subsystems for a given problem? How can we apply the same ideas for a different problem domain?
|
|
|
Как уже говорилось, одна из главных эвристик перебора, используемых экспертами, связана с декомпозицией системы на подсистемы. Декомпозиция была осуществлена для многих классов задач с различными результатами. Реализации, основанные на формальных теориях линейного и нелинейного планирования, сталкиваются с проблемами эффективности. Эффективный планировщик требует интенсивного использования эвристических знаний. С другой стороны, чисто эвристическая реализация специфичная для одной области, едва ли может быть воспроизведена в других проблемных областей. Каждая новая задача требует тщательного изучения, а предыдущий опыт обычно не может быть использован. Существует ли общий конструктивный подход для выхода из этого тупика? Каковы формальные свойства экспертных эвристик, которые привели нас к успешной иерархии подсистем в данной задаче? Как применить те же самые идеи в другой проблемной области?
|
|
|
We need formal language tools for an adequate representation of expert skills. An application of such tools to the area of successful results achieved by the human expert should yield a formal, domain-independent knowledge ready to be transferred to different areas. Neither natural nor programming languages satisfy our goal. The first are informal and ambiguous, while the second are usually detailed, lower-level tools. We have to learn how we can formally represent, generate, and investigate a mathematical model based on the abstract images extracted from the expert’s vision of the problem.
|
|
|
Нам потребуются формально-языковые средства для адекватного представления навыков экспертов. Применение таких средств в области, где эксперты уже достигли успешных результатов, должно привести к разработке формальных знаний, независящих от проблемной области, которые можно будет применить в других областях. Ни естественные языки, ни языки программирования не удовлетворяют этой цели. Первые - неформальны и неоднозначны, в то время как вторые - обычно чересчур детализированы средствами низкого уровня. Мы должны понять, как формально представить, сгенерировать и исследовать математическую модель, основанную на абстрактных образах, извлекаемых из видения задачи экспертом.
|
|
|
|
|
1.3 LG Approach at first Glance
|
|
|
|
Linguistic Geometry (LG) includes the syntactic tools for knowledge representation and reasoning about multiagent complex systems. LG has been developed as a generic approach for a certain class of complex systems. This approach gives us powerful tools for reducing the search in different complex problems by decomposing the complex system into a hierarchy of dynamic interacting subsystems. LG allows us to study this hierarchy formally, investigating its general and particular properties. These tools provide a framework for the evaluation of the complexity and quality of solutions, and for generating computer programs for specific applications.
|
|
|
Лингвистическая Геометрия (LG) включает синтаксические инструменты для представления знаний и логического вывода в многоагентных Сложных Системах. LG была разработана как общий подход для некоторого класса Сложных Систем. Этот подход предоставляет мощные инструменты для сокращения перебора в различных задачах путём декомпозиции Сложной Системы в динамическую иерархию взаимодействующих подсистем. LG позволяет изучать эту иерархию формально, исследуя её общие и специфические свойства. LG-инструменты предоставляют методику для оценки сложности и точности решений, а также для разработки компьютерных программ - приложений LG к различным прикладным областям.
|
|
|
The purpose of LG is to provide solutions to a variety of problems with huge state spaces, where it is desirable to find optimal or "the best you can do" behavior of entities generating purposeful transitions from state to state. Such problems include cooperation/competition of teams of intelligent (or human guided) robots (e.g., for ground or seagoing vehicles, aircraft, or spacecraft); safety-critical control systems for the remote fully automatic objects like planetary exploration vehicles; VLSI design; planning, scheduling, and resources distribution; chess, etc. Traditionally, finding optimal or near-optimal behavior of entities for the above systems required searches for suitable branches in giant game trees. Such searches are often beyond capabilities of modern and conceivable future computers. The LG approach dramatically reduces the size of the search trees, thus making the problems computationally tractable. Although discrete by its nature, the LG approach could also be applied to the control of continuous processes described by ordinary or partial differential equations, albeit after a discretization of the equations.
|
|
|
Цель LG состоит в том, чтобы решать разнообразные задачи с огромными пространствами состояний при условии, что мы ищем "по возможности оптимальное или лучшее" поведение агентов, которые генерируют целенаправленные переходы из одного состояния в другое. К таким задачам относятся сотрудничество или противоборство команд интеллектуальных (или управляемых человеком) роботов (т.е. сухопутных или морских транспортных средств, самолётов или космических кораблей); критичные к безопасности системы управления удалёнными автоматическими объектами, подобные тем, что используются для исследования других планет; проектирование VLSI; долгосрочное планирование, составление расписаний и распределение ресурсов; шахматы и т.д. Традиционно, поиск оптимального или почти оптимального поведения объектов для вышеупомянутых систем требует полного перебора ветвей в гигантском дереве перебора (ДП). Такой перебор часто превышает (по ресурсам времени и памяти) возможности современных и даже мыслимых компьютеров будущего. LG-подход существенно уменьшает размер ДП, делая задачи решаемыми. Хотя дискретность заложена в природе LG, этот подход может быть применён и к управлению непрерывными процессами, которые описываются обыкновенными дифференциальными уравнениями или уравнениями в частных производных после их дискретизации.
|
|
|
One of the unique features of the LG approach is the formalization and utilization of search heuristics developed by highly-skilled human experts (including chess grandmasters). These experts have developed sophisticated and successful strategies resulting in tremendous search reduction in their domains. However, before the present work, the methods behind the experts’ heuristics and intuition were not understood by the AI scientists or even by the experts themselves. Based on the theory of formal languages, geometrical insight, and the powerful apparatus of modern formal logic, we formalized and generalized these heuristics, thus enabling them to be applied to a vast class of problems. Prior to this work, most of these problems were not considered by experts to be in the areas of applicability of their heuristics.
|
|
|
Одна из уникальных особенностей подхода на основе LG - это формализация и использование эвристик перебора, разработанных высоко квалифицированными экспертами (включая шахматных гроссмейстеров). Эти эксперты разработали сложные, но очень удачные стратегии, приводящие к значительному сокращению перебора в соответствующих областях. Однако, до публикации этой работы эвристические методы и интуиция экспертов, связанных с переборными задачами, были непонятны ни специалистам по ИИ, ни самим экспертам. Основываясь на теории формальных языков, геометрическом подходе и мощном аппарате современной формальной логики, мы формализовали и обобщили экспертные эвристики, сделав их применимыми к обширному классу задач. До появления LG большинство задач этого класса, как полагали сами эксперты, не находилось в областях применимости их эвристик.
|
|
|
The results of comparison of the LG approach with other methods are roughly sketched in Fig.1.1. Three different search trees are shown. The top triangle reflects the search tree to be generated employing the brute force Search. Due to the high branching factor this tree is wide. However, because time is limited, all the branches must be terminated (for example, at the same depth). The tree generated by applying alpha-beta search algorithm is deeper and narrower. This is the result of cutoffs that allow us to reduce the branching factor and search deeper branches within the same processing time. It is proved that the optimal branch will not be pruned; it will be the same as in case of the brute force search with the same depth (Knuth and Moore, 1975). However, even in this case, the exponential growth with significant branching factor does not allow us to solve most real-world problems. The third, a very narrow and deep tree reflects the LG-search the branching factor is either close to one or exactly one. It has also been proved that for certain classes of problems the LG algorithm is a winning (draw) strategy (Chapter 13).
|
|
|
Результаты сравнения LG-подхода с другими методами приведены на рис.1.1. Показаны три различных ДП. Верхний треугольник обозначает дерево, которое будет построено при использовании перебора по методу «брут форс». Широта этого дерева отражает высокий коэффициент ветвления. Однако, поскольку время ограничено, все ветви должны быть прерваны на небольшой глубине (например, на одной и той же). Дерево, построенное с применением алгоритма альфа-бета перебора, является более глубоким и более узким. Это - результат отсечений, которые позволяют уменьшить коэффициент ветвления и строить более глубокие ветви за то же самое время. Доказано, что оптимальная ветвь не будет отсечена, она будет той же, как в случае перебора по методу «брут форс» с такой же самой глубиной (Кнут и Мур, 1975). Однако, даже в этом случае рост перебора по экспоненциальному закону с большим основанием степени (коэффициентом ветвления) не позволяет нам решать большинство задач из реальной жизни. Третье, очень узкое и глубокое дерево отражает то, что при переборе на основе LG коэффициент ветвления равен точно 1 или близок к 1. Было также доказано, что для некоторого класса задач LG-алгоритм - это оптимальная (выигрышная или ничейная) стратегия (глава 13).
|
|

Figure 1.1 Comparison of searches for the same processing time.
|
|
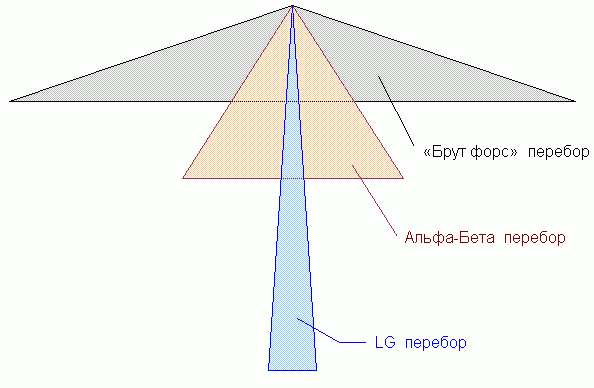
Рис.1.1 Сравнение деревьев перебора для трёх типов перебора
за одинаковое время вычислений.
|
|
|
LG approach is applicable to the concurrent multiagent systems. Who are those multiple agents? Let us introduce two types of agents. Agents of the top level, the super-agents, are fully capable of acting by means a number of mobile entities, the local agents. The environment may have a profound impact on the movements of agents. Some of the locations may be reachable in a certain number of steps, others may not be reachable at all. Consider systems with two super-agents that oppose each other. They are called the opposing sides. Usually, they pursue opposing goals. Each of them controls a team of local agents whose freedom of operation is highly restricted. Ultimately, in the examples considered in this book, the local agents do not have freedom at all and are fully controlled by a super-agent. However, the LG tools are applicable to models where the local agents are less constrained and operate autonomously with some distributed intelligence. Each super-agent develops a model of the opposing super-agent and operates assuming that the adversary will do its best within this model. The model is used for planning the agent’s actions and choosing the optimal one. The model establishes local goals for local agents. These local goals are coordinated with the global goal of the corresponding super-agent. Motions directed to the local goals are intended for a super-agent to achieve the global one. The model is dynamic: after every action, which may include concurrent movements of agents of both sides, it is updated taking into account the new situation.
|
|
|
Подход на основе LG применим к параллельным многоагентным системам. Что это за агенты? Введём агентов двух типов. Агенты высшего уровня - это суперагенты, способные к действию посредством некоторого числа подвижных объектов, т.н. локальных агентов. Окружающая среда может оказывать существенное воздействие на движение агентов. Одни пункты операционной области могут быть достижимы за некоторое число ходов, другие могут быть вовсе не достижимы. Рассмотрим системы с двумя суперагентами, которые действуют друг против друга. Они называются противоположными сторонами. Обычно эти суперагенты преследуют противоположные цели. Каждый из них управляет командой локальных агентов, чья свобода действий существенно ограничена. В конечном счете, в примерах, рассмотренных в этой книге, локальные агенты вовсе не имеют свободы и полностью контролируются суперагентом. Однако, инструменты LG применимы и к тем моделям, в которых локальные агенты менее ограничены и работают независимо по своему разумению. Каждый суперагент разрабатывает модель своего оппонента, предполагая, что тот будет действовать наилучшим образом в рамках этой модели. Модель используется, чтобы планировать действия суперагента и выбирать оптимальные. Модель устанавливает локальные цели для локальных агентов. Эти локальные цели скоординированы с глобальной целью соответствующего суперагента. Движения, направленные к локальным целям, связаны со стремлением суперагента достигнуть своей глобальной цели. Модель является динамической, т.е. после каждого действия, которое может включать и одновременные передвижения агентов обеих сторон, она обновляется с учётом новой ситуации.
|
|
|
The dynamic model can be viewed as a hierarchy of subsystems. We introduce local goals by decomposing the system of local agents into subsystems striving to attain these goals. For example, each second-level subsystem includes local agents of both opposing sides: the goal of one side is to attack and destroy another side’s local agent (a target), while the opposing side tries to protect it. In the robot control, for example, it means the selection of a pair of robots of opposing sides: one - as an attacking element, and the other - as a local target, generation of the local paths for approaching the target, as well as the paths of other robots supporting the attack or protecting the target.
|
|
|
Динамическая модель может рассматриваться как иерархия подсистем. Мы вводим локальные цели, разбивая систему локальных агентов на подсистемы, которые стремятся к достижению своей цели. Например, каждая подсистема второго уровня включает локальных агенты обеих противоположных сторон: цель одной стороны состоит в том, чтобы атаковать и уничтожить локального агента другой стороны (мишень), в то время как противоположная сторона старается его защитить. Например, в управлении навигацией робота это означает, что выбирается пара роботов противоположных сторон: один - как нападающий элемент, другой - как локальная мишень. Затем генерируются локальные пути, ведущие к мишени, а также пути других роботов, поддерживающих нападение или защищающих мишень.
|
|
|
In LG the hierarchy of subsystems is represented as a hierarchy of formal languages. To introduce formal languages following (Hopcroft and Ullman, 1979), we have to use symbols. A symbol is an abstract entity that we shall not define formally. Examples of symbols include
a,
t,
a(xi),
t(p2,
t2,
τ2),
π(i5)
etc .
A string (or word ) is a finite sequence of concatenated symbols . For example ,
a(x 1) a(x 2) ... a(x n) is a string , if
a(x 1) , a(x 2) , ... , a(x n) - are symbols . An alphabet is a finite set of symbols . A ( formal) language is a set of strings of symbols from some alphabet .
The empty set ,
, and the set { e} consisting of the empty string e - are languages . Consider a language
W and a string
w of this language . Alphabet of the string
w,
V( w) , is a set of symbols whose members occur at least once in the string w. For example , the set
V={ a(x1), a(x2), ... , a(xn) }
is the alphabet of the string a(x 1) a(x 2) ... a(x n) .
|
|
|
Иерархия подсистем в LG представлена как иерархия формальных языков. Чтобы ввести формальные языки, следуя (Хопкрофт и Ульман, 1979), мы должны использовать символы. Символ - это абстрактный объект, который мы не будем сейчас определять формально. Примеры символов включают
a,
t,
a(xi),
t(p2,
t2,
τ2),
π(i5)
и т.д .
Цепочка символов (или слово) — это конечная последовательность символов , записанных рядом друг с другом . Например ,
a(x 1) a(x 2) ... a(x n) — это слово , если
a(x 1) , a(x 2) , ... , a(x n) — символы . Алфавит — это конечное множество символов . Формальный язык — это множество слов , состоящих из символов некоторого алфавита .
Тогда пустое множество
и множество { e} , состоящее из пустого слова e, - это языки . Рассмотрим язык
W и слово
w этого языка . Алфавит
V( w) слова
w является множеством символов , элементы которого , по крайней мере , однажды встречаются в слове
w. Например , множество
V={ a(x1), a(x2), ... , a(xn) }
- это алфавит слова a(x 1) a(x 2) ... a(x n) .
|
|
|
A chart of the Hierarchy of Formal Languages is shown in Fig.1.2 as a building set of three types of triangles. Every state of the state space (the set of all positions, i.e., all possible configurations of agents) is represented by the 2-hierarchy, two embedded triangles (the Language of Trajectories and the Language of Webs). Several triangles that represent states together with their 2-hierarchies and additional attributes are embedded in one large triangle, a string of the Language of Translations. This top-level language includes a solution of the problem. A detailed presentation of the LG Hierarchy of Languages begins in Chapter 2 and continues in Chapters 8-12. A more elaborate illustration of the chart is shown in Fig.1.4. Below, we give a preliminary, brief introduction to this Hierarchy.
|
|
|
Диаграмма Иерархии Формальных Языков показана на рис.1.2 в виде множества треугольников трёх типов. Любое состояние из пространства состояний (т.е. из множества всех позиций или из всех возможных конфигураций агентов на абстрактной доске) представлено иерархией из двух вложенных треугольников (Языка Траекторий и Языка Сетей Траекторий). Несколько треугольников, которые представляют состояния (вместе с их двойной иерархией и дополнительными атрибутами), вложены в один большой треугольник - слово Языка Переводов. Этот высокоуровневый язык собственно и включает в себя решение задачи. Детальное описание Иерархии Языков в LG начинается в главе 2 и продолжается в главах 8-12. Более точная (но сложная) версия этой диаграммы показана на рис.1.4. Ниже, мы даём предварительное, краткое введение в эту Иерархию.
|
|

Figure 1.2 Hierarchy of Subsystems in LG as Hierarchy of Formal Languages.
|
|
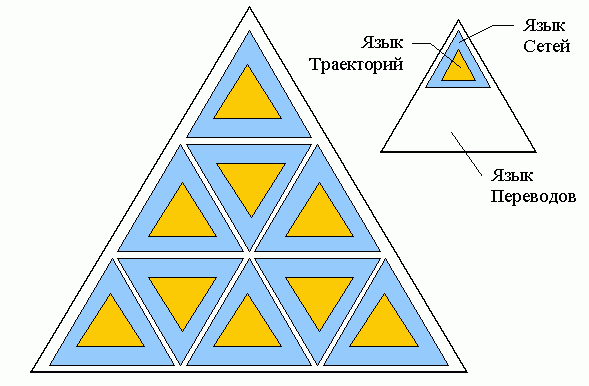
Рис.1.2 Иерархия подсистем в LG как Иерархия Формальных Языков.
|
|
|
The first-level subsystems in LG are represented by the Language of Trajectories that is the set of "trajectories", the following strings of symbols:
where
xi are called parameters. Values of parameters incorporate the semantics of problem domain. Strings of this type represent paths (trajectories) of local agents. For example, for a robotic model,
xi are the coordinates of the robot’s planning path.
|
|
|
Подсистемы первого уровня в LG представлены Языком Траекторий, который является множеством "траекторий", т.е. слов типа:
где
xi - называются параметрами. Значения параметров определяются семантикой проблемной области. Слова этого типа представляют пути (траектории) локальных агентов. Например, для модели роботов
xi - координаты планируемого пути робота.
|
|
|
The second-level subsystems in LG are represented by the Language of Webs, which is the set of "webs" or "networks", the following strings of symbols:
|
t(p1, t1, τ1) t(p2, t2, τ2) ... t(pk, tk, τk) ,
|
where
pi , ti , τi are called parameters;
pi is a local agent of the system (a robot or a software agent),
ti is an entire trajectory of the agent
pi,
a
τi is a list of domain-specific parameters. These networks represent a framework for dynamic tactical planning. The agents move along the paths (trajectories) attempting to achieve local goals, while advancing the achievement of the global goal of the super-agent, such as victory in a combat or the best schedule of a power-producing system. There may be many levels of network languages representing a hierarchy of subsystems.
|
|
|
Подсистемы второго уровня в LG представлены Языком Сетей Траекторий, который является множеством Web-сетей, т.е. слов типа:
|
t(p1, t1, τ1) t(p2, t2, τ2) ... t(pk, tk, τk) ,
|
где
pi, ti, τi - называются параметрами;
pi - это локальный агент системы (робот или программный агент),
ti - это траектория агента pi,
а
τi является списком параметров, зависящих от конкретной задачи. Эти Web-сети представляют рабочую схему для локального динамического планирования. Агенты перемещаются по траекториям, стремясь к достижению своих локальных целей, в то время как суперагент продвигается к глобальной цели, типа победы в бою или лучшего графика ремонтов электрогенераторов. Наша система может иметь несколько уровней для языков Web-сетей, представляющих иерархию подсистем.
|
|
|
The entire system operates by changing from one state to another. That is, the movement of a local agent from one point to another causes an adjustment of the hierarchy of languages. This adjustment is represented as a mapping, a translation, from one hierarchy to another, or, more precisely, to a new state of the same hierarchy. The search for a strategy generates a number of paths (sequences of moves) through the state space which can be considered as series of translations of the hierarchy of languages.
|
|
|
Полная система функционирует, переходя из одного состояния в другое, т.е. движение локального агента из одного пункта в другой вызывает изменение иерархии языков. Это изменение можно представить как отображение, т.е. перевод из одной иерархии языков в другую или, более точно, в новое состояние той же самой иерархии. При переборе ходов в поисках оптимальной стратегии мы генерируем множество путей (последовательностей ходов) в пространстве состояний; таким образом, этот перебор можно рассматривать как последовательность переводов иерархии языков.
|
|
|
In the top-level formal language in LG, the Language of Translations, every "search" is represented by a string of symbols:
where
ik are called parameters. Each symbol
π(ik), represents a move of a local agent along the network. Searches in the Language of Translations represent the actual searches for an optimal (suboptimal) operation, such as the winning strategy for a combat, the best maintenance schedule, etc. Generation in this language is controlled by interaction of networks. This generation results in a dramatically reduced search which yields a solution of a problem.
|
|
|
В LG в формальном языке высшего уровня - Языке Переводов - любой перебор представлен словом:
где ik - называются параметрами. Каждый символ π(ik) соответствует ходу локального агента по Web-сети. Перебор (вывод слова) на Языке Переводов представляется фактически как поиск оптимальной или близкой к оптимальной стратегии типа выигрышной стратегии для боя, лучшего графика ремонтов и т.д. Вывод слова в этом языке управляется взаимодействием всех Web-сетей. Результат вывода - существенно уменьшенный перебор, который и приводит к решению задачи.
|
|
|
|
|
1.4 LG Approach: Deeper Account
|
|
1.4 Углублённое рассмотрение LG-подхода
|
|
|
A class of problems to be studied are the problems of optimal operation of an LG system, a Complex System. This system is defined (DEF 2.1-2.4) as a twin set of elements (local agents) and points (locations), where elements are units moving from one point to another. It is a very general representation, e.g., in robot control problems elements are autonomous robots moving along a path (constructed of the points) through a complex hazardous 2D or 3D environment. The elements are divided into two or more opposing sides (super-agents), although, in this book, we consider only two-side systems. Each side can attack and destroy opposing elements and protect friendly elements. A destroyed element must be withdrawn from the system but it can reappear in another situation. A withdrawal happens if an attacking element comes to the point where an element of the opposing side stands. Each side aims to reach a set of specific configurations of elements. For example, this configuration may reflect a set of specific locations of friendly elements or a set of locations of elements of both sides with the maximum gain, the total algebraic value of the friendly and opposing elements destroyed and withdrawn from the system.
|
|
|
Классы задач, которые будут изучены - это задачи оптимального управления LG-системой, т.н. Сложной Системой. Эта система определена (ОПРЕДЕЛЕНИЯ 2.1-2.4) как пара множеств: множество точек (пунктов) и множество локальных агентов, которые перемещаются, двигаются из одной точки в другую. Это - очень общее представление. Например, в задачах управления навигацией робота локальные агенты - это автономные роботы, перемещающиеся по траектории (построенной из точек) в сложной и опасной двумерной или трёхмерной окружающей среде. Агенты могут быть разделены на две или более противоположные стороны (т.е. на суперагентов), хотя в этой книге мы рассматриваем только системы с двумя сторонами. Каждая сторона может атаковать, уничтожать агентов противника и защищать своих агентов. Уничтоженный агент должен быть удален из системы, но он может появиться вновь в другой ситуации. Удаление происходит, когда атакующий агент перемещается в точку, где уже стоит агент противника. Каждая сторона стремится достичь множества определённых позиций - конфигураций агентов. Например, подобная конфигурация может представлять множество точек, в которых расположены агенты обеих сторон, с максимальным выигрышем, т.е. величина алгебраической суммы стоимостей своих и чужих агентов, которые уничтожены (и удалены из системы) достигла максимума.
|
|
|
The LG system operates by moving from one system’s state to another. That is, a move of a player, being a relocation of an element of that side (player) from one point to another, causes a transition from a current system’s state to another state. For example the set of desired configurations of elements can be considered as a set of target states. Every state can be described by the list of elements (present at the state) and their locations. LG associates a hierarchy of structures with each state. A state has a structure of trajectories that are possible paths of movement of the elements which are present at the state. Each state, also, has the structure of Zones that represent all areas of local combat at the state. The structure of Zones is more complex than the structure of trajectories. The structure of Zones is based on the structure of trajectories. Thus, LG considers the structure of Zones being higher in the hierarchy than the structure of trajectories.
|
|
|
LG-система работает, переходя из одного состояния в другое, т.е. ход игрока в виде перемещения агента (одной стороны) из одной точки в другую приводит к переходу системы из текущего состояния в другое состояние. Например, множество желательных конфигураций агентов можно рассмотреть как множество целевых состояний. Любое состояние может быть описано списком агентов и их местоположением. С каждым состоянием LG связывает иерархию структур. Состояние характеризуется структурой Траекторий, которые являются возможными путями движения агентов, присутствующих в этом состоянии. Каждое состояние также характеризуется структурой Зон, которые представляют все области локального боя в этом состоянии LG-системы. Структура Зон основана на структуре Траекторий и является более сложной, чем структура Траекторий. Таким образом, LG рассматривает структуру Зон как стоящую выше в иерархии, чем структура Траекторий.
|
|
|
The hierarchy of structures was originated from the hierarchy of subsystems introduced by the highly-skilled human experts. This introduction is as follows. A one-goal, one-level LG system (for each side) should be replaced by a multi-goal, multi-level system by introducing intermediate goals and decomposing the system down into subsystems striving to attain these goals. The goals for the subsystems are specific but coordinated within the main mutual goal. For example, each second-level subsystem, called a Zone, includes elements of the two opposing sides. The goal of one side is to attack and destroy the target, while the other side tries to protect it. In the robot control problems, this means the selection of a pair of robots of opposing sides: one - as an attacking element, and the other - as a local target, generation of a path for approaching the target, as well as the paths of other robots supporting the attack or protecting the target.
|
|
|
Иерархия структур была построена на основе иерархии подсистем, введенных высококвалифицированными экспертами. Иерархия подсистем была введена следующим образом: одноуровневая LG-система с глобальными целями (по одной для каждой стороны) была заменена многоцелевой, многоуровневой системой путём введения промежуточных целей и разбиения (декомпозиции) полной системы на подсистемы, которые стремятся их достичь. Цели для подсистем различны, но подчинены общей главной цели. Например, каждая подсистема второго уровня, называемая Зоной, включает элементы двух противоположных сторон. Цель одной стороны состоит в том, чтобы напасть и уничтожить мишень, в то время как другая сторона пытается её защитить. В задачах управления навигацией робота это означает, что выбирается пара роботов противоположных сторон: один - как атакующий агент, а другой - как локальная мишень, затем генерируется путь, ведущий к мишени, а так же пути других роботов, поддерживающих атаку или защищающих мишень.
|
|
|
A hierarchy of structures is represented in LG as a Hierarchy of Formal Languages where each string of the lower level language corresponds to a symbol of the higher-level one (Section 1.3).
|
|
|
Иерархия структур представлена в LG как Иерархия Формальных Языков, где каждое слово языка низкого уровня соответствует одному символу в слове языка более высокого уровня (разд.1.3).
|
|
|
Following the LG approach, every first-level subsystem is represented as the following word, a string of symbols:
|
a(x1) a(x2) ... a(xn) ,
|
(1.4.1)
|
where each symbol
a(xi) is taken from the alphabet of symbols
{ a(xi) }. Symbol
a does not have special meaning except to link parameters
xi in a string and indicate that this string is a trajectory. Values of parameters
xi are defined by the semantics of the problem domain. Strings (1.4.1) form the Language of Trajectories (DEF 2.8). For example, for the robot control problem,
xi - are the coordinates of the basic points of the robot’s planning path. For the maintenance scheduling problem, an analogous string represents a maintenance schedule variant for a specific power unit, where
x1, x2, ... , xn correspond to the particular days of the scheduling period. Various types of trajectories are defined in Section 2.4.
|
|
|
При LG-подходе каждая подсистема первого уровня представлена как слово или цепочка символов:
|
a(x1) a(x2) ... a(xn) ,
|
(1.4.1)
|
где символы
a(xi) взяты из алфавита символов
{ a(xi) }. Символ
a не несёт смысловой нагрузки. Он предназначен для связи параметров
xi в одно слово и указания, что это слово - траектория. Значения параметров
xi определяются семантикой проблемной области. Слова типа (1.4.1) образуют Язык Траекторий (ОПРЕДЕЛЕНИЕ 2.8). Например, для задачи управления навигацией робота
xi - это координаты пунктов остановки в планируемом пути робота. Для задачи составления графика ремонтов аналогичное слово представляет собой вариант графика ремонта для определенного агрегата, причём
x1, x2, ... , xn соответствуют определённым дням в составленном графике. Различные типы траекторий определены в разделе 2.4.
|
|
|
A second-level subsystem is represented also as a string with parameters, a web:
|
t(p1, t1, τ1) t(p2, t2, τ2) ... t(pk, tk, τk) ,
|
(1.4.2)
|
where symbol
t like an
a in (1.4.1) does not have special meaning except to link parameters in a string and indicate that this string is a web. Values of parameters
(pi, ti, τi) are defined by the semantics of the problem domain and the lower level subsystems. Symbols
pi represent elements of our system (robots, power units, etc.);
ti represent trajectories (lowerlevel subsystems) of elements
pi, i.e., strings
|
a(x1pi) a(x2pi) ... a(xnpi) ,
|
included in this subsystem,
τi represent time allotted for movement along trajectory
ti.
|
|
|
Подсистема второго уровня представлена также как слово или цепочка символов с параметрами, т.е. в виде Web-сети:
|
t(p1, t1, τ1) t(p2, t2, τ2) ... t(pk, tk, τk) ,
|
(1.4.2)
|
где символ
t подобно
a в (1.4.1) не несёт смысловой нагрузки. Он предназначен для связи параметров в одно слово и указания, что это слово - Web-сеть. Значения параметров
(pi, ti, τi) определяются семантикой проблемной области и подсистем более низкого уровня. Символы
pi обозначают агентов нашей LG-системы (роботы, агрегаты и т.д.); символы
ti - обозначают Траектории (подсистемы низшего уровня) агентов
pi, т.е. слова вида
|
a(x1pi) a(x2pi) ... a(xnpi) ,
|
включённые в эти подсистемы; а символы
τi - обозначают время, выделенное для движения по траектории
ti.
|
|
|
Using strings (1.4.1), we can represent paths of system’s elements, and with the strings (1.4.2), networks of certain paths unified by the mutual goal. For example, in the robot control model such a network of planning paths represents a draft short-range plan for approaching a local goal in a hazardous environment, i.e., getting over the mobile and immobile obstacles. In the scheduling problem, it corresponds to the maintenance schedule of a certain power unit including the schedule for the provision of resources required. A set of strings (1.4.2) is called the Language of Webs (DEF 2.18). Various types of webs, the so-called Zones, are defined in Section 2.6.
|
|
|
Используя слова (1.4.1), мы можем представить пути агентов LG-системы, а слова (1.4.2) - это Web-сети из некоторых путей, объединенных общей целью. Например, в управлении навигацией робота подобная сеть планируемых путей может моделировать набросок оперативного плана для достижения локальной цели в опасной окружающей среде (с подвижными и неподвижными препятствиями). В задаче составления расписаний это соответствует графику ремонта некоторого агрегата, включая график доставки ресурсов. Множество слов (1.4.2) - называют Языком Web-сетей (ОПРЕДЕЛЕНИЕ 2.18). Различные типы Web-сетей, так называемых Зон, определены в разделе 2.6.
|
|
|
A transition to another state of the LG system causes an adjustment of the hierarchy of structures. This adjustment can be represented as a mapping (translation) to the hierarchy of structures of the other state. Actually, we can regard the change of the hierarchy of a state as that the hierarchy itself changes states. This means that at a state of the LG system the structures of associated Trajectories and Zones constitute a state of the hierarchy of structures. A directed state transition graph of a system induces a state transition graph of the hierarchy of structures.
|
|
|
Переход к другому состоянию LG-системы приводит к перестройке иерархии структур. Эта перестройка может быть представлена как отображение (перевод) в иерархию структур другого состояния. Фактически, мы можем представить изменение иерархии при переходе LG-системы из одного состояния в другое так, как будто сама иерархия структур изменяет своё состояние. Это означает, что структуры Траекторий и Зон для соответствующих состояний LG-системы образуют состояния иерархии структур. Направленный граф переходов состояний LG-системы порождает граф переходов состояний у иерархии структур.
|
|
|
LG also introduces a higher level of the hierarchy of structures which is common to all states. Such a structure represents a game subtree and the corresponding states of the system that LG strategy for a player constructs in order to compute a move. This structure is called an LG-search tree (or LG-tree). The LG-search tree includes all the play variants that LG algorithm generates on the basis of a game state at which the player should make a move. The LG tree includes a very small subset of such variants as opposed to the full game tree. Let us restrict the term LG-search tree to coincide with a subtree representing LG variants used to compute a move for a player at a state of the LG system. The LG-search tree includes sequences of moves representing (or inducing) transitions between states of the LG system. Therefore, we can introduce another tree of corresponding sequences of mappings, translations of the hierarchy of languages (that represent these states). There exists a one-to-one correspondence between these trees. Thus, we will write about the same tree naming it either a tree of moves, or a tree of translations. This tree is represented as a string that enumerates the edges (the moves) of the tree in the order of, for example, depth first search tree traversal:
π(i1) π(i2) ... π(in) in (1.4.3). The tree itself, then, can be written down as the pair of the string mentioned above, and the tuple of functions that produce the children of any tree node. Tuple functions includes a triple of functions that produce the left-most child, the left-most sibling, and the parent of any tree node. This tuple determines the signature needed to describe the algebraic structure of the tree by means of the children producing functions (DEF 2.26).
|
|
|
В LG введен ещё более высокий уровень иерархии структур, который является общим для всех состояний. Эта структура высокого уровня представляет поддерево игры (с узлами, соответствующими состояниям LG-системы), которое порождается LG-стратегией игрока при поиске очередного хода в игре. Эту структуру называют деревом LG перебора (или LG-деревом). LG-дерево включает все варианты игры, которые LG-алгоритм генерирует в том состоянии игры, в котором игрок должен сделать ход. LG-дерево включает очень маленькое подмножество вариантов в противоположность полному дереву игры (ДИ). Ограничим употребление термина LG-дерево обозначением поддерева ДИ, представляющего варианты, рассмотренные при вычислении хода игрока в исходном состоянии LG-системы. LG-дерево включает последовательности ходов, т.е. переходов между состояниями LG-системы. Поэтому, мы можем ввести другое дерево - соответствующих последовательностей отображений или переводов Иерархии Языков (которые представляют эти состояния). Существует взаимно однозначное соответствие между этими деревьями. Таким образом, мы будем говорить об одном и том же дереве, называя его деревом ходов или деревом переводов. Это дерево представлено как слово, символы которого соответствуют рёбрам дерева, занумерованным, например, в соответствии с порядком обхода дерева по методу сначала вглубь:
π(i1) π(i2) ... π(in) в (1.4.3). Это дерево, в свою очередь может быть записано как пара, состоящая из слова, упомянутого выше, и кортежа функций, которые генерируют потомков в любом узле дерева. Кортеж функций включает тройку функций, которые генерируют крайнего левого потомка, родного брата крайнего левого потомка и их родителя для любого узла дерева. Мы предполагаем, что генерация (обход) дерева происходит слева направо. Этот кортеж описывает сигнатуру, которая задаёт алгебраическую структуру дерева посредством функций, генерирующих потомков (ОПРЕДЕЛЕНИЕ 2.26).
|
|
|
Consider the following strings:
|
( π(i1) π(i2) ... π(in), functions ),
|
(1.4.3)
|
where every symbol
π(ik) represents the following three items:
- an edge (arc) of the LG-search tree,
- a move, and
- a corresponding translation.
|
|
|
Рассмотрим следующие слова:
|
( π(i1) π(i2) ... π(in), functions ),
|
(1.4.3)
|
где каждый символ
π(ik) представляет одновременно следующие три понятия:
- ребро (дуга) LG-дерева;
- ход;
- соответствующий перевод.
|
|
|
String (1.4.3) is a member of the top-level formal language, the Language of Translations (Section 2.8 and Chapter 12). Symbol
π does not have special meaning except to link parameters in a string and indicate that this string is a tree of translations. Parameters
ik are used to identify edges (arcs) of a tree. The list of functions called functions reflects links between the arcs: they are intended to support a tree data structure represented here linearly as a string of symbols. A construction of the LG tree (1.4.3) is controlled by generation and interaction of the webs (1.4.2) and trajectories (1.4.1).
|
|
|
Слово (1.4.3) - это элемент формального языка высшего уровня - Языка Переводов (разд.2.8 и глава 12). Как и ранее, символ
π не несёт смысловой нагрузки. Он предназначен для связи параметров в одно слово и указания, что это слово - дерево переводов. Параметры
ik идентифицируют рёбра дерева. Список функций, называемый functions, отражает связи между рёбрами. Эти связи предназначены для поддержки структуры данных дерева, которая представлена здесь линейно как слово или цепочка символов. Построение LG-дерева (1.4.3) управляется генерацией и взаимодействием Web-сетей (1.4.2) и Траекторий (1.4.1).
|
|
|
If LG algorithm is used by both players, a variant (or variants) that reflect application of LG strategy for both players is given by a certain branch of the LG-search tree. However, it need not be a (contiguous) substring of the string (1.4.3) of the Language of Translations. For example, consider a 4-node tree
π(1) π(2) π(3) (Fig.1.3). Edge
π(1) leads from the root R to the single child X, edge
π(2) leads to the left child of X, and edge
π(3) leads to the right child of X. The depth first search enumeration is
π(1) π(2) π(3). The substring
π(1) π(2) represents a left branch of the tree. There is another branch consisting of the sequence of edges
π(1) and
π(3), i.e.,
π(1) π(3). However,
π(1) π(3) is not a contiguous substring of
π(1) π(2) π(3).
|
|
|
Если LG-алгоритм используется обоими игроками, то вариант (или варианты) ходов, порождаемый применением LG-стратегии для обоих игроков, является некоторой ветвью LG-дерева. Однако этот вариант не обязан быть подсловом (1.4.3) в Языке Переводов, состоящим из непрерывной подцепочки символов. Например, рассмотрим дерево с 4 узлами
π(1) π(2) π(3) (рис.1.3). Ребро
π(1) ведёт от корня R к единственному потомку, который обозначен как X, ребро
π(2) ведёт к левому потомку X и ребро
π(3) ведёт к правому потомку X. При обходе сначала вглубь (слева направо) рёбра будут занумерованы в виде списка
π(1) π(2) π(3). Подслово
π(1) π(2) представляет левую ветвь дерева. Есть ещё одна ветвь, состоящая из последовательности рёбер
π(1) и
π(3), т.е. подслово
π(1) π(3). Однако это подслово
π(1) π(3) не является непрерывным подсловом для
π(1) π(2) π(3).
|
|

Figure 1.3 A 4-node tree
π(1) π(2) π(3).
|
|
Рис.1.3 Дерево с 4 узлами
π(1) π(2) π(3).
|
|
|
If the LG algorithm is used by only one player, a play arising as an application of LG strategy for that player need not be a branch of the LG tree mentioned above. The reason is that the opponent may use moves that do not belong to the variants occurring in the LG tree. Because of the LG’s sophisticated algorithm selecting the variants, the opponents moves not belonging to the variants will be usually weaker moves. Often, LG strategy will recognize the weakness in the opponent’s response when constructing the LG tree for the subsequent moves.
|
|
|
Если LG-алгоритм используется только одним игроком, то вариант игры, возникающий после применения LG-стратегии для этого игрока, не обязан быть ветвью LG-дерева, упомянутого выше. Причина состоит в том, что противник может использовать ходы, которые не входят в варианты, образующие LG-дерево. Поскольку LG-алгоритм искушён в отборе вариантов, то те ходы противника, которые не принадлежат этим вариантам, обычно будут более слабыми ходами. Однако, определить слабость ответа противника LG-алгоритм может лишь после построения нового LG-дерева для состояния, которое возникнет после этого неожиданного хода противника.
|
|

Figure 1.4 Hierarchy of Formal Languages in LG.
|
|
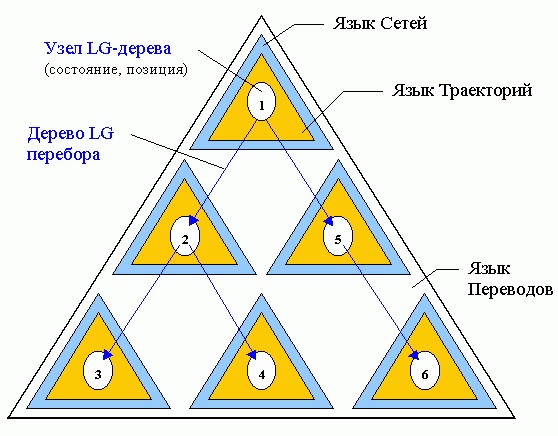
Рис.1.4 Диаграмма Иерархии Формальных Языков в LG.
|
|
|
A chart of the Hierarchy of Formal Languages is shown in Fig.1.4. This is a refinement of the chart shown in Fig.1.2. The Language of Translations is a language of trees (searches). A string of this language can be illustrated by a tree. One of such trees with 5 arcs and nodes 1-6 is shown in Fig.1.4. A node of this tree corresponds to a state of a complex system (1-6). Decomposition of the system into subsystems is represented in LG by the Hierarchy of Formal Languages. At every state the decomposition is represented by the hierarchy of two languages, the 2-hierarchy of the Languages of Webs and Trajectories. A string of the Language of Trajectories corresponds to a symbol of the Language of Webs. The 2-hierarchy is illustrated by the two embedded triangles attached to every node of the LG tree. A relationship between this hierarchy and the top-level Language of Translations (shown as one large triangle) is different from the relationship between the languages within the 2-hierarchy. A string of the Language of Translations, a search, represents an LG-search tree with nodes, that are linked to the states with attached 2-hierarchies. Therefore, the 2-hierarchies correspond to every symbol of a string of the Language of Translations. This is illustrated in Fig.1.4. An LG-search can be reflected as the generation of a string (LG tree) of the Language of Translations.
|
|
|
Диаграмма Иерархии Формальных Языков в LG показана на рис.1.4. Эта диаграмма является детализацией диаграммы, показанной на рис.1.2. Язык Переводов - это язык деревьев перебора. Слово этого языка может быть иллюстрировано деревом. Одно из таких деревьев с 5 рёбрами и узлами (1-6) показано на рис.1.4. Узел этого дерева соответствует состоянию сложной системы (1-6). Декомпозиция системы на подсистемы представлена в LG как Иерархия Формальных Языков. В каждом состоянии декомпозиция представлена иерархией двух языков - Языка Web-сетей и Языка Траекторий. Слово Языка Траекторий соответствует символу в слове Языка Web-сетей. Эта двойная иерархия иллюстрируется двумя вложенными треугольниками, присоединёнными к каждому узлу LG-дерева. Связь между этой иерархией и вышестоящим Языком Переводов (показанным как один большой треугольник) отличается от связи между языками внутри двойной иерархии. Слово Языка Переводов, т.е. перебор, представляет LG-дерево с узлами-состояниями, за которыми закреплены двойные иерархии. Поэтому, двойные иерархии соответствуют каждому символу слова Языка Переводов. Это иллюстрируется на рис.1.4. LG-перебор может быть представлен как логический вывод слова (генерация LG-дерева) в Языке Переводов.
|
|
|
The advantages of representing a decomposition of an LG system as a Hierarchy of Formal Languages become more apparent when we consider the formal mechanism for generating this Hierarchy. In pattern recognition problems, a formal linguistic approach was proposed for representation of hierarchical structured information contained by each pattern, i.e., for describing patterns by means of simpler subpatterns. This approach brings to light an analogy between the hierarchical structure of patterns and the syntax of languages. The rules controlling the merging of subpatterns into patterns are usually given by the pattern description grammars, with the power of such description being explained by the recursive nature of the grammars. Using similar approach for generating trajectories and trajectory networks, we make use of the branch of the theory of formal grammars developed in (Knuth, 1968; Rozenkrantz, 1969; Volchenkov, 1979; Stilman, 1985). A detailed account into the controlled grammars and their applications to LG is given in Chapters 8-12, 14.
|
|
|
Преимущества представления декомпозиции LG-системы в виде Иерархии Формальных Языков станут более очевидными, когда мы рассмотрим формальный механизм для генерации этой Иерархии. В задачах распознавания образов формально-лингвистический подход был предложен для представления иерархически структурированной информации, содержащейся в каждом образе, т.е. для описания образов посредством более простых подобразов. Этот подход обнаруживает аналогию между иерархической структурой образов и синтаксисом формальных языков. Правила, управляющие слиянием подобразов в образы, обычно задаются грамматиками описания образа, а мощь такого описания объясняется рекурсивной природой грамматик. Используя подобный подход для генерации Траекторий и Сетей Траекторий, мы используем раздел теории формальных грамматик, который был разработан Кнутом (1968), Розенкранцем (1969), Волченковым (1979), Штильманом (1985) и называется теорией управляемых грамматик. Детальный анализ управляемых грамматик и их приложений к LG приведен в главах 8-12, 14.
|
|
|
Recent investigation of the accuracy of the solutions generated by the LG algorithm resulted in a deeper understanding of the power of this approach. It appears that LG tools are able to implement a constructive decomposition of the state space (Chapter 13). These tools allow us to formally describe essential subsets of states and formulate intend-to-win strategies, the classes of paths in the state space leading from the Start State to the desired subset of states. Some of these strategies can be eliminated as non-implementable. The next step is an attempt of formal implementation of the non-eliminated strategies by each of the opposing sides. This is provably the best each side can do. Application of the intend-to-win strategy by each side results in the generation of a tree - the optimal solution of the search problem.
|
|
|
Недавнее исследование точности решений, полученных с помощью LG-алгоритмов, привело к более глубокому пониманию мощи этого подхода. Как выяснилось, инструменты LG способны реализовать конструктивную декомпозицию пространства состояний (глава 13). LG-инструменты позволяют нам формально описывать существенные подмножества пространства состояний и формулировать потенциально выигрышные стратегии, т.е. классы путей в пространстве состояний, ведущие из начального состояния в подмножества состояний, которые мы хотим достичь. Некоторые из этих стратегий могут быть забракованы, как нереализуемые. Следующий шаг - это попытка формальной реализации незабракованых стратегий для каждой из противоположных сторон. Это доказуемо лучшее поведение из того, что каждая сторона в принципе может сделать. Применение потенциально выигрышной стратегии для каждой стороны кончается генерацией LG-дерева, которое является оптимальным решением переборной задачи.
|
|
|
Similar ideas work for various classes of games. Optimality is proved for the classes of multiagent serial and concurrent war games with
d-dimensional operational district, a subset of
Zd. This investigation led to the new direction in LG: solving search problems by construction of strategies without any tree-based search (Chapter 13).
|
|
|
Подобные идеи работают для различных классов игр. Оптимальность доказана для классов многоагентных последовательных и параллельных военных игр с
d-мерной операционной областью действий - подмножеством
Zd. Это исследование привело к новому направлению в LG: решение переборных задач путём построения стратегий без какого-либо перебора на дереве (глава 13).
|
|
|
|
|
1.5 LG Strategies and Game Theory
|
|
1.5 LG-стратегии и Теория Игр
|
|
|
Consider the relationship between the LG strategies (for a super-agent of the LG system of two interacting super-agents) and the strategies of the game theory. Game theory emerged in the 1930s, e.g., (Von Neumann and Morgenstern, 1944), (Owen, 1982), and has a rich literature. A survey is given in (Luce and Raiffa, 1957). A significant branch of game theory is devoted to modeling economic behavior. In this branch, the goals of the players are stated by means of payoff function and by a requirement to maximize a player payoff. While LG employs an evaluation function that is a form of a payoff, the spirit of LG is closer to another branch of game theory that was initiated by Gale and Stewart (1953), and is called two player games with perfect information.
|
|
|
Рассмотрим связь между стратегиями Теории Игр и LG-стратегиями (в LG-системе из двух взаимодействующих суперагентов). Теория Игр появилась в 1930-х годах, например (Дж. фон Нейман и Моргенштерн, 1944; Оуэн, 1982) и описана в обширной литературе. Хороший обзор сделан в (Льюс и Райфа, 1957). Важный раздел Теории Игр посвящён моделированию экономического поведения. В этом разделе цели игроков сформированы с помощью функции выигрыша и требования максимизировать вознаграждение игрока. Хотя LG использует оценочную функцию, которая является формой вознаграждения, по духу LG всё же ближе к другому разделу Теории Игр, который был основан в работах (Гэйл и Стюарт, 1953) и называется теорией (бесконечных) игр 2-х лиц с полной информацией.
|
|
|
The goals of the players in two player games are stated by means of desirable sets of plays, called winning sets. A winning strategy for a player is a pattern of behavior permitting the player to attain the winning set no matter what the opponent would do. The methods of constructions differ from those of games modeling economics in employing the methods of logic, algebra, and topology, rather than of mathematical or functional analysis, and/or variational calculus. Methods similar to variational calculus are also used in another branch of game theory called differential games, (Isaacs, 1965) and Section 1.2.
|
|
|
Цели игроков в играх 2-х лиц формулируются посредством множеств желательных вариантов действий, называемых победительными множествами. Выигрышная стратегия для игрока - это такое поведения, которое приводит игрока к победе независимо от того, как ведёт себя противник. Методы построения таких стратегий отличаются от методов Теории Игр, в которых моделируется экономика, тем, что они используют методы логики, алгебры и топологии в отличие от методов математического или функционального анализа и/или вариационного исчисления, применяемых в классической Теории Игр. Методы, подобные вариационному исчислению также используются в другом разделе Теории Игр, который называется Дифференциальными Играми (Айзекс, 1965) - раздел 1.2.
|
|
|
Gale-Stewart games were extended to games over graphs due to work of A.Yakhnis and V.Yakhnis (1993) and Zeitman (1994). The earliest reference to the games over graphs are the classical papers on game theory such as (Kuhn, 1953) and (Berge, 1957). The games over graphs (1993-1994) were further extended to allow concurrent moves of more than two players (Yakhnis V. and Stilman B., 1995b). The latter games are closest to the abstract board games employed by the LG systems.
|
|
|
Игры Гэйла-Стьюарта (2-х лиц с полной информацией) были расширены до игр на графах в работах (А.Яхнис и В.Яхнис, 1993; Зейтман, 1994). Самая ранняя ссылка на игры на графах содержится в классических статьях по Теории Игр (Кун, 1953; Берж, 1957). В 1993-94 годах было сделано следующее расширение класса игр на графах, позволившее включить параллельные ходы, а также игры с более чем двумя игроками (В.Яхнис и Б.Штильман, 1995b). Введенный класс игр наиболее близок к абстрактным настольным играм (ABG) или Сложным Системам, которые моделируются LG-системой.
|
|
|
The objectives of the graph games and those of LG are not identical since within the LG approach the class of useful strategies is wider than that of winning strategies. Intuitively, the LG-specific strategies could be understood as "the-best-you-can-do" strategies, rather than winning strategies. Indeed, often the LG games do not have a "deterministic" winning strategy due to concurrent moves. As a result, the LG methods lead to new ways of constructing winning strategies. LG constructs winning strategies on the basis of mathematical artifacts that LG has discovered and distilled by formalizing the strategies of experts.
|
|
|
Цели игр на графах и цели в LG не идентичны, так как в рамках LG-подхода класс полезных стратегий шире, чем класс выигрышных стратегий. Интуитивно, специфические LG-стратегии можно рассматривать как стратегии типа "лучшие из возможных", а не как исключительно выигрышные стратегии. Действительно, часто LG-игры не имеют "детерминированной" выигрышной стратегии из-за параллельных ходов. В результате методы LG приводят к новым способам построения выигрышных стратегий. LG генерирует выигрышные стратегии на основе математических конструкций, которые были впервые введены в LG и приспособлены для формализации стратегий экспертов.
|
|
|
It is convenient to regard an LG system as a two player game where the sides (or super-agents) are the players. We will relate the notion of LG strategy for a side or a super-agent to that of a player in a two player game. Most constructions of a two player win-loss game theory are based on the concept of a game tree. This tree consists of all possible moves of players and embraces all possible plays of the game. LG attaches a state to each node (position) on the game tree. This is a state of the game, whose main content is the state of the board for the games such as chess, checkers, tic-tac-toe, etc. For the LG systems (as defined in Section 2.2) the state of the game is the state of the system.
|
|
|
Для проведения параллелей нам будет удобно рассматривать LG-систему как игру 2-х лиц, где стороны (или суперагенты) - это игроки. Мы свяжем понятие LG-стратегии для стороны или суперагента со стратегией игрока в игре 2-х лиц. Как обычно, большинство построений для игр 2-х игроков в Теории Игр основано на понятии дерева игры (ДИ). Это дерево состоит из всех возможных ходов игроков и охватывает все возможные варианты розыгрышей в игре. LG связывает с каждым узлом ДИ состояние игры. Состояние игры - это позиция на доске для игр типа шахмат, шашек, крестиков-ноликов и т.д. Для LG-систем (как определено в разделе 2.2) состояние игры - это состояние LG-системы.
|
|
|
As in the game theory LG looks for strategies for both sides (players), but makes the corresponding definitions on the basis of a state of a system (or game) rather than a game tree. The focus of LG, though, is effectively computable strategies. This is in line with constructive approach to finding winning strategies in the theory of two player games as pioneered by Buchi and Landweber (1969) and continued by Gurevich and Harrington (1982), A.Yakhnis and V.Yakhnis (1990, 1993), McNaughton (1993), and Zeitman (1994). The proximity of the goals of the latter approaches to that of LG is sometimes coincidence, where LG computes a provably winning (draw) strategy for a player (Chapter 13). Some other times, LG computes a strategy for a player which is good, but it may be difficult or intractable to see whether the strategy is winning for that player. The game theory algorithms for constructing winning strategies are usually intractable due to the exponential (or worse) running time, while the LG algorithms are practical and even polynomial-time (for subclasses of problems).
|
|
|
Как и в Теории Игр Гэйла-Стюарта, LG занимается поиском стратегии для обеих сторон (игроков), но вводит соответствующие определения на основе состояний LG-системы (или игры), а не на основе ДИ. В фокусе LG, тем не менее, оказываются эффективно вычисляемые стратегии. Это соответствует конструктивному подходу к обнаружению выигрышных стратегий в Теории Игр 2-х игроков Гэйла-Стюарта, впервые введенному Бухи и Ландвебером (1969) и продолженному Гуревичем и Харрингтоном (1982), А.Яхнисом и В.Яхнисом (1990, 1993), Мак-Нотоном (1993) и Зейтманом (1994). Близость целей последнего подхода к LG иногда проявляется в полном совпадении: речь идёт о тех случаях, когда в LG вычисляется доказуемо победная (ничейная) стратегия для игрока (глава 13). В других случаях, LG вычисляет стратегию, которая является хорошей, но может быть сложно или практически невозможно проверить, действительно ли эта стратегия является выигрышной для данного игрока. Алгоритмы Теории Игр, строящие выигрышные стратегии обычно практически неприменимы из-за экспоненциального (или ещё худшего) времени исполнения, в то время как LG-алгоритмы являются практическими и даже полиномиальными по времени (для подклассов задач).
|
|
|
Slightly paraphrasing a game theory definition of a strategy for a player over a game tree, we give a definition of an LG strategy based on a game state. A strategy of a player is a partial function over game states that produces moves for that player. A winning strategy of a player is a strategy such that if the player follows that strategy two properties are satisfied. Firstly, the strategy is defined at every state at which the player has to move and which was already produced by the use of the strategy (including the Start State). Secondly, any resulting sequences of moves of both sides lead the system from the Start State to the target states for the player, while the opposing side makes arbitrary legal moves. More details about the LG strategies are provided in Chapter 13.
|
|
|
Немного перефразируя, данное в Теории Игр, определение стратегии для игрока на ДИ, мы получим определение LG-стратегии, основанной на состояниях игры. Стратегия - это частичная функция на состояниях игры, которая генерирует ходы для этого игрока. Выигрышная стратегия игрока - это такая стратегия, которая удовлетворяет двум свойствам. Во-первых, стратегия определена в каждом состоянии, в которое игрок должен попасть, следуя ей, а также в состояниях, которые уже были сгенерированы с использованием этой стратегии, включая начальное состояние. Во-вторых, любые конечные последовательности ходов обеих сторон, сгенерированные выигрышной стратегией, приведут систему из начального состояния в целевые состояния для данного игрока, в то время как противоположная сторона может делать любые ходы, разрешённые правилами игры. Дальнейшие подробности об LG-стратегиях приведены в главе 13.
|
|
|
We defined a strategy using the game tree of all possible moves of both sides. However, the LG algorithm does not generate this tree. The LG-search procedure generates a very small subtree of the full game tree by means of generating a rather small subset of all states of a system. In Section 1.4 and further in this book, this subtree is called an LG-search tree (or a reduced search tree) as opposed to the full game tree (or a brute force search tree). It is proved that for some classes of problems, the LG-search tree includes the branches that correspond to sequences of moves generated by a winning (or draw) strategy (Chapter 13). For other classes of problems, this tree includes the branches that correspond to sequences of moves generated by the best strategy known to the experts (while any winning strategy is unknown). Also, further in this book, we will write about "trees of moves", "branches (or sequences) of moves", and "variants" (virtual plays), omitting statements about one-to-one correspondence between arcs (edges) of the trees and moves of players(sides).
|
|
|
Мы определили стратегию, используя ДИ, включающее все возможные ходы обеих сторон. Однако LG-алгоритм не генерирует это ДИ. Процедура LG-перебора формирует очень маленькое поддерево полного ДИ путём генерации маленького подмножества всех состояний системы. В разделе 1.4 и далее в этой книге, это поддерево названо LG-деревом (или сокращённым деревом перебора) в противоположность полному ДИ при поиске решения методом «брут форс». Доказано, что для некоторых классов задач LG-дерево включает ветви, которые содержат последовательности ходов, сгенерированные выигрышной (или ничейной) стратегией (глава 13). Для других классов задач это сокращённое дерево включает ветви, соответствующие последовательностям ходов, которые сгенерированны с использованием лучшей стратегии, известной экспертам (в то время как никакая (абсолютно) выигрышная стратегия вообще неизвестна). Также, далее в этой книге, мы пишем "деревья ходов", "ветви (или последовательности) ходов" и "варианты" (виртуальные розыгрыши), опуская формулировки о взаимно однозначном соответствии между рёбрами деревьев и ходами игроков.
|
|
|
The LG algorithm computes a strategy for a player by selecting the branches obtained by applying the minimax algorithm on the LG-search tree on behalf of both players. In practice, the tree generation and the minimax are combined in one procedure. In some cases, the LG tree is so small that all of its plays are won by the same player. In other words, this tree represents a winning strategy (Chapter 13) of that player with respect to the LG tree. It may or may not be the case that the strategy is winning with respect to the original game tree.
|
|
|
LG-алгоритм вычисляет стратегию игрока, выбирая ветви, полученные при применении МиниМаксного алгоритма на LG-дереве для обоих игроков. Практически генерация LG-дерева и МиниМакс объединены в одной процедуре. В некоторых случаях LG-дерево является настолько маленьким, что во всех вариантах (игры) выигрывает один и тот же игрок. Другими словами, это LG-дерево представляет выигрышную стратегию (глава 13) для данного игрока. Возможно (хотя это и не гарантировано), что найденная LG-стратегия будет выигрышной также и для полного ДИ.
|
|
|
The LG system operates by moving from one state to another. That is, a move of a player causes a transition from a current system’s state to another state. If a sequence of state transitions does not have a loop, this sequence defines a unique play on a game tree. Otherwise, there are many plays corresponding to the sequence. The plays are different only in how many times they repeat the moves that correspond to transitions in the loop(s) of the sequence of states. In other words, the plays vary in how many times they repeat the loop(s). The important fact is that the state transition system of an LG system of agents is a graph rather than a tree. However, the important decisions on whether the game terminates or who wins the game, are based on the states of the state transition system, rather than on positions in the game tree. This is due to the LG formulation of final goals of players as certain target states of the state transition system.
|
|
|
LG-система функционирует, переходя из одного состояния в другое, т.е. ход игрока вызывает переход из текущего состояния LG-системы в другое состояние. Если последовательность состояний при переходах не имеет цикла, то эта последовательность определяет уникальный вариант (розыгрыш) на ДИ. Если последовательность состояний при переходах повторяется (циклит), то мы получим много розыгрышей, соответствующих одной последовательности переходов. Эти розыгрыши отличаются только тем, сколько раз они повторяют ходы, соответствующие одному периоду (циклу) последовательности состояний. Другими словами, розыгрыши отличаются лишь тем, по сколько раз они повторяют цикл. Важный факт состоит в том, что последовательности переходов в LG-системе образуют граф, а не дерево. Однако, важнейшие решения о том, закончена ли игра, и кто выиграл, основаны на состояниях LG-системы, а не на позициях ДИ. Это происходит из-за того, что в LG формулировки заключительных целей игроков основаны на описании целевых состояний LG-системы.
|
|
|
It is important to keep in mind the distinction between the two cases of using an LG algorithm to affect the evolution of an LG system. One case is when LG strategy for a player is applied against an LG strategy for the other player. The other case is when the source of moves of the other player is not an LG strategy. In all cases the LG strategy is represented by the same LG algorithm, where the player, for which a move is sought, is an input parameter of the algorithm.
|
|
|
Важно различать два случая использования LG-алгоритма, касающиеся развития LG-системы. Один случай, когда LG-стратегия одного игрока применена против LG-стратегии другого игрока. Другой случай, когда противник делает ходы не по LG-стратегии. Во всех случаях LG-стратегия представлена тем же самым LG-алгоритмом, в котором игрок, ход которого ищется, является входным параметром алгоритма.
|
|
|
Another important distinction is between moves in plays and moves in play variants or virtual plays or, simply, variants. The moves in a play constitute a sequence of moves that were actually made by players in the game. The moves in play variants are sequences of moves of both players that an LG strategy constructs in order to compute the move for the player. Such sequences of moves are possible continuations of the existing play, and they need not consist entirely or substantially of moves actually made by players.
|
|
|
Другое важное различие имеется между ходами в игре и ходами в вариантах игры (или в виртуальных розыгрышах или, просто, в вариантах). Ходы в игре - это последовательность ходов, которые были фактически сделаны игроками в процессе игры. Ходы в вариантах - это последовательности ходов (обоих игроков), которые строятся LG-стратегией, чтобы вычислить очередной ход игрока. Такие последовательности ходов - это возможные продолжения уже начавшейся партии (розыгрыша) и они вовсе не должны состоять (полностью или в значительной степени) из ходов, уже фактически сделанных игроками.
|
|
|
LG strategy has to rebuild the LG-search tree at each state for which it computes a move for the player. If LG strategy computes a move for the player at a state S1 and the next move at a state S2, both states will share many of the same structural components, because they are separated just by two moves: the move of the player and the move of the opponent. Thus, the LG algorithm tries to build LG-search tree for S2 by transforming that for S1.
|
|
|
LG-стратегия должна заново построить LG-дерево в каждом состоянии, для которого вычисляется ход игрока. Если LG-стратегия вычисляет ход для игрока в состоянии S1, а следующий ход противника ведёт в состояние S2, то оба состояния будут содержать много общих структурных компонентов, потому что они отделены только двумя ходами: ход игрока и ответный ход противника, если мы рассматриваем последовательные игры. Для параллельных игр эти состояния разделены одним (параллельным) ходом. Таким образом, LG-алгоритм пытается построить LG-дерево для состояния S2, преобразовывая его из LG-дерева для состояния S1.
|
|
|
One may think that the LG strategy computes a move for a player at a system’s state S, by constructing a subset of the state transition system graph for the LG system. In fact, LG algorithm uses information about the order of moves in an essential way. The graph above represents all play variants constructed by the LG algorithm in order to select a move for the player.
|
|
|
Можно считать, что LG-стратегия вычисляет ход для игрока, находящегося в состоянии S системы, построением подмножества графа всех переходов из одного состояния LG-системы в другое. Фактически, LG-алгоритм существенным образом использует информацию о порядке ходов. Вышеупомянутый граф, представляет все варианты, построенные LG-алгоритмом, при выборе очередного хода для игрока.
|
|
|
In reality, the LG algorithm produces an enumeration of a subset of this graph capturing the order of moves in all variants. Such an enumeration induces a subtree of the game tree extended as far as the variants went when they were computed by the LG algorithm. The subtree corresponds to playing the game beginning from the state S. Though, it is usually a very "narrow" finite subtree of the game tree corresponding to playing from S. There is one-to-one correspondence between the subtree of moves capturing all the LG variants on one hand, and the enumeration of a subset of the state transition graph according to the moves in all LG variants, on the other hand.
|
|
|
В действительности, LG-алгоритм генерирует перечисление подмножеств этого графа, тем самым, фиксируя порядок ходов во всех вариантах. Это перечисление порождает поддерево ДИ, которое простирается настолько, насколько продолжаются варианты, вычисленные LG-алгоритмом. Поддерево соответствует розыгрышам игры, начинающимся в состоянии S. Обычно, LG-дерево - это "очень узкое и глубокое" конечное поддерево полного ДИ, которое соответствует розыгрышам игры, начиная из состояния S. Существует взаимно однозначное соответствие между поддеревом ходов, охватывающим все LG-варианты, с одной стороны, и перечислением подмножеств графа переходов LG-системы, соответствующих ходам во всех LG-вариантах, с другой стороны.
|
|
|
The software system that applies LG maintains the play in the game and the game subtree representing all LG variants for the last state of the play. The LG algorithm also maintains the extensive structures (Section 1.5) associated with states that constrain the set of variants that LG computes.
|
|
|
Программная система, реализующая LG, поддерживает уже разыгранный вариант игры и его возможные продолжения - поддерево игры, которое представляет все найденные LG-варианты для последнего состояния игры (текущей позиции). LG-алгоритм также поддерживает обширные структуры данных (разд.1.5), связанные с состояниями и предназначенные для сокращения множества вычисляемых вариантов.
|
|
|
|
|
1.6 LG: Three Stages of Development
|
|
1.6 Три этапа развития LG
|
|
|
As in physics in the 17th century, in AI and, particularly, in LG, the major generalizations and break-through are still forthcoming. However, it is quite possible that the first signs of them are around us. In this respect, it would be helpful to look back at the history of development of LG. This history may be divided into three stages.
|
|
|
Также как в физике 17-го столетия, в области ИИ и, в частности в LG, важнейшие обобщения и крупнейшие достижения всё ещё впереди. Однако, весьма возможно, что их первые признаки уже рядом с нами. В этом отношении, было бы полезно оглянуться назад, обратившись к истории развития LG. Эта история может быть разделена на три этапа.
|
|
|
In the late 50s, in Moscow, Professor Mikhail Botvinnik, the World Chess Champion, began his investigation of the methodology of the most advanced chess players. Ten years later, this investigation resulted in the revolutionary ideas for the construction of chess programs that simulate grandmasters in playing chess. In the beginning of the 70s, Dr. Botvinnik initiated and directed research project PIONEER, with the author as key investigator. This research was conducted in Moscow at the National Research Institute for Electrical Engineering. It was funded by the USSR State Department of Science and Technology and the USSR Department of Energy. The goal of this research was to learn and implement as computer programs the methodology of the most advanced chess players as well as other domain experts for solving search problems almost without search, and, apply this approach to a wide spectrum of complex practical problems. A collection of powerful algorithms was developed within the project PIONEER (Botvinnik, 1984). Numerous experiments were performed to compare the systems based on that initial model and systems utilizing other approaches. The experiments showed that many problems, which were not solvable by the other approaches at all, were successfully solved by the prototypes of LG systems. Moreover, for the rest of the problems, the new systems were significantly faster than the other approaches. Project PIONEER continued through the end of 80s. The time period of 1958-1988 with preliminary design and vast experiments within project PIONEER is considered as the first stage of the development of LG (Section 1.7).
|
|
|
В конце 50-х годов в Москве Михаил Ботвинник, доктор электротехники и чемпион мира по шахматам, начал проводить научные исследования методологии лучших шахматистов. Десять лет спустя, эти исследования привели к революционным идеям в построении шахматных программ, которые моделируют игру гроссмейстеров. В начале 70-х, доктор Ботвинник организовал и возглавил исследования по проекту ПИОНЕР с автором этой книги, как ключевым разработчиком. Эти исследования проводились в Москве во Всесоюзном Научно-Исследовательском Институте Электроэнергетики (ВНИИЭ). Они финансировались ГКНТ СССР и Министерством Энергетики СССР. Цель исследования состояла в том, чтобы изучить и реализовать в виде компьютерных программ методологию лучших шахматистов, а так же экспертов в других областях, в решении переборных задач почти без перебора, и применить этот подход к широкому спектру сложных практических задач. Ряд эффективных алгоритмов был разработан в рамках проекта ПИОНЕР (Ботвинник, 1979, 1984). Были проведены многочисленные эксперименты для сравнения систем, основанных на начальной модели (ПИОНЕР) с системами, использующими другие подходы. Эксперименты показали, что многие из задач, которые были вовсе не разрешимы при других подходах, успешно решались прототипами будущих LG-систем. Кроме того, на тех задачах (где сравнение было возможно), новые системы работали значительно быстрее, чем системы при других подходах. Проект ПИОНЕР продолжался до конца 80-х годов. Период времени 1958-1988 годов, заполненный предварительными разработками и обширными экспериментами в рамках проекта ПИОНЕР, можно рассматривать как первый этап развития LG (разд.1.7).
|
|
|
Multiple attempts to formalize and, possibly, generalize the heuristics discovered in the course of the project PIONEER encountered enormous difficulties. These attempts began in the mid-70s pushed by the scientists who wanted other problem domains to benefit from the discoveries of this project. Another goal was to understand the fundamental nature of the results, to apply formal approach and theoretically evaluate the soundness, the completeness, and the running time of the developed algorithms. The difficulties were related to the unusual nature of the heuristic model being constructed. In particular, mathematical tools to be applied for formalization should have reflected the hierarchical and dynamic structure of the model, high flexibility of the subsystems, should have allowed global efficient control of every subsystem and the entire hierarchy. The development of the Hierarchy of Formal Languages, a mathematical model of heuristic algorithms of the project PIONEER, by the author is considered as the second stage of the LG heritage (Section 1.8). Time-wise, the first results were obtained in 1979, but the development continued through 1990 in Moscow at the National Research Institute for Electrical Engineering and later at the National Research Institute for Oil Development. This research was funded within the framework of the project PIONEER and through other sources.
|
|
|
Многократные попытки формализовать и, по возможности, обобщить эвристики, обнаруженные в ходе проекта ПИОНЕР, столкнулись с огромными трудностями. Эти попытки, начавшиеся в середине 70-х годов, были вызваны настоятельными требованиями многих учёных, которые хотели, чтобы результаты этого проекта оказались применимы в других проблемных областях. Другая цель состояла в том, чтобы понять фундаментальную природу результатов, применить формальный подход и теоретически оценить качество, полноту и вычислительную сложность алгоритмов, разрабатываемых в ходе проекта ПИОНЕР. Трудности были связаны с необычной природой эвристик, присущих построенной модели. В частности, математические средства, которые следовало применить для формализации, должны были отразить иерархическую и динамическую структуру модели, существенную гибкость подсистем, должны были допускать глобальное и эффективное управление как отдельно взятой подсистемой, так и всей иерархией подсистем. Разработку Иерархии Формальных Языков, как основу математической модели эвристических алгоритмов проекта ПИОНЕР, выполненную автором этой книги, можно рассматривать как второй этап истории развития LG (разд.1.8). Первые результаты были получены в 1979 году, но разработка продолжалась вплоть до 1990 года в Москве во ВНИИЭ, а позже во Всесоюзном Научно-Исследовательском Геологоразведочном Нефтяном Институте (ВНИГНИ). Эти исследования финансировались в рамках проекта ПИОНЕР и из других источников.
|
|
|
The year of 1990 is the beginning of the third stage of the development (Section 1.9) when LG was established as a self-determined field of research in Artificial Intelligence. This stage began at McGill University, Montreal, Canada. From September of 1991 to date, it continues at the University of Colorado at Denver, USA. In the 90s, the initial mathematical model was unified and generalized (Stilman, 1992-1998). Since both, the formal languages and the geometry of the operational district and subsystems, were involved, the advanced new model was named Linguistic Geometry in 1991. In retrospect, the previously developed part of this approach (stages one and two) is now being referred to as LG as well. The goals being pursued include the development of solid theoretical foundations, expansion to new problem domains, evaluation of complexity of classes of problems employing the LG tools and accuracy of these tools, development of efficient applications and a universal LG Testbed to be applied to a variety of problem domains.
|
|
|
1990-й год - это начало третьего этапа развития (разд.1.9), когда LG определилась как самостоятельная область исследований в ИИ. Этот этап начался в Мак-Гилльском Университете, в Монреале, Канада. С сентября 1991 года и до настоящего времени, он продолжается в Университете Колорадо в Денвере, США. В 90-х годах, предварительная математическая модель была унифицирована и обобщена (Штильман, 1992-1998). Поскольку формальная лингвистика и геометрия операционной области и подсистем, были использованы совместно, новая перспективная модель была названа Лингвистической Геометрией (LG) в 1991 году. Ретроспективно, мы будем использовать название LG при ссылках на предварительные исследования и результаты (этапы 1-й и 2-й). Цели исследований на 3-м этапе включали разработку прочного теоретического фундамента, оценку вычислительной сложности классов задач, допускающих LG-подход, оценку точности решений, получаемых при использовании LG-инструментов, расширение применимости LG к новым проблемным областям для разработки эффективных LG-приложений, а также создание программного прототипа универсального LG-testbed (испытательного стенда) - среды для разработки и отладки приложений LG в разнообразных проблемных областях.
|
|
|
What was not expected or planned in advance is the re-development of the top-level of LG, the Language of Translations, employing the so-called no-search approach. The ability to generate provably optimal solutions for classes of problems without any tree-based search shows the fascinating power of LG that originated from expert heuristics. This investigation allowed us to identify a new class problems of low (polynomial) computational complexity among the problems that were considered computationally hard (exponential or worse). During the third stage, the funding was provided by a number of sources, including the National Science and Engineering Research Counsel (NSERC) of Canada and McGill University, Montreal, Canada, University of Colorado at Denver, USA, the U.S. Air Force Office of Scientific Research, and the U.S. Department of Energy through Sandia National Laboratories, Albuquerque, NM.
|
|
|
Что не ожидалось и не планировалось заранее, так это перестройка верхнего уровня LG - Языка Переводов - при использовании так называемого беспереборного подхода. Способность генерировать доказуемо оптимальные решения для классов Рети-подобных задач вообще без перебора ходов, т.е. без какого-либо перебора на дереве, демонстрирует удивительную мощь LG, которая родилась из экспертных эвристик. Проведенные исследования позволили идентифицировать новый класс задач низкой (полиномиальной) вычислительной сложности среди задач, которые считались в вычислительном отношении трудными (экспоненциальными или хуже). В течение третьего этапа финансирование было обеспечено из многих источников, включая Национальный Научно-Исследовательский Совет (NSERC) Канады и Мак-Гилльский Университет в Монреале, Офис Научных Исследований ВВС США (AFOSR), Университет Колорадо в Денвере, США, Министерство Энергетики США через Сандийскую Национальную Лабораторию в Альбукерке.
|
|
|
It is likely that several important events taking place in 1999, including publication of this book and a substantial grant from DARPA, will assist in advancing the theory and building real world applications of LG, and manifest the beginning of a new fourth stage of the development of LG.
|
|
|
Вероятно, несколько важных событий, имевших место в 1999 году, включая публикацию этой книги и значительный грант от Агентства Перспективных Исследований Министерства Обороны США, помогут в развитии теории и разработке программных приложений LG для решения задач из реальной жизни. Возможно, эти события знаменуют начало нового четвертого этапа в развитии LG.
|
|
|
|
|
1.7 Stage One: Project PIONEER
|
|
1.7 Этап 1: проект ПИОНЕР
|
|
|
The first ten years of research, since 1958, resulted in publication of the book "Algorithm for Playing Chess" (Botvinnik, 1968, 1970). While the mathematical formalization of the algorithm published in the book may be somewhat questionable, the major principles for search reduction laid a solid foundation for further development. Another publication entitled "A Flow-Chart of the Algorithm for Playing Chess" (Botvinnik, 1972) should be considered as an official start of the project PIONEER. Unfortunately, the above publications included nothing beyond ideas and low level flow charts. The algorithm and the program were yet to be developed.
|
|
|
Первые десять лет исследований, начиная с 1958 года, закончились публикацией книги "Алгоритм игры в Шахматы" (Ботвинник, 1968, 1970). В то время как математическое описание алгоритма было ещё недостаточным для программирования (и, возможно, несколько сомнительным), основные принципы сокращения перебора заложили прочный фундамент для дальнейшего развития. Другая публикация "Блок-схема Алгоритма игры в Шахматы" (Ботвинник, 1972) уже может рассматриваться как официальное начало проекта ПИОНЕР. К сожалению, обе вышеупомянутые публикации не включали ничего кроме идей и набора блок-схем для низкоуровневых процедур алгоритма. Собственно алгоритм и программу шахматный игры ещё только предстояло разработать.
|
|
|
The research team involved in this project had two subjects for investigation: advanced experts (like Botvinnik himself) and computer programs, once they were developed. These programs included computer chess program PIONEER 1.x and a number of programs PIONEER 2.x - 4.x for planning and scheduling. Feedback from both resulted in constant rethinking and multiple redevelopment of both algorithms and programs. Many old and new ideas were tested in the course of the project. For example, the idea of trajectories limited by a horizon and the idea of decomposition of a complex system into the dynamic hierarchy of subsystems, proved to be essential from the very beginning. That was not the case with the second-level subsystem, the network of trajectories. Defined originally as the key area of a combat, later as a zone (in multiple versions), and as a chain of trajectories, this subsystem went through a number of major and minor changes. Heuristic algorithms for generation of the first and second-level subsystems, trajectories and Zones, were presented in (Stilman, 1975, 1977, 1979, 1984a). Similar problems were encountered with the higher-level subsystems and with the algorithm for global control later formalized as Grammar of Translations.
|
|
|
Группа исследователей, занятых в этом проекте, имела два предмета научных исследований: выдающихся экспертов (подобно самому Ботвиннику) и компьютерные программы (после того как они были разработаны). Эти программы включали шахматную программу ПИОНЕР 1.x и множество программ ПИОНЕР 2.x - 4.x для планирования народного хозяйства СССР и составления графика ремонтов. Взаимосвязи между этими предметами исследований приводили к постоянному пересмотру наших взглядов и к многократной перестройке алгоритмов и программ. Много старых и новых идей были проверены в ходе проекта ПИОНЕР. Например, идея Траекторий, ограниченных горизонтом, и идея о декомпозиции Сложной Системы в динамическую иерархию подсистем доказали свою важность с самого начала. Этого не произошло с подсистемой второго уровня - Сетью Траекторий. Определенная первоначально, как ключевая область боя, а позже как Зона (в многочисленных версиях) и как Цепочка фигур, эта подсистема прошла множество существенных и менее значительных изменений. Эвристические алгоритмы для генерации подсистем первого и второго уровня - Траекторий и Зон - были представлены в (Штильман, 1975, 1977, 1984a). Подобные проблемы возникали и с подсистемами высокого уровня, и с алгоритмом глобального управления, позже формализованным как Грамматика Переводов.
|
|
|
By the end of 1976, the first version of the chess program PIONEER was completed. It was tested on solving chess endgames. Of course, the goal was not just to solve endgames. The solutions should have been obtained employing the search trees close to the trees of variants analyzed by a chess expert. With respect to accuracy, the generated solutions had never been considered as the absolute optimal solutions of the problems. Moreover, for a vast majority of the endgames, optimal solutions are still unknown. A proof of optimality employing conventional search algorithms requires enormous search and, usually, is beyond capabilities of any computers (Section 1.2). What is usually called a solution is a variant (or several variants) which experts agreed upon. A deeper understanding of optimality and its role in LG came much later in the third stage of the LG development (Section 1.9 and Chapter 13).
|
|
|
К концу 1976 года первая версия шахматной программы ПИОНЕР был закончена. Она была проверена на решении шахматных этюдов. Конечно, цель состояла не только в том, чтобы решить эти этюды. При решении нужно было получить дерево перебора, близкое к тому, которое строит шахматный мастер. Что касается точности, то получаемые решения никогда не рассматривались как оптимальные. Кроме того, для огромного большинства этюдов оптимальные решения до сих пор неизвестны. Доказательство оптимальности при использовании традиционных алгоритмов типа «брут форс» требует огромного перебора, который часто превышает возможности любых компьютеров (разд.1.2). То, что обычно называют решением - это вариант (или несколько вариантов), которые признаны экспертами. Более глубокое понимание оптимальности и его роли в LG пришло намного позже на 3-м этапе развития LG (разд.1.9 и глава 13).
|
|
|
The first two endgames selected for the program tests,
R.Reti
and
M.Botvinnik-S.Kaminer endgames, are considered simple for a chess player. However, this simplicity is hidden behind million-move search trees to be analyzed employing the brute force approach. Of course, a chess expert is able to avoid this multitude of computations. During the experiments with PIONEER, a number of parameters evaluated included the branching factor (Section 1.2) as well as some other parameters of the search (Botvinnik, 1979, 1984). The search tree generated by PIONEER in January of 1977 while solving the R.Reti endgame contained 54 moves (T=54). Hence, taking into account that the depth of the search required here, L=6, a branching factor
B≈1,68 was obtained (1.2.2). The search trees generated by conventional chess programs for this endgame include about 106 moves. In the M.Botvinnik and S.Kaminer endgame (Botvinnik, 1979, 1984), the total number of moves included in the search was equal to 145, maximum length L=12, and
B≈1,35. Although both endgames are solvable by conventional chess programs, these results were very interesting because of substantial reduction of the branching factor. One of these problems, the R.Reti endgame, serves as a model for the far reaching generalizations in LG (Chapters 3, 4, 6, 13, and 14).
|
|
|
Первые два этюда, отобранные для тестирования программы ПИОНЕР - этюд
Рети
и этюд
М.Ботвинника-С.Каминера, считаются простыми для шахматиста. Однако эта простота скрыта за миллионами ходов в дереве перебора, которые должны быть проанализированы при поиске решения по методу «брут форс». Конечно, шахматный эксперт способен избежать этого множества вычислений. Во время экспериментов с ПИОНЕРом оценивалось множество параметров, включая коэффициент ветвления (разд.1.2), а также некоторые другие параметры перебора (Ботвинник, 1979, 1984). Дерево перебора, построенное ПИОНЕРом в январе 1977 года при решении этюда Рети, содержало 54 хода (T=54). Следовательно, принимая во внимание, что глубина перебора, необходимого для решения этой задачи должна быть не меньше L=6, мы получили коэффициент ветвления
B≈1,68 (1.2.2). Деревья перебора, построенные традиционными шахматными программами для этого этюда, включают приблизительно 106 ходов. В этюде Ботвинника и Каминера (Ботвинник, 1979, 1984), общее количество ходов, включённых в перебор, было равно 145, максимальная глубина L=12 и
B≈1,35. Хотя оба этюда могут быть решены традиционными шахматными программами, эти результаты были очень интересны из-за существенного уменьшения коэффициента ветвления. Одна из этих задач, этюд Рети, продолжает служить моделью для далеко идущих обобщений в LG (главы 3, 4, 6, 13 и 14).
|
|
|
Among the variety of complex problems solved by PIONEER, we will discuss two more. Both have yet to be solved by the conventional chess programs. The search algorithms with alpha-beta pruning (Section 1.2) failed to provide a substantial reduction of the branching factor. As a result, the expected run times were not feasible.
|
|
|
Среди разнообразных сложных задач, решённых ПИОНЕРом, мы обсудим ещё две. Обе задачи до сих пор не могут быть решены традиционными шахматными программами. Алгоритмы перебора с альфа-бета отсечением (разд.1.2) не в состоянии обеспечить существенное уменьшение коэффициента ветвления. Поэтому время, требуемое для расчёта, оказывается немыслимым.
|
|
|
The first problem is the
G.Nadareishvili endgame (Nadareishvili,
1975,
1976; Botvinnik,
1979,
1984). It was solved by PIONEER in August of 1977. The total number of nodes generated was T=200, while the depth of the search required to find a solution is equal to 25. Consequently,
B≈1,14. The unreduced branching factor might be estimated as
B≈15. The solution of this endgame demonstrated power of the heuristic model, the foundation of PIONEER. A dynamic hierarchy of subsystems, trajectories and networks, allowed us to find a very deep solution almost without branching. Of course, this was just a solution approved by experts. At that time nobody raised the question of optimality or even about the accuracy of this solution. Now, 20 years later, we can suggest that this is the mathematical optimum. It is reasonable to expect that this will be proved employing ideas of the no-search approach in LG (Chapter 13) in the near future. The G.Nadareishvili endgame also served as a pattern for a number of generalizations included in this book (Chapter 5).
|
|
|
Первая задача - этюд
Г.Надареишвили (Надареишвили,
1976; Ботвинник,
1979,
1984). Он был решён ПИОНЕРом в августе 1977 года. Общее количество построенных узлов было T=200, в то время как глубина перебора, требуемого для нахождения решения L=25. Следовательно,
B≈1,14. Неуменьшенный коэффициент ветвления для алгоритмов типа «брут форс» здесь можно оценить как
B≈15. Решение этого этюда продемонстрировало мощь эвристической модели, на которой основан ПИОНЕР. Динамическая иерархия подсистем, Траекторий и Сетей, позволила нам найти очень глубокое решение почти без ветвления. Конечно, это было всего лишь решение, одобренное экспертами. Тогда никто не поднимал вопроса об оптимальности или хотя бы о точности этого решения. Теперь, 20 лет спустя, мы можем предположить, что это - математический оптимум. Разумно ожидать, что это будет доказано при использовании идей беспереборного подхода в LG (глава 13) в ближайшем будущем. Этюд Надареишвили также послужил образцом для множества обобщений, включенных в эту книгу (глава 5).
|
|
|
The second complex problem is the middle-game position in the legendary game played by World Chess Champions
M.Botvinnik and H.-R.Capablanca in 1938. This chess combination is usually considered as an eternal example of brilliant chess art. The start position contains 19 pieces and the unreduced branching factor might be estimated as
B≈20. The depth of the search should not be less than 23. In April of 1980, program PIONEER generated a search tree of 40 nodes with the branching factor
B≈1,05 (Botvinnik, 1980a, 1980b, 1982). A solution found by PIONEER was exactly the same as the variant played by the champions in 1938. It is likely that this solution is provably optimal.
|
|
|
Вторая сложная задача - это позиция в середине игры из легендарной партии
М.Ботвинник и Х.-Р.Капабланка, сыгранной в 1938 году на АВРО-турнире (Голландия)(Ботвинник, 1984a). Эту шахматную комбинацию обычно рассматривают как бессмертный пример выдающегося шахматного мастерства. Начальная позиция содержит 19 фигур, а неуменьшенный коэффициент ветвления можно оценить как
B≈20. Глубина перебора для этой задачи не должна быть меньше, чем 23. В апреле 1980 года программа ПИОНЕР построила дерево перебора из 40 узлов с коэффициентом ветвления
B≈1,05 (Ботвинник, 1980a, 1980b, 1982, 1987). Решение, найденное ПИОНЕРом, было точно таким же, как и вариант в той партии 1938 года. Вероятно, это решение является доказуемо оптимальным.
|
|
|
In 1981-1988, all the R&D on project PIONEER were supported by the software development environment called PROGRAMMER’S WORKBENCH (PW), (Stilman, 1994f). It was developed by Mirniy, Roizner, Chudakov, and Stilman (1986), and later significantly expanded by Mirniy, Chudakov, and Stilman (1988). PW was intended to support concurrent software development and configuration maintenance of large-scale research projects. PIONEER and other complex projects included an extended prototype period. Basically, the programs were used as tools for the investigation and redevelopment of algorithms. The entire software life cycle was considered as a sequence of prototypes. Each prototype should have been extremely flexible to provide multiple redesigns. PW supported multiple redevelopment iterations of changeable prototypes through the universal hard skeleton of software versions. Additionally, PW effectively supported teamwork on project PIONEER by combining independence of a software designer acting alone and strict discipline of cooperative research projects. While Dijkstra (Dijkstra, 1976; Gries, 1983; Stilman, 1994f) was the source language fully supported by PW, the actual development (including the debug mode) was conducted employing the highest-level problem-oriented language. PW allowed us to construct, expand, and maintain various versions of this language for different problem domains. PW was implemented for IBM mainframe hardware. Later, the PW tools were used at several research institutions for the development and maintenance of large-scale Artificial Intelligence projects. These tools were ready for expansion to support object-oriented frameworks.
|
|
|
В 1981-1988 годах, все исследования и программные разработки по проекту ПИОНЕР проводились при помощи системы поддержки разработки программ, называвшейся РАБОЧИМ МЕСТОМ ПРОГРАММИСТА (PROGRAMMER'S WORKBENCH - PW), (Штильман, 1994f). Система PW была разработана Мирным, Ройзнером, Чудаковым и Штильманом (1986), и позже переработана и расширена Мирным, Чудаковым и Штильманом (1988). PW была предназначена для того, чтобы поддержать параллельную разработку и конфигурацию программного обеспечения (ПО) для крупномасштабных научно-исследовательских работ. ПИОНЕР и другие сложные проекты включали расширенный период опытной эксплуатации образцов (прототипов) ПО. В основном, компьютерные программы использовались как инструменты для научных исследований и перестройки сложных алгоритмов. Полный цикл жизни компьютерных программ рассматривался как последовательность прототипов. Каждый прототип должен был быть чрезвычайно гибким, чтобы обеспечить многократное перепроектирование. PW поддерживала многократные итерации при перестройке изменяющихся прототипов благодаря жесткому универсальному каркасу версий ПО. Дополнительно, PW эффективно автоматически поддерживала взаимодействие разработчиков в проекте ПИОНЕР, обеспечивая независимость проектировщиков PW от остальных сотрудников (пользователей PW) и одновременно поддерживая строгую дисциплину коллективных разработок. Хотя язык Dijkstra (Дейкстра, 1976; Грис, 1983; Штильман, 1994f) был входным языком (транслятора), полностью реализованным в PW, фактическая разработка (включая отладку) проводилась с использованием проблемно-ориентированного (на LG) языка очень высокого уровня. PW позволила нам создавать, расширять и поддерживать различные версии этого языка и для других проблемных областей. PW была реализована на IBM 370/144 - оригинальном американском компьютере, на котором в эти годы и велась разработка ПИОНЕРа. Позже, PW инструменты использовались в нескольких НИИ на советских ЭВМ для разработки и поддержки крупномасштабных проектов в области Искусственного Интеллекта. Инструменты PW были подготовлены к модернизации для поддержки объектно-ориентированного программирования.
|
|
|
Project PIONEER resulted in the development of one of the most interesting and powerful heuristic models based on heuristic networks. Application of the developed model to the chess domain was implemented in full as program PIONEER 1.x (Botvinnik, 1979, 1982, 1984, 1989). A similar heuristic model was implemented for the long-range planning and scheduling in a number of computer programs PIONEER 2.x, 3.x, 4.x. They were used for scheduling of maintenance of power units, for smoothing the graph of power consumption, and for planning the national economy in the former USSR (Stilman, 1985a, 1993a). The models were introduced in (Stilman, 1976c, 1977, 1979, 1994a; Botvinnik, 1970, 1972, 1975, 1979, 1982, 1984, 1987, 1989), (Reznitskiy and Stilman, 1983 ; Reznitskiy, Bordiugov and Stilman, 1983), (Botvinnik et al., 1983; Botvinnik, 1989), (Stilman, 1978, 1985b, 1985c, 1993d) in the form of ideas, plausible discussions, and program implementations.
|
|
|
Проект ПИОНЕР закончился разработкой одной из самых интересных и мощных эвристических моделей, основанной на эвристических сетях. Применение разработанной модели к шахматной игре было полностью реализовано в виде программы ПИОНЕР 1.x (Ботвинник, 1979, 1982, 1984, 1987, 1989). Аналогичная эвристическая модель была также реализована для долгосрочного календарного планирования в виде набора программ ПИОНЕР 2.x, 3.x, 4.x. Они использовались для составления графика ремонтов электроагрегатов, для сглаживания графика потребления мощности и для планирования народного хозяйства в прежнем СССР (Штильман, 1985a, 1993a). Эти модели (Штильман, 1976c, 1977, 1979, 1994a; Ботвинник, 1968, 1972, 1975, 1979, 1989), (Резницкий и Штильман, 1983; Резницкий, Бордюгов и Штильман, 1983), (Ботвинник и др., 1983; Ботвинник, 1989), (Штильман, 1978, 1985b, 1985c, 1993d) были представлены в форме идей, правдоподобных рассуждений и работающих программ.
|
|
|
Experiments with maintenance scheduling programs PIONEER 2.x demonstrated the advantages of the new approach. The program PIONEER 2.1 for monthly scheduling of power units generated various schedules with a reduced branching factor not exceeding 1,06, down from 50-100 for the brute force approach (Reznitskiy and Stilman, 1983), (Stilman, 1985a). Experiments with program PIONEER 2.2 for annual (365 days) maintenance scheduling of power equipment also demonstrated a reduced branching factor close to 1. In contrast with PIONEER 2.1, this program was able to maximize the number of power units included on the schedule by adjusting the duration of maintenance of these units. A new level of benefits was shown by the program PIONEER 2.3 that generated annual power maintenance schedules by adjusting the values of the power reserve. Slight adjustments of the power reserve (within the range of 6%) allowed this program to schedule maintenance of all the power plants that submitted requests. The most interesting results in scheduling were achieved by program PIONEER 2.4 for annual scheduling with multiple resource allocation including various types of maintenance personnel. These requirements resulted in a significant growth of the unreduced branching factor while the program managed to reduce it down to 1,005. It generated high quality annual schedules for the USSR National Power System. Application of LG to scheduling and additional details about scheduling programs are presented in Chapter 7.
|
|
|
Эксперименты с программами составления графика ремонтов ПИОНЕР 2.x продемонстрировали преимущества нового подхода. Программа ПИОНЕР 2.1 для составления месячного графика ремонтов электроагрегатов генерировала различные графики с коэффициентом ветвления, не превышающим 1,06, что составляло 50..100-кратное уменьшение этого коэффициента по сравнению с методом «брут форс» (Резницкий и Штильман, 1983; Штильман, 1985a). Эксперименты с программой ПИОНЕР 2.2 по составлению годового (на период в 365 дней) графика ремонтов электроагрегатов также продемонстрировали уменьшение коэффициента ветвления до величины близкой к 1. В отличие от ПИОНЕРа 2.1, эта программа была способна максимизировать число электроагрегатов, включённых в график ремонтов, регулируя продолжительность ремонта этих агрегатов. Особые качества были продемонстрированы программой ПИОНЕР 2.3, которая генерировала годовые графики ремонта агрегатов, регулируя значения резерва мощности. Небольшие вариации резерва мощности (в пределах диапазона 6%) позволяли этой программе включать в план ремонта все электростанции, которые подали заявки. Самые интересные результаты в составлении графика ремонтов были получены программой ПИОНЕР 2.4 для составления годового графика с распределением многочисленных ресурсов, включая различные типы ремонтного персонала. Такая постановка задачи приводила к существенному росту коэффициента ветвления; программа сумела уменьшить этот коэффициент до 1,005. Это позволило генерировать высококачественные годовые графики ремонтов для Единой Энергосистемы бывшего СССР. Применение LG к календарному планированию и дополнительная информация о программах составления графиков ремонта представлены в главе 7.
|
|
|
Programs PIONEER 3.1 and 3.2 allowed to smooth the weekly graphs of power consumption by changing weekly schedules (moving off days) for various consumers. They decreased the maximums of power consumption by 3.5% while minimizing the number of changed schedules (Botvinnik and Mirniy, 1983).
|
|
|
Программы ПИОНЕР 3.1 и 3.2 позволяли сглаживать еженедельные графики потребления мощности, сдвигая выходные дни для различных потребителей. Они уменьшили максимумы потребления мощности на 3,5% при уменьшении числа потребителей со сдвинутыми выходными (Ботвинник и Мирный, 1983).
|
|
|
The top achievement in applying PIONEER’s model in the non-chess domains was the development of the programs PIONEER 4.1 and 4.2 for planning the USSR national economy for 15 and 25 years, respectively. These programs balanced the production of the national industry and the national budget based on the aggregated 18-branch model of the national economy (Reznitskiy, 1987).
|
|
|
Главным достижением модели ПИОНЕР в применении к не шахматным областям была разработка программ ПИОНЕР 4.1 и 4.2 для планирования народного хозяйства СССР на периоды в 15 и 25 лет соответственно. Эти программы балансировали продукцию государственной промышленности и бюджет, основываясь на агрегированной модели, включавшей 18 отраслей народного хозяйства (Резницкий, 1987; Ботвинник, 1989).
|
|
|
The results obtained within the framework of PIONEER in solving complex search problems for various problem domains indicate that implementations of the dynamic hierarchies resulted in the construction of highly goal-driven algorithms that generated search trees with the branching factor close to one.
|
|
|
Результаты, полученные в рамках проекта ПИОНЕР при решении сложных переборных задач для различных проблемных областей, показывают, что реализация динамических иерархий привела к построению в высшей степени целенаправленных алгоритмов, которые генерировали деревья перебора с показателем ветвления близким к 1.
|
|
|
What was in common in those hierarchies? What formal tools could be used to reflect these commonalties and to apply them in different problem domains?
|
|
|
Что было общего в этих иерархиях? Какие формальные средства могли бы быть использованы, чтобы отразить эту общность и применить её в других проблемных областях?
|
|
|
|
|
1.8 Stage Two: Mathematical Tools
|
|
1.8 Этап 2: Математические Инструменты
|
|
|
In 1979-1990, the first version of formal tools for LG was developed (Fig.1.5). A story behind this result is instructive. It was clear that the mathematical tools should have been discrete, symbolic, and should have reflected the dynamic hierarchy of subsystems. The specific requirements looked as follows.
|
|
|
В 1979-1990 годах была разработана первая версия формальных инструментов для LG (рис.1.5). История получения этих результатов - поучительна. Было ясно, что математические инструменты должны быть дискретными, символическими и должны отражать динамическую иерархию подсистем. Более точно эти требования описаны ниже.
|
|
|
The mathematical tools should reflect the problem statement as a system of local agents, the entities, and their locations. The entities are broken down in two sides with opposing interests. They can move by changing their locations. Some of the locations are free from entities but may be occupied later. A move takes place during one time interval. All time intervals are to be equal. Also, the entities should have well-defined rules limiting their movements. A system operation can be reflected as a variant of moves. Every variant can be compared with other possible variants. A solution of a problem is the operation selected from the rest according to a certain criterion of optimality. A typical difficulty of such selection is related to the number of possible variants and, consequently, to the running time of the search required. Quite often, for real world problems, these time increased to the levels that made them practically unsolvable.
|
|
|
Математические инструменты должны отражать постановку задачи как системы локальных агентов и их местоположений. Агенты разделяются на две стороны с противоположными интересами. Агенты могут перемещаться, изменяя свои местоположения - пункты. Некоторые из пунктов остаются свободными от агентов, но могут быть заняты ими позже. Ход делается в течение одного временного интервала. Все интервалы должны быть равны по времени. Также, агенты должны иметь чёткие правила, ограничивающие их движения. Функционирование системы можно представить как вариант, состоящий из последовательности ходов. Каждый вариант может сравниваться с другими возможными вариантами. Решение задачи - это вариант, выбранный среди всех по некоторому критерию оптимальности. Типичная трудность такого выбора связана с числом возможных вариантов и, следовательно, с продолжительностью требуемого перебора. Весьма часто, для задач из реальной жизни, время перебора возрастает так сильно, что они становятся практически неразрешимыми.
|
|
|
The formalization of the problem statement shown above was not of great concern. This class of problems could be formally represented employing numerous existing techniques, and all representations are equivalent. However, the chosen representation of the problem statement should be well coupled with the formal representation of the method used to solve it, the LG approach. It should serve as a foundation and a mathematical environment for the formal representation of the dynamic hierarchy of subsystems. A formal problem statement (Chapter 2) was developed by following the theories of formal problem solving and planning by McCarthy and Hayes (1969), Fikes and Nilsson (1971), Sacerdoti (1975), McCarthy (1980), Nilsson (1980), and others, based on the first order predicate calculus. The main idea of this formalization of the problem statement was borrowed from the system STRIPS developed by Fikes and Nilsson (1971).
|
|
|
Формализация постановки задачи в том виде, как она описана выше, не представляла трудности. Этот класс задач мог быть формально представлен с использованием многочисленных уже существующих методов, причём все они эквивалентны. Однако, важно, чтобы выбранное формальное представление постановки для класса задач соответствовало формальному представлению метода, который использовался при решении этих задач, т.е. LG-подходу. Это представление должно было стать основой и математической средой для формального представления динамической иерархии подсистем. Формальная постановка задачи (глава 2) была разработана, следуя известным теориям формального решения задач и планирования, разработанным в статьях (Мак-Карти и Хайеса, 1969; Файкса и Нильсона, 1971; Сакердоти, 1975; Мак-Карти, 1980; Нильсона, 1980 и в других), которые основаны на исчислении предикатов 1-го порядка. Основная идея этой формализации была заимствована из системы STRIPS, разработанной Файксом и Нильсоном (1971).
|
|

Figure 1.5 Origin of LG: formal tools and heuristics.
|
|
Рис.1.5 Происхождение LG: формальные инструменты и эвристики.
|
|
|
Even a brief description of requirements for representation of dynamic hierarchies given below shows that this task was incomparably more difficult than formalization of the problem statement. It took a number of years to come up with a satisfactory solution.
|
|
|
Даже краткое описание требований для представления динамических иерархий, приведенное ниже, показывает, что проблема формализации этого представления была несравнимо труднее, чем формализация самой постановки задачи. Прошли годы, прежде чем удовлетворительное решение было получено.
|
|
|
A hierarchy to be introduced is intended to reveal and make use of the inherent hierarchical relationship between entities and groups of entities with respect to the main goal of a system. The lower level of the hierarchy is a trajectory, a planning path, with an entity moving along it. When it moves forward, part of a trajectory that is left behind should disappear, and re-appear again, when an entity backtracks during the search to explore another path. Formal tools should have generated all kinds of trajectories encountered in a number of problem domains, e.g., a shortest path, a path going around obstacles, etc.
|
|
|
Иерархия, которую следовало ввести, должна была проявить и отразить ту глубокую иерархию взаимоотношений, которая возникает между агентами и группами агентов, при их стремлении к главной цели системы. Низший уровень иерархии - это Траектория, т.е. планируемый путь вместе с агентом, движущимся по этому пути. Когда агент продвигается, то пройденная часть траектории должна исчезнуть и вновь появиться при возврате агента в процессе перебора (когда агент "пятится"), чтобы исследовать другой путь. Формальные инструменты должны генерировать все виды траекторий для разных проблемных областей, например, самый короткий путь, путь для обхода препятствий и т.д.
|
|
|
The higher levels of the hierarchy are networks of trajectories (with their entities). Every network has its ultimate goal related to a specific location, the final destination. A number of types of networks were introduced: attack Zones, domination Zones, retreat Zones, etc. Every network includes entities participating in achieving the ultimate goal. This participation is twofold. Entities of one side pursue their goal by moving, protecting each other, and destroying the enemies. Entities of the other side, by similar actions, do their best to prevent the opponent from achieving the goal. An entity can participate in many networks simultaneously. The movements of entities are organized in a timely fashion. For example, if an entity has enough time to move along a trajectory to intercept an opposing entity, this trajectory is included in the network and the movement is allowed. If this is not the case, the trajectory is dropped. In a network, parts of trajectories and bundles of trajectories with their entities disappear when movement along them does not make sense with respect to the ultimate goal. This may be related to the timing, the state configuration, or other reasons. Calculations of time and other factors related to the network construction and re-construction are done within each network independently. For this purpose, the other networks are ignored. Networks can be connected to each other if the ultimate goal of one of them becomes the goal of the joint network, while the goals of the components become subordinate to the main goal.
|
|
|
Более высокие уровни иерархии - это Сети Траекторий (вместе с их агентами). Каждая Сеть Траекторий должна иметь конечную цель с определенным местоположением, т.е. конечным пунктом назначения. Множество сетей должно включать Зоны нападения, Зоны доминирования, Зоны отступления и т.д. Каждая сеть должна включать агентов, участвующих в достижении конечной цели. Это участие является двойным. Агенты одной стороны преследуют свою цель, перемещаясь, защищая друг друга и уничтожая врагов. Агенты другой стороны подобными же действиями стараются препятствовать противнику в достижении его цели. Агент может участвовать во многих сетях одновременно. Движения агентов организованы с учётом времени. Например, если агент имеет достаточно времени, чтобы пройти по траектории и перехватить агента противоположной стороны, то эта траектория включается в сеть и движение по ней разрешается. Если дело обстоит не так, то траектория отбрасывается. При перемещении агентов в другие пункты часть траекторий и пучков траекторий сети застывает, когда движение агентов по ним уже не имеет смысла относительно конечной цели. Это может быть связано с недостатком времени, конфигурацией состояния (позицией) или с другими причинами. Вычисление времени и других параметров, связанных с построением и реконструкцией сети, производится для каждой сети независимо друг от друга. Связи с другими сетями при этом игнорируются. Сети могут быть связаны друг с другом, если конечная цель одной из них становится главной целью объединенной сети, тогда цели других сетей-компонентов подчиняются главной цели.
|
|
|
In the 70s, a number of existing mathematical tools was evaluated and dropped. Usually, they did not explicitly reflect the hierarchy of subsystems or did not provide sufficient flexibility for representation of dynamic subsystems. For example, these deficiencies are inherent to the representation of trajectories and networks as graphs. At that point, a linguistic representation was considered as a candidate. Indeed, a trajectory is a finite sequence of planning steps of an entity while a string is a finite sequence of symbols. It seems reasonable to represent trajectories as formal strings of symbols. In this case, a set of trajectories could be represented as a formal language. The next question to be answered was how to represent the hierarchies via languages. It was quite a surprise when we realized that the linguistic representation of hierarchies is most natural. Indeed, a set of dynamic subsystems could be represented as a hierarchy of formal languages where each sentence, a group of words (a string of symbols), of the lower level language corresponds to a word in the higher level one. This is a routine procedure in our natural language. For example, the phrase: "A man who teaches students" introduces the hierarchy of languages. Symbols of the lower-level language may include all the English words except "professor". A higher-level language might be the same language with addition of one extra word "professor" which is simply a short designation for "A-man-who-teaches-students". Note that the hierarchical architecture of natural languages and related approaches adopted in LG are examples of the general semiotic mechanism of multiresolution introduced later by Meystel (1996a, 1996b).
|
|
|
В 70-х годах многие из известных математических инструментов были пересмотрены и отброшены. Обычно, они не отражали явно иерархию подсистем или не обеспечивали достаточную гибкость для представления их динамичности. Например, эти недостатки свойственны представлению траекторий и сетей в виде графов. В этой связи лингвистическое представление также рассматривалось в качестве кандидата. Действительно, траектория - это конечная последовательность запланированных ходов агента, в то время как слово - это конечная последовательность символов. Кажется, разумным представить траектории как формальные слова, составленные из символов. В этом случае множество траекторий можно представить как формальный язык. Но как с помощью языков представить иерархии? К нашему удивлению мы поняли, что лингвистическое представление иерархий является и наиболее естественным. Действительно, множество динамических подсистем можно представить как иерархию формальных языков, в которой каждое предложение - группа слов языка более низкого уровня - соответствует слову в высокоуровневом языке. Это стандартная процедура на нашем естественном языке. Например, фраза: "Человек, который преподаёт студентам", вводит иерархию языков. Символы языка низкого уровня могут включать все слова кроме слова "профессор". Высокоуровневый язык мог бы быть тем же самым языком, но дополненным ещё одним словом "профессор", которое является просто кратким обозначением для фразы "человек, который преподаёт студентам". Следует отметить, что иерархическая архитектура естественных языков и аналогичный подход, принятый в LG, - это примеры общего семиотического механизма мультирезолюций (иерархии моделей разного разрешения), введенного позже А.Майстелом (Майстел, 1996a, 1996b).
|
|
|
The key question remained: what are the specific languages to be used for the model? In the 50s through 70s, a formal syntactic approach to the investigation of properties of natural language resulted in the fast development of the theory of formal languages by Chomsky (1963), Ginsburg (1966), Hopcroft and Ullman (1979), and others. This development provided an interesting opportunity for dissemination of this approach to different areas. In particular, there came an idea of analogous linguistic representation of physical images (Fig.1.5). This idea was successfully developed into syntactic methods of pattern recognition by Narasimhan (1966), Fu (1974, 1982) and Pavlidis (1977), and picture description languages by Shaw (1969), Feder (1971) and Rosenfeld (1979). The Plex languages introduced by Feder (1971) demonstrated a particular descriptive power. In a usual string of symbols, every symbol is connected only with two neighbors, left and right. It has two attaching points. In Plex languages, a symbol called NAPE (an n Attaching-Point Entity) can have an arbitrary number n of attaching points for joining to other symbols. The resulting strings represent general higher-dimensional patterns that allow us to generate images that represent trees, sophisticated chemical formulas, electrical circuits, etc. Something similar could be done in LG with trajectories and networks.
|
|
|
Оставался ключевой вопрос о том, какие языки следует использовать для этой модели? В течение 50-70-х годов, формально-синтаксический подход к исследованию свойств естественного языка привёл к быстрому развитию теории формальных языков (Хомский, 1963; Гинсбург, 1966; Хопкрофт и Ульман, 1979 и другие). Это развитие предоставило интересную возможность для распространения лингвистического подхода в другие области. В частности, возникла идея об аналогичном лингвистическом представлении физических образов (рис.1.5). Эта идея была успешно разработана и воплощена в синтаксических методах распознавания образов (Нарасимхан, 1966; Фу, 1974, 1982; Павлидис, 1977) и языках описания изображений (Шоу, 1969; Федер, 1971; Розенфельд, 1979). Плекс-языки, введеные в (Федер, 1971), продемонстрировали значительную описательную мощь. В обычной строке символов каждый символ связан только с двумя соседями - левым и правым. Поэтому он имеет две точки сцепления. В Плекс-языке символ называется NAPE (n Attaching-Point Entity, т.е. n-связанный объект) и может иметь произвольное число n-точек сцепления для соединения с другими символами. Результирующие слова представляют общие многомерные образы, которые позволяют генерировать образы, представляющие деревья, сложные химические формулы, электрические схемы и т.д. Нечто аналогичное можно было бы сделать в LG с Траекториями и Сетями.
|
|
|
Searching for adequate mathematical tools formalizing heuristics, we transformed the idea of linguistic representation of complex natural and artificial images into the idea of similar representation of complex hierarchical systems (Stilman, 1981, 1984b, 1985a, 1985b, 1985c, 1992). However, the appropriate languages should have had more sophisticated and flexible attributes than languages usually used for pattern description. Origin of such languages can be traced back to research on programmed attribute grammars by Knuth (1968), Rozenkrantz (1969) and others. In this respect, special attention should be paid to the results of N.Volchenkov (1979) and L.Kuzin (1979). Volchenkov developed incredibly powerful generating grammars, which he called BUPPG. A modification and generalization of these grammars (Stilman, 1993a, 1993b) allowed us to generate languages that met all the requirements for representation of dynamic hierarchies. This modification, named controlled grammars (Chapter 8), allowed us to use them as a universal tool on all levels of LG and formally prove correctness and completeness of the generated languages, and evaluate their running time (Chapters 8-12, and 14). A new version of controlled grammars is considered in (Yakhnis V., Yakhnis A. and Stilman B., 1996, 1997).
|
|
|
В поисках адекватных математических инструментов, формализующих эвристику, мы преобразовали идею лингвистического представления сложных естественных и искусственных образов в идею аналогичного представления сложных иерархических систем (Штильман, 1981, 1984b, 1985a, 1985b, 1985c, 1992). Однако соответствующие языки должны были бы иметь более изощрённые и гибкие атрибуты, чем языки, обычно используемые для описания образов. Происхождение таких формальных языков можно проследить ретроспективно, начиная с исследований программируемых и атрибутных грамматик (Кнут, 1968; Розенкранц, 1969 и прочие). В этом отношении, особого внимания заслуживают результаты Н.Волченкова (1979) и Л.Кузина (1979). Волченков разработал исключительно мощные порождающие (генерирующие) грамматики, которые он называет БУППГ. Модификация и обобщение этих грамматик (Штильман, 1993a, 1993b) позволили нам построить языки, которые удовлетворяли всем требованиям для представления динамических иерархий. Эта модификация, названная управляемыми грамматиками (глава 8), позволила использовать их как универсальный инструмент на всех уровнях LG, формально доказывать правильность и полноту построенных языков, оценивать вычислительную сложность их порождения (главы 8-12 и 14). Новая версия управляемых грамматик рассмотрена в (В.Яхнис, А.Яхнис и Б.Штильман, 1996, 1997).
|
|
|
Until the third stage of LG development, in the beginning of the 90s, the formal tools were not organized as a full-scale complete mathematical model. Development of the programs PIONEER at the second stage was based on a collection of heuristic algorithms. Multiple experiments with these programs allowed us to make far reaching generalizations and later construct a mathematical model.
|
|
|
До третьего этапа развития LG, в начале 90-х годов, формальные инструменты ещё не были организованы в полномасштабную математическую модель. Развитие программ ПИОНЕР на втором этапе было основано на наборе эвристических алгоритмов. Многократные эксперименты с этими программами позволили сделать далеко идущие обобщения и позднее построить математическую модель.
|
|
|
|
|
1.9 Stage Three: Modern History
|
|
1.9 Этап 3: Новейшая История
|
|
|
Since 1991, this approach is called Linguistic Geometry (LG), due to the geometrical nature of the discovered heuristics and the mathematical tools of the theory of formal languages used to formalize them. A complete presentation of the two levels of the hierarchy of languages was given in (Stilman, 1993a, 1993b, and 1994d).
|
|
|
С 1991 года этот подход называется Лингвистической Геометрией (LG) из-за геометрической природы обнаруженных эвристик и теории формальных языков, применённой для их формализации. Полная разработка двух уровней иерархии языков была представлена в (Штильман, 1993a, 1993b и 1994d).
|
|
|
In the 70s and 80s, the goals of research were related to the discovery of the most intimate features of expert search heuristics and the development of draft formal tools in order to formalize them. In the 90s, with the establishment of LG, the goals have changed. In the third stage of LG development, the scientific goals are related to the exploration of the limits of efficiency, generality, computational complexity, and accuracy of LG.
|
|
|
В 70-х и 80-х годах цели исследования были связаны с открытием наиболее глубоких особенностей экспертных эвристик перебора и разработкой математических инструментов, которые формализуют эти особенности. В 90-х годах с установлением LG как отдельной области цели изменились. На третьем этапе развития LG научные цели связаны с исследованием пределов эффективности, общности, вычислительной сложности и точности LG.
|
|
|
A partial list of questions for the research on LG in the 90s is as follows. What is going to be the most efficient general structure of the LG applications? Are the higher-dimensional problems really solvable employing LG tools? What would be the impact on the running time if we switch from 2D to 3D problems? How would the running time change if we increase the number of agents and provide them with more advanced moving abilities? Can we solve problems with partially or even totally concurrent moves employing similar formal tools? What is the computational complexity of these problems?
|
|
|
Частичный список вопросов для исследований в области LG в 90-х годах приведен ниже. Какой должна быть наиболее эффективная общая структура программных реализаций LG? Существуют ли задачи высокой размерности, решаемые с использованием LG? Как повлияет на время расчётов переход от двумерных задач к трехмерным задачам? Как изменится время расчётов, если мы увеличим число агентов и обеспечим их более развитыми средствами перемещения? Сможем ли мы решать задачи с частично или даже полностью параллельными ходами, используя аналогичные формальные инструменты? Какова вычислительная сложность этих задач?
|
|
|
Fortunately, and unexpectedly, not only these, but the following additional questions were answered as well. How accurate are the solutions? Can we evaluate and prove a certain level of accuracy? If our proof is constructive, how can we use the same techniques for generating solutions?
|
|
|
К счастью, неожиданно для нас, в этот период мы получили ответы не только на эти, но и на другие дополнительные вопросы. Насколько точны решения LG? Можем ли мы строго оценить (и доказать) определённый уровень точности? Если наше доказательство конструктивно, можно ли использовать ту же самую технику для получения решения (а не только для оценки точности)?
|
|
|
All the programs developed in the 70’s and 80’s within the framework of the project PIONEER were highly problem oriented. They served as implementations of heuristic hierarchies of subsystems for specific problem domains. In the 90s, we began exploration of various software tools and approaches for the implementation of the general hierarchy of formal languages and their applications.
|
|
|
Все программы, разработанные в 70-х и 80-х годах в рамках проекта ПИОНЕР, были в высшей степени проблемно-ориентированными. Они служили реализацией эвристических иерархий подсистем для специфических проблемных областей. В 90-х годах мы начинали исследование различных подходов и программных инструментов для реализации общей иерархии формальных языков и их приложений.
|
|
|
A set of general LG grammars was first implemented at the University of Colorado at Denver in 1993 by D.King and R.Mathews employing CLIPS and C languages, respectively (King, 1993), (Mathews, 1993). While R.Mathews implemented just two levels of the hierarchy, trajectories and Zones, D.King developed a working prototype of the full scale hierarchy of grammars using the CLIPS programming environment. Also, he showed that CLIPS programming tools (Giarratano and Riley, 1998), intended originally for the expert system’s development, demonstrated high efficiency for the quick implementation of the LG grammars. Of course, efficiency at the implementation stage was achieved at the expense of the running time of the application. However, these tools could serve as a platform for the development of prototype versions.
|
|
|
Несколько общих LG-грамматик было впервые реализовано в Университете Колорадо в Денвере в 1993 году Д.Кингом и Р.Матьюсом с использованием языка CLIPS и языка C, соответственно (Кинг, 1993) и (Матьюс, 1993). В то время как Р.Матьюс реализовал только два уровня иерархии - Траектории и Зоны (на C), Д.Кинг разработал прототип полномасштабной иерархии грамматик, используя среду программирования CLIPS. Он показал также, что инструменты программирования CLIPS (Гиарратано и Рилей, 1998), предназначенные первоначально для разработки экспертных систем, продемонстрировали высокую эффективность для быстрой реализации LG-грамматик. Конечно, эффективность на этапе разработки была достигнута за счёт снижения эффективности на этапе исполнения. Однако эти инструменты могут послужить основой для разработки прототипов.
|
|
|
Another direction of research was related to exploration of actual applicability of the general LG tools to various problem domains. In 1995, C.Fletcher implemented the Grammars of shortest and admissible trajectories with generalized relations of reachability employing C++ (Fletcher, 1996), (Fletcher and Stilman, 1997). He applied this tool for the development of the simulation software prototype of robot control in industrial environment. Interpretation of various robot movements via relations of reachability allowed this system to make sub-optimal path planning for robots and avoid collisions with immobile and mobile obstacles. Various versions of this prototype were demonstrated at Sandia National Laboratories, Rockwell Science Center, and at a number of conferences.
|
|
|
Другое направление исследований было связано с выяснением фактической актуальности применимости общих LG-инструментов к различным проблемным областям. В 1995 году C.Флечер реализовал Грамматики кратчайших и допустимых Траекторий с обобщенными отношениями достижимости, используя C++ (Флечер, 1996; Флечер и Штильман, 1997). Он применил этот инструмент для разработки программного прототипа для моделирования управления навигацией робота в индустриальной среде. Интерпретация различных движений робота через отношения достижимости позволила этой системе планировать близкие к оптимальным пути роботов и избегать столкновений с неподвижными и подвижными препятствиями. Различные версии этого прототипа демонстрировались в Сандийской Национальной Лаборатории, Научном Центре Рокуэлла и на множестве конференций.
|
|
|
A domain-oriented version of the LG tools was developed by R.Turek (Turek, 1996 and 1997). He developed highly efficient commercial software for the real-time emergency vehicles’ routing. These vehicles (police, fire, and ambulance) were directed to the place of emergency in response to the 911 phone call. The LG grammars used relations of reachability that reflected traffic impedance on the streets of the city of Aurora, CO. The street maps were retrieved from the geographical information system (GIS), while information about impedance was updated in sub-real time employing information collected by cruising police vehicles. Prototypes of this program were demonstrated at the NASA Goddard Space Flight Center at Greenbelt, MD, and at a number of conferences.
|
|
|
Проблемно-ориентированная версия LG-инструментов была разработана Р.Тюреком (Тюрек, 1996 и 1997). Он разработал очень эффективное коммерческое программное обеспечение, работающее в реальном времени, для прокладки маршрутов для машин экстренной помощи. Эти машины (полиция, пожарные и санитарные машины) направлялись к месту происшествия в ответ на телефонные звонки по номеру 911. LG-грамматики использовали отношения достижимости, которые формально представляли планы улиц и заторы движения на улицах города Авроры (часть Денвера), штат Колорадо. Планы улиц были введены при помощи географической информационной системы (GIS), в то время как информация о заторах обновлялась в реальном времени по данным от приборов, которыми комплектуются транспортные средства автодорожной полиции. Варианты этой программы демонстрировались в NASA в Центре Космических Полетов в Гринбелте, MD, и на нескольких конференциях.
|
|
|
In 1996, D.Wood developed BGF, a universal framework for board game applets, employing Java (Wood, 1996). This tool was intended for the development of advanced interfaces of the LG applications for various problem domains. In 1997-98, the BGF was used by E.Skhisov for the development of his combat simulation tool (Skhisov, 1997).
|
|
|
В 1996 году Д.Вуд разработал BGF - универсальную программную среду для настольных игр в виде апплетов на языке Java (Вуд, 1996). Этот инструмент был предназначен для разработки перспективных интерфейсов для приложений LG в различных проблемных областях. В 1997-98 годах Э.Скисов использовал BGF для дальнейшего совершенствования своего инструмента моделирования военных игр (Скисов, 1997).
|
|
|
Combat simulation tool, the most advanced implementation of the LG algorithms so far, was developed by E.Skhisov in 1997 within the joint project of the University of Colorado at Denver and the University of Denver (Skhisov, 1997), (Skhisov and B.Stilman, 1997, 1998a, and 1998b). His tool generated the full scale hierarchy of languages including a prototype version of the Grammar of Translations, the no-search approach (Chapter 13). This implementation was intended for exploration of novel concepts in LG. In particular, this was the first tool applicable to the problems with concurrent movements of agents. Also, this was the first implementation of LG for the parallel computing environment, a network of computers. Specifically, the Grammar of Trajectories was executed in parallel. Combat simulation tool was implemented in C++ and Java. A new version of the tool is being developed exclusively in Java.
|
|
|
Этот инструмент моделирования военных игр (пока что наиболее полная реализация LG-алгоритмов) был разработан Э.Скисовым в 1997 году в рамках совместного проекта Университета Колорадо в Денвере и Университета Денвера (Скисов, 1997; Скисов и Б.Штильман, 1997, 1998a и 1998b). Его инструмент генерировал полномасштабную иерархию языков, включая предварительную версию Грамматики Переводов, основанную на беспереборном подходе (глава 13). Эта реализация была предназначена для исследования новых подходов в LG. В частности это был первый LG-инструмент, применённый к задачам с параллельным движением агентов. Также, это было первой реализацией LG для параллельной вычислительной среды на основе сети компьютеров. В этой среде вычисление траекторий с помощью Грамматики Траекторий происходило параллельно. Инструмент моделирования военных игр был реализован на C++ и на Java. Новая версия инструмента разрабатывается исключительно на языке Java.
|
|
|
In 1998, the class of problems in which LG is applicable was expanded by inclusion of the problems for the local agents that move with variable speed. This expansion makes the LG models closer to the real world problems. M.Stilman generalized the relations of reachability and modified the Grammar of shortest trajectories for this case (M.Stilman and V.Yakhnis, 1998), (DEF 2.4 and Section 9.10). His C++ implementation of this grammar generated all the shortest paths for an airplane which must avoid flying over certain territories. At the beginning the airplane accelerates, then it courses with a constant speed, and, in the end of the flight, it slows down to land.
|
|
|
В 1998 году класс задач, в которых применима LG, был расширен путём включения задач для локальных агентов, перемещающихся с переменной скоростью. Это расширение приближает модели LG к задачам из реальной жизни. Михаил Штильман обобщил отношения достижимости и изменил Грамматику Кратчайших Траекторий для этого случая (М.Штильман, А.Яхнис и В.Яхнис, 1998), (ОПРЕДЕЛЕНИЕ 2.4 и разд.9.10). Его реализация этой грамматики (на C++) вычисляет все кратчайшие пути для самолёта, который должен избежать пролёта над некоторыми территориями. Вначале самолёт ускоряется, затем идёт по курсу с постоянной скоростью и в конце полета он замедляется, чтобы приземлиться.
|
|
|
Application of LG to the Safety Critical Control Systems, Cruise Missiles Control, Planetary Exploration Vehicles, National Missile Defense (with threat and countermeasure assessments), and Space Combat are currently being considered.
|
|
|
В настоящее время исследуется применение LG к системам управления, где безопасность является критическим параметром. Это системы управления крылатыми ракетами, инопланетными исследовательскими аппаратами, системы национальной противоракетной обороны (с оценкой угрозы и контрмер), а также системы управления космическими военными операциями.
|
|
|
As the general structure and details of the LG implementations become clear, a new project is being considered. A universal LG Testbed will serve as a framework for the development of LG applications by tuning to the specific problem domain. Also, this Testbed will be used for quick testing of new ideas and concepts in LG.
|
|
|
По мере того, как общая структура и детали реализаций LG становятся более понятными, мы приближаемся к осуществлению нового проекта. Универсальный LG-testbad будет служить структурной средой для разработки приложений LG путём настройки на определенную проблемную область. Также, LG-testbad будет использоваться для быстрой проверки новых идей и подходов в LG.
|
|
|
To answer the questions about the limits of applicability and resource requirements of the LG solutions, we developed a number of problems of gradually increased complexity. Some of them were based on the endgames considered in the past,
R.Reti endgame,
G.Nadareishvili endgame, and others. The sequence of problems of gradually increased complexity included problems with 3D and n×n district, greater number of agents, sophisticated mobility, alternating concurrent and totally concurrent movements, etc. Solving these problems with the LG tools should give us a basis for further theoretical investigation.
|
|
|
Чтобы ответить на вопросы о пределах применимости и требованиях к ресурсам для приложений LG, мы разработали набор задач постепенно возрастающей сложности. Некоторые из них были основаны на этюдах, которые рассматривались в прошлом: этюде
Рети, этюде
Надареишвили и других. Последовательность задач постепенно возрастающей сложности включала задачи с трёхмерной областью и областью с переменным размером n×n с большим числом агентов, со сложными параметрами подвижности, с чередующимся параллельным движением и полностью параллельным движением агентов и т.д. Решение этих задач с использованием LG-инструментов должно было обеспечить материал для дальнейших теоретических исследований.
|
|
|
In 1993, the CLIPS-based implementation of the hierarchy of grammars was applied to the problem of optimal control of four robotic vehicles in a 2D space participating in a two-player game. The problem was represented as 2D 4-agent discrete pursuit-evasion game, the 2D/4A problem (Stilman, 1996a, 1997a, and Chapter 3), a version the R.Reti endgame. Conventional approaches require a million move tree to solve it. The LG tools allowed us to find the solution by generating the search tree which included only 46 moves, with the branching factor of 1,65. An interesting result was obtained in 1994, when the 2D/4A problem was generalized for the 3D case, the 3D/4A problem (Stilman, 1994b, 1994c, 1996a, and Chapter 4). The problem was represented as a pursuit-evasion game of space stations that have to reach designated areas in space, and space ships that may intercept stations or prevent interception. The conventional approaches require a trillion move tree to solve it, while the tree generated by the LG tools consisted of merely about 50 moves with the branching factor close to one. Apparently, the LG tools allowed us to eliminate the exponential growth of the running time (with respect to the input) for this class of problems (Section 4.4).
|
|
|
В 1993 году, реализованная на основе CLIPS, иерархия грамматик была применена к задаче оптимального управления четырьмя роботами в двумерном пространстве, участвующими в игре 2-х игроков. Задача была представлена как двумерная дискретная игра уклонения от преследования с 4 агентами - задача 2D/4A (Штильман, 1996a, 1997a и глава 3). В сущности, это была версия этюда Рети. Традиционные подходы требуют, чтобы дерево игры для решения этой задачи содержало миллион ходов. LG-инструменты позволили нам найти решение в виде LG-дерева, которое включало только 46 ходов с показателем ветвления 1,65. Интересный результат был получен в 1994 году, когда задача 2D/4A была обобщена для трёхмерного случая - задача 3D/4A (Штильман, 1994b, 1994c, 1996a и глава 4). Задача была представлена как игра уклонения от преследования космических станций, которые должны достигнуть определённых областей в пространстве, и космических кораблей, которые могут перехватить эти станции или предотвратить перехват. Традиционные подходы требуют, чтобы дерево игры для решения этой задачи содержало триллион ходов, в то время как дерево, сгенерированное LG-инструментами, содержало всего около 50 ходов с коэффициентом ветвления близким к 1. Очевидно, что LG-инструменты позволили нам устранить экспоненциальный рост времени исполнения (относительно входных данных) для этого класса задач (разд.4.4).
|
|
|
Another significant test of the LG tools, involving much larger state space, was conducted for the 2D and 3D pursuit-evasion games, which involve 8 aerospace vehicles with advanced moving abilities (Stilman, 1995a, 1995b, 1997d, and Chapter 5). This was a version of G.Nadareishvili endgame. The depth of the solution and, therefore, the depth of the search, was extremely big, at least 25 moves. Theoretical estimates showed that finding solutions of these problems requires generation of search trees that include approximately 1525 and 3025 moves for the 2D/8A and 3D/8A problems, respectively. To generate a tree of that size is beyond reasonable time constraints of any computer. In contrast, the search trees generated employing the LG tools consist of about 150 moves. The branching factor was just 1,12.
|
|
|
Другой существенный тест для LG-инструментов в задачах со значительно большим пространством состояний проводился для двумерных и трёхмерных игр уклонения от преследования, в которых использовались 8 космических кораблей с необычайно сложными и развитыми возможностями перемещения (Штильман, 1995a, 1995b, 1997d и глава 5). Это была версия этюда Г.Надареишвили. Глубина решения и, соответственно, глубина перебора были чрезвычайно большими, по крайней мере, 25 ходов. Теоретические оценки показали, что для нахождения решения этих задач требуется генерация деревьев игры, которые бы включали приблизительно 1525 и 3025 ходов для задач 2D/8A и 3D/8A соответственно. Генерация дерева такого размера выходит за пределы разумных временных ограничений для любого компьютера. Однако, LG-деревья, сгенерированные LG-инструментами, состояли приблизительно из 150 ходов при коэффициенте ветвления 1,12.
|
|
|
These examples demonstrated significant growth of complexity: the number of vehicles, their moving abilities, the dimension of an operational district, and, especially, the required depth of the search. While the running time of the analysis-of-a-state increased, we can suggest that this is just a low-degree polynomial growth with respect to the length of the input. (The evaluation of the running time is presented in Chapter 14.) The search trees practically did not grow. In all the experiments, the search trees were very small, which allows us to suggest that the size of these trees is also a low-degree polynomial with respect to the input. We can conclude that the total computational requirements of the LG models, which is a product of the running time of the analysis-of-a-state procedure and the size of a tree, is a polynomial.
|
|
|
Эти примеры продемонстрировали существенный рост сложности задач от числа роботов, их способности к перемещению, размерности операционной области и, особенно, от требуемой глубины перебора. По тому, как увеличилась продолжительность анализа каждого состояния, можно предположить, что это был всего лишь полиномиальный рост (низкой степени) относительно длины входа. (Оценка времени исполнения представлена в главе 14). Деревья перебора практически не увеличились. Во всех экспериментах LG-деревья были очень маленькими, что позволяет нам предлагать, что размер этих деревьев также является полиномом низкой степени относительно входа. Можно заключить, что полное время вычислений, которое является произведением размера дерева перебора и времени анализа каждого узла (состояния), для моделей LG растёт как полином.
|
|
|
In the above examples, the mobile entities, aircraft, spacecraft, etc., moved in a serial mode, one entity at a time. Moreover, the movements of the opposing sides alternated. It was desirable to expand the LG approach to the problems with concurrent movements. A formal definition of the class of multiagent systems, where LG is applicable, never included the requirement of serial or alternating moves, however, all the examples included the serial moves only. A new direction for application of LG to multiagent systems with high degree of concurrency was established in 1994 (Stilman, 1995c, 1995d, 1997a, 1997b, and Chapter 6). A new class of games, called multiagent graph-games with simultaneous moves, was developed by V.Yakhnis, and the author (1995). These new games permit simultaneous (concurrent) moves of several cooperating/competing agents; moreover, each super-agent may either skip or move one or more local agents at the same time.
|
|
|
В вышеупомянутых примерах подвижные объекты - самолёты, космические корабли и т.д. - перемещаются последовательно, т.е. один объект за один ход. Кроме того, движения объектов противоположных сторон чередуются. Нам было важно расширить применимость LG, охватив задачи с параллельным перемещением. На разных этапах развития LG формальное определение класса многоагентных систем, в которых применима LG, никогда не включало требования последовательных или чередующихся ходов, однако все примеры включали только последовательные перемещения. Новое направление, связанное с применением LG к многоагентным системам с высокой степенью параллелизма, определилось в 1994 году (Штильман, 1995c, 1995d, 1997a, 1997b и глава 6). Новый класс игр, называемый многоагентными играми на графе с одновременными ходами, был разработан В.Яхнисом и автором (1995). Эти новые игры разрешают одновременные (параллельные) ходы нескольких кооперирующих и конкурирующих агентов; кроме того, каждая сторона (суперагент) может пропустить ход или сделать ход путём одновременного перемещения одного или нескольких локальных агентов.
|
|
|
A number of examples were developed in 1994-95. We gradually increased the level of concurrency while trying to explore its impact on the effectiveness of the LG tools (Chapter 6). Application of LG to the problems with totally concurrent movements was initially funded by the U.S. Air Force within the Summer 1995 Faculty Associateship Program at Phillips Laboratory, Kirtland AFB (Stilman, 1997a). A prototype of the program for the real time generation of the air combat scenario was developed at Phillips Laboratory in 1995. It was intended to control manned and unmanned aerial vehicles guided by the satellite based sensors to detect mobile adversarial missile launchers and destroy them. In 1996, this research was supported by a grant from the Sandia National Laboratories. In these problems, the aircraft, both cooperating and opposing, could move concurrently. These applications involved two opposing teams, two aircraft on each team. Introduction of concurrency resulted in a significant growth of the branching factor - if we apply the brute force search - up to 324. This is the base of the exponent that shows the size of the search trees to be generated. In contrast, the search tree generated by the LG tools for this totally concurrent model contains just 40 moves with the branching factor of about 1,5. Later, these results were generalized for an n×n district, (Stilman and Fletcher, 1998, and Chapters 6, 13, and 14).
|
|
|
Несколько примеров было разработано в 1994-95 годах. Мы постепенно увеличивали степень параллелизма, выясняя его воздействие на эффективность LG-инструментов (глава 6). Применение LG к задачам с полностью параллельными движениями первоначально финансировалось американскими ВВС в 1995 году в рамках летней программы для профессоров на базе Лаборатории Филипса, расположенной на Военно-Воздушной Базе Кэртланд (Штильман, 1997a). Прототип программы для генерации сценария воздушного боя в режиме реального времени был разработан в Лаборатории Филипса в 1995 году. Эта программа была предназначена для управления пилотируемыми и беспилотными самолётами, наводимыми датчиками, установленными на спутниках, для обнаружения и уничтожения подвижных вражеских пусковых установок ракет. В 1996 году эти исследования финансировались грантом от Сандийской Национальной Лаборатории. В этих задачах самолеты - свои и противника - могли летать одновременно. Разработанные задачи включали две противостоящих группы, по два самолёта в каждой группе. Введение параллелизма привело к существенному росту коэффициента ветвления, до 324 (если применять перебор по методу «брут форс»). Это число - основание степени при экспоненциальном законе роста размера дерева игры, которое должно быть построено. Однако, LG-дерево для этой полностью параллельной модели содержит только 40 ходов с коэффициентом ветвления примерно 1,5. Позже эти результаты были обобщены для n×n области (Штильман и Флечер, 1998; и главы 6, 13 и 14).
|
|
|
While introduction of concurrency has a profound impact on the running time of conventional algorithms, it appears not to be the case with the LG solutions. Apparently, this means that the LG tools allowed us to identify a subclass of low (polynomial) complexity problems in the class of problems that are usually considered as computationally hard. This subclass includes not only serial but concurrent problems as well (Chapters 13 and 14). A deeper investigation of these issues is forthcoming.
|
|
|
В то время как введение параллелизма оказывает решающее влияние на время исполнения при использовании традиционных алгоритмов, этого, кажется, не происходит при использовании LG. Это означает, что LG-инструменты позволили выделить подкласс низких (полиномиальных) по сложности задач в классе задач, которые обычно рассматривались в вычислительном отношении как трудноразрешимые. Новый подкласс включает не только последовательные, но также и параллельные задачи (главы 13 и 14). Более глубокое исследование этих вопросов нам предстоит в будущем.
|
|
|
One of the latest achievements in LG is the mathematical proof of optimality of the solutions obtained for some classes of problems, including the so-called Reti-like combat simulation problems (Stilman, 1996b, 1997c, 1997d). This investigation was supported by a grant from the Sandia National Laboratories. This result, obtained in 1996 and later improved, still looks amazing for those involved in research on LG. During the entire history of the development of LG, the major concern was how to demonstrate the quality of the approximate solutions, almost winning strategies, e.g., how to measure their accuracy. As it was discussed earlier, these were solutions approved by experts. Existence of an error was not even in question because heuristic algorithms usually do not guarantee optimum. For years we have tried to come up with a measure of this error. Surprisingly, this research resulted in a proof of no error for the Reti-like problems (Section 13.9). This new result tells us that the LG tools generate optimal solutions for a class of search problems. Optimality means that the result is the same as the solution, which could be obtained using the exhaustive search.
|
|
|
Одно из последних достижений в LG - математическое доказательство оптимальности решений, полученных для некоторого класса задач, содержащего так называемые Рети-подобные задачи моделирования военных игр (Штильман, 1996b, 1997c, 1997d). Эти исследования финансировались грантом от Сандийской Национальной Лаборатории. Результат, полученный в 1996 году и позднее улучшенный, всё ещё выглядит удивительным для тех, кто вовлечён в исследования по LG. На протяжении всей истории развития LG значительные трудности виделись в том, как продемонстрировать качество приближённых решений, т.е. хороших или почти выигрышных стратегий, например, как измерить их точность. Как уже обсуждалось выше, это были решения одобренные экспертами. Существование ошибки даже не вызывало сомнений, потому что эвристические алгоритмы обычно не гарантируют оптимум. В течение многих лет мы пытались понять, как оценить степень этой ошибки. Удивительно, что эти исследования привели к доказательству отсутствия ошибки для Рети-подобных задач (разд.13.9). Этот новый результат свидетельствует о том, что LG-инструменты генерируют оптимальные решения для подкласса переборных задач. Оптимальность означает, что результат совпадает с решением, которое могло бы быть получено при использовании полного перебора по методу «брут форс».
|
|
|
The most interesting feature of this proof is that it is constructive. The proof is based on a decomposition of the State Space into subsets of states and a construction of the set of paths between these subsets. Every path represents an intend-to-win LG strategy for one of the super-agents. This set of paths is the full set of strategy-candidates. Then some of the candidates are pruned as non-implementable. An attempt of implementation of the rest of the strategy-candidates, the best left for each side, will result in the actual construction of the solution, the (optimal) strategy for this problem. Two solutions, the one constructed in the proof, and the original generated by the LG tools, are the same. However, the new solution, obtained by construction of strategies, does not use any tree-based search. Moreover, it is provably optimal.
|
|
|
Самая интересная особенность этого доказательства состоит в том, что оно является конструктивным. Доказательство основано на декомпозиции Пространства Состояний (т.е. ДИ) на подпространства и построении множества путей между этими подпространствами. Каждый путь представляет потенциально выигрышную LG-стратегию для одного из суперагентов. Множество путей образует полное множество стратегий-кандидатов. Затем некоторые из стратегий-кандидатов отбрасываются как нереализуемые. Попытка реализации оставшихся стратегий-кандидатов, лучших для каждой из сторон, заканчивается фактическим построением решения - выбором (оптимальной) стратегии для этой задачи. Два решения, 1-е, построенное в процессе доказательства, и 2-е оригинальное, сгенерированное ранее LG-инструментами, совпадают. Однако, новое решение, полученное (в процессе доказательства) построением LG-стратегий, не использует вообще никакого перебора на дереве (т.к. не генерирует LG-дерева). Кроме того, оно доказуемо оптимально.
|
|
|
It was desirable to convert this proof into the pure construction of solutions. This was accomplished in 1998 (Stilman, 1998a, 1998b, and Chapter 13). It was named a no-search approach. This approach was expanded to problems with concurrent movements of agents. A combat simulation tool developed by E.Skhisov was used first for experiments with concurrent problems employing the no-search approach (Skhisov and Stilman, 1998a and 1998b). The problems were solved with the branching factor equal exactly to one, i.e., without branching to different directions.
|
|
|
В этой связи возникла мысль о конверсии доказательства в прямое построение LG-решений. Это было достигнуто в 1998 году (Штильман, 1998a, 1998b; и глава 13). Новый метод был назван беспереборным подходом. Беспереборной подход был расширен для охвата задач с параллельным движением агентов. Инструмент моделирования военных игр, разработанный Э.Скисовым, был впервые применён для экспериментов с параллельными задачами на основе беспереборного подхода (Скисов и Штильман, 1998a и 1998b). Задачи были решены с коэффициентом ветвления, равным точно 1, т.е. без ветвления в других направлениях.
|
|
|
At the moment, we have two versions of the top level of the LG algorithm, the Grammar of Translations and the no-search algorithm. The former is a universal tool applicable to various problems. However, it generates a search tree, though small, and does not provide a formal basis for a conclusion about the accuracy of the solution; usually, it generates best known solutions. On the other hand, the no-search algorithm generates a provably optimal solution, a winning strategy, without any tree-based search, but at the moment it is only applicable to a subclass of problems. Note that the term "no-search approach" means that the tree-based search has been eliminated, but the algorithm may still include some other types of searches, e.g., polynomial-time searches. It is likely that the future research based on the expansion of the no-search approach will cause redevelopment of the top level of hierarchy of languages, the Language of Translations.
|
|
|
В настоящее время разработаны две версии верхнего уровня LG-алгоритма: Грамматика Переводов и Беспереборной Алгоритм. Первый является универсальным инструментом, применимым к различным задачам. Генерируя маленькое LG-дерево перебора, он не даёт формальных оснований для заключения о точности решения; обычно, он генерирует решения, которые являются лучшими среди известных. С другой стороны, Беспереборной Алгоритм генерирует доказуемо оптимальное решение - выигрышную стратегию без перебора на дереве, но в настоящее время он применим только к подклассу Рети-подобных задач. Обратите внимание, что термин "беспереборной подход" означает, что перебор на дереве устранён, но Алгоритм всё ещё может включать некоторые другие типы перебора, например, полиномиальные по времени переборы. Вероятно, будущие исследования, основанные на развитии беспереборного подхода, приведут к перестройке верхнего уровня иерархии языков - Языка Переводов.
|
|
|
Besides the problems with mobile entities and opposing sides (such as robot simulation), the LG tools can be effectively applied to the problems without explicit conflict and opposing sides, e.g., to scheduling problems with resource allocation. The foundations of this approach are related to applications of project PIONEER to scheduling and planning at the Stage One of LG development (Section 1.7). To apply the LG tools, we introduce an artificial two-player game, i.e., artificial conflict, operational district, mobile entities, and opposing agents (Stilman and Fletcher, 1998, and Chapter 7). This formulation allows us to solve a number of problems of much higher dimension, which are intractable employing conventional approaches.
|
|
|
Помимо задач с подвижными объектами и противоположными сторонами (типа моделирования навигации робота), LG-инструменты могут быть эффективно применены к задачам без явного конфликта и противоположных сторон, например, к задаче составления расписаний с распределением ресурсов. Основы этого подхода были заложены применениями проекта ПИОНЕР к составлению графиков ремонтов и планированию на 1-м этапе развития LG (разд.1.7). Чтобы применить LG-инструменты, мы вводим искусственную игру двух игроков, т.е. искусственный конфликт, операционную область, подвижные объекты и противоборствующие стороны (Штильман и Флетчер, 1998, и глава 7). Эта формулировка позволила нам решить задачи высокой размерности, которые были неразрешимы при использовании традиционных подходов.
|
|
|
|
|
|
|
ЛИТЕРАТУРА
и интернет-ссылки
|
|
Albus, J. (1991). "Outline for a Theory of Intelligence", IEEE Trans. on Systems, Man and Cybernetics, 1991, No.3, pp.473-509.
|
|
Эльбас Дж. (1991), "Outline for a Theory of Intelligence", IEEE Trans. on Systems, Man and Cybernetics, 1991, No.3, pp.473-509.
|
|
|
Allen, J.F. (1984). "Towards a general theory of action and time", Artificial Intelligence, 1984, No.23, pp.123-154.
|
|
|
Аллен Дж.Ф. (1984), "Towards a general theory of action and time", Artificial Intelligence, 1984, No.23, pp.123-154.
|
|
|
Berge, C. (1957). "Topological Games with Perfect Information", Contributions to the Theory of Games, III, Annals of Mathematical Studies, 1957, No.39, pp.165-.., Princeton, NJ.
|
|
|
Берж C. (1957), "Topological Games with Perfect Information", Contributions to the Theory of Games, III, Annals of Mathematical Studies, 1957, No.39, pp.165-170, Princeton, NJ.
|
|
|
Boddy, M., Dean, T. (1989). "Solving Time-Dependent Planning Problems", Proc. of the 11th Int. Joint Conf. on AI, 1989, pp.979-984.
|
|
|
Боди M., Диан T. (1989), "Solving Time-Dependent Planning Problems", Proc. of the 11th Int. Joint Conf. on AI, 1989, pp.979-984.
|
|
Botvinnik, M.M. (1961). "Lyudy i Mashiny za Shakhmatnoi Doskoi" (Men and Computers at the Chess Board), Shakhmaty v SSSR (Chess in the USSR), 1961, No.3, Moscow (in Russian).
|
|
Ботвинник М.М. (1961). "Люди и машины за шахматной доской", Шахматы в СССР, 1961, № 3, Москва, (см. также Ботвинник М.М., 1987).
|
|
Botvinnik, M.M. (1968). Algoritm igry v Shakhmaty (Algorithm for Playing Chess), "Nauka", Moscow, 1968, 93 pp., 25000 copies, (in Russian).
Botvinnik, M.M. (1970). Chess, Computers and Long-Range Planning, Springer-Verlag, Berlin, Heidelberg, and New York, 1970, (Translated from Russian Botvinnik M.M., 1968 into English).
|
|
Ботвинник М.М. (1968). Алгоритм игры в шахматы, "Наука", Москва, 1968, 93 стр., 25 тыс. экз.
Ботвинник М.М. (1970), Chess, Computers and Long-Range Planning, Springer-Verlag, Berlin, Heidelberg, and New York, 1970, (перевод с русского Ботвинник М.М., 1968 на английский).
|
|
|
Botvinnik, M.M. (1972). Block-schema Algoritma Igry v Shakhmaty (A Flow Chart of Algorithm for Playing Chess), The USSR Academy of Sciences: Scientific Board for Complex Problem «Cybernetics», Moscow, 1972, 28 pp., (in Russian).
|
|
|
Ботвинник М.М. (1972). Блок-схема алгоритма игры в шахматы, АН СССР: Научная секция по комплексной проблеме «Кибернетика», Москва, 1972, 28 стр.
|
|
|
Botvinnik, M.M. (1973). O Kiberneticheskoi Cely Shakhmatnoi Igry (On the Cybernetic Goal of the Game of Chess), The USSR Academy of Sciences: Scientific Board for Complex Problem «Cybernetics», Moscow, 1973, 40 pp., (in Russian).
|
|
Ботвинник М.М. (1973). О кибернетической цели шахматной игры, АН СССР: Научная секция по комплексной проблеме «Кибернетика», Москва 1973, 40 стр.
Ботвинник М.М. (1974). "Шахматы и компьютеры", Правда, Август 17, 1974, Москва, (см. также Ботвинник М.М., 1987).
|
|
|
|
|
|
Botvinnik, M.M. (1977). "PIONEER gotovitsia k championatu" (PIONEER is Preparing for the Championship), Pravda, November 24, 1977, Moscow, (in Russian).
|
|
|
|
Botvinnik, M.M., Stilman, B., Yudin, A.D. (1978). "Iskusstvennyi Shakhmatnyi Master" (Artificial Chess Master), Vestnik Academyi Nauk SSSR (Reports of the Presidium of the USSR Academy of Sciences), 1978, No.4, pp.82-91, Moscow, (in Russian).
|
|
|
|
|
|
|
Botvinnik, M.M. (1979). O Resheniy Netochnih Perebornikh Zadach (On Solving Inexact Search Problems), "Sovetskoe Radio", Moscow, 1979, 149 pp., 15000 copies, (in Russian).
|
|
|
|
Botvinnik, M.M. (1980a). "Metodom «boziey korovky»" (Following the ladybug approach ...), Junost, No.8, 1980, pp.107-109, Moscow, (in Russian).
|
|
|
|
Botvinnik, M.M. (1980b). "Robot nachinaet i ..." (Robot begins and ...), Komsomolskaya Pravda, April 24, 1980, Moscow, (in Russian).
|
|
|
|
Botvinnik, M.M., Stilman, B., Yudin, A.D., Reznitskiy, A.I., Tsfasman, M.A. (1980). "Thinking of Man and Computer", Preprint of the 2nd Int. Meeting on Artificial Intelligence, 9 pp., Repino, Leningrad, Russia, Oct. 1980.
|
|
Ботвинник М.М., Штильман Б.М., Юдин А.Д., Резницкий А.И., Цфасман М.А. (1980). "О шахматистах и компьютерах", Препринт для 2-го Международного симпозиума по Искусственному Интеллекту, 9 стр., Репино, Ленинград, Россия, октябрь 1980.
Ботвинник М.М. (1981). "Зачем ЭВМ играет в шахматы", Правда, Март 30, 1981, Москва, (см. также Ботвинник М.М., 1987).
|
|
|
Botvinnik, M.M. (1982). Meine neuen Ideen zur Shachprogrammierung (My New Ideas on Computer Chess Programming), Springer-Verlag, Berlin, Heidelberg, and New York, 177 pp., 1982, (Translated from Russian Botvinnik M.M., 1979 into German).
|
|
Ботвинник М.М. (1982), Meine neuen Ideen zur Shachprogrammierung (My New Ideas on Computer Chess Programming), Springer-Verlag, Berlin, Heidelberg, and New York, 177 pp., 1982, (перевод с русского Ботвинник М.М., 1979 на немецкий).
Ботвинник М.М. (1983). "Шахматная игра - прошлое, настящее, будущее", журнал Международной ассоциации компьютерных шахмат, № 1, 1983, Амстердам, (см. также Ботвинник М.М., 1987).
|
|
|
|
|
|
Botvinnik, M.M., Petriyev, E., Reznitskiy, A.I., Syutkin, B.D., Timofeev, Y.I., Ulanov, G.A. (1983). "Primenenie novogo metoda dlia reshenia perebornikh zadach dlia planirovania remontov energooborudovania" (Application of New Method for Solving Search Problems to Schedulin of Power Equipment Maintenance), Economics and Mathematical Methods, Moscow, 1983, vol.19, No.6, pp.1030-1041, (in Russian).
|
|
|
Ботвинник М.М., Петряев Е., Резницкий А.И., Сюткин Б.Д., Тимофеев Я.И., Уланов Г.А. (1983). "Применение нового метода решения переборных задач к планирования ремонтов оборудования электростанций", Экономика и математические методы, Москва, 1983, т.19, вып.6, стр.1030-1041, (см. также Ботвинник М.М., 1989).
|
|
|
Botvinnik, M.M. (1984). Computers in Chess: Solving inexact search problems, Springer Series in Symbolic Computation, with Appendixes, Springer-Verlag, New York, 158 pp., 1984, (Translated from Russian Botvinnik M.M., 1979 into English).
|
|
Ботвинник М.М. (1984).
Botvinnik, M.M. (1984), Computers in Chess: Solving inexact search problems, Springer Series in Symbolic Computation, with Appendixes, Springer-Verlag, New York, 158 pp., 1984, (перевод с русского Ботвинник M.M., 1979 на английский).
Ботвинник М.М. (1984a).
Аналитические и критические работы 1923-1941
,
"Физкультура и спорт", Москва, 1984, 320 стр., 120 тыс. экз.
Ботвинник М.М. (1985).
Аналитические и критические работы 1942-1956
,
"Физкультура и спорт", Москва, 1985, 400 стр., 120 тыс. экз.
Ботвинник М.М. (1986).
Аналитические и критические работы 1957-1970,
,
"Физкультура и спорт", Москва, 1986, 368 стр., 120 тыс. экз.
Ботвинник М.М. (1987).
Аналитические и критические работы 1928-1986. Статьи. Воспоминания
,
"Физкультура и спорт", Москва, 1987, 528 стр.
Ботвинник М.М. (1987a). "Об искусственном шахматном мастере", (в кн. Ботвинник М.М., 1987).
Ботвинник М.М. (1987b). "Шахматы и принятие решений", (в кн. Ботвинник М.М., 1987).
Ботвинник М.М. (1987c). "О шахматистах и компьютерах", Предисловие к книге Г.Опферманна "Успехи больших шахматных мыслителей", на нем. языке, (в кн. Ботвинник М.М., 1987).
Ботвинник М.М. (1987d). "Роль Греко в развитии шахмат", (в кн. Ботвинник М.М., 1987).
|
|
Botvinnik, M.M. (1989).
Chess metod resheniya perebornyh zadach
,
"Sovetskiy Sport", Moscow, 1989, 112 pp., 15000 copies, (in Russian).
Botvinnik, M.M. (1997). У цели, Москва, 1997.
|
|
|
|
|
|
|
Chapman, D. (1987). "Planning for conjunctive goals", Artificial Intelligence, 1987, No.32(3).
|
|
|
Чэпман Д. (1987), "Planning for conjunctive goals", Artificial Intelligence, 1987, No.32(3).
|
|
|
Chomsky, N. (1963). "Formal Properties of Grammars", in Handbook of Mathematical Psychology, eds. R.Luce, R.Bush, E. Galanter., vol. 2, John Wiley & Sons, New York: Wiley, 1963, pp.323-418.
|
|
Хомский Н. (1963), "Formal Properties of Grammars", in Handbook of Mathematical Psychology, eds. R.Luce, R.Bush, E. Galanter., vol. 2, John Wiley & Sons, New York: Wiley, 1963, pp.323-418.
Хомский Н. (1966). "Формальные свойства грамматик", Кибернетический сборник, Москва, 1966, № 2, стр.121-230.
(
см. также
Кузин Л.Т., 1979
Кузнецов О.П., Адельсон-Вельский Г.М., 1988
Лорьер Ж.-Л., 1991
)
|
|
|
|
|
|
|
|
|
Drabble, B. (1991). "Spacecraft Command and Control Using Artificial Intelligence Techniques", J. of the British Interplanetary Society, 1991, vol. 44, pp.251-254.
|
|
|
Драббле Б. (1991), "Spacecraft Command and Control Using Artificial Intelligence Techniques", J. of the British Interplanetary Society, 1991, vol. 44, pp.251-254.
|
|
|
Feder, J. (1971). "Plex languages", Information Sciences, 1971, No.3, p.225-241.
|
|
|
Федер Дж. (1971), "Plex languages", Information Sciences, 1971, No.3, pp.225-241.
|
|
|
Fikes, R.E., Nilsson, N.J. (1971). "STRIPS: A New Approach to the Application of Theorem Proving in Problem Solving", Artificial Intelligence, 1971, No.2, pp.189-208.
|
|
Файкс Р., Нильсон Н. (1971), "STRIPS: A New Approach to the Application of Theorem Proving in Problem Solving", Artificial Intelligence, 1971, No.2, pp.189-208.
Файкс Р., Нильсон Н. (1971). "Система STRIPS — новый подход к применению методов доказательства теорем при решении задач", в сб. Интегральные роботы, вып. 1. Под ред. Г.Е.Поздняка, Москва, 197.., стр.82-103.
(
см. также
Кузин Л.Т., 1979
Лорьер Ж.-Л., 1991
)
|
|
|
Fletcher, C. (1996). "Linguistic Geometry Methods for Autonomous Mobile Robot Control", Thesis, University of Colorodo at Denver, 1996.
|
|
|
Флечер C. (1996), "Linguistic Geometry Methods for Autonomous Mobile Robot Control", Thesis, University of Colorodo at Denver, 1996.
|
|
|
Fletcher, C., Stilman, B. (1997). "Linguistic Geometry for Robot Control", Proc. of the 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Germany, Aug., 1997, pp.521-526.
|
|
|
Флечер C., Штильман Б. (1997), "Linguistic Geometry for Robot Control", Proc. of the 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Germany, Aug., 1997, pp.521-526.
|
|
|
|
|
Фу Н. (1996).
Foo, N. (1996). Private Communication of November 13, 1996.
|
|
|
Fu, K.S. (1974). Syntactic Methods in Pattern Recognition, Academic Press, New York and London, 1974.
|
|
Фу K.С. (1974).
Fu, K.S. (1974). Syntactic Methods in Pattern Recognition, Academic Press, New York and London, 1974.
Фу К. (1977). Структурные методы в распознавании образов, Москва, "Мир", 1977, 320 стр.
|
|
|
Fu, K.S. (1982). Syntactic Pattern Recognition and Applications, Prentice Hall, Englewood Cliffs, 1982.
|
|
|
Фу K.С. (1982), Syntactic Pattern Recognition and Applications, Prentice Hall, Englewood Cliffs, 1982.
|
|
|
Gale, D., Stewart, F. M. (1953). "Infinite Games with Perfect Information", Contributions to the theory of games, Annals of Math. Studies, No. 28, Princeton Univ. Press, pp. 245-266, 1953.
|
|
|
Гейл Д., Стюарт Ф.М. (1953), "Infinite Games with Perfect Information", Contributions to the theory of games, Annals of Math. Studies, No. 28, Princeton Univ. Press, pp. 245-266, 1953.
|
|
|
Garcia-Ortiz, A., Wootton, J., Rodin, E.Y., Amin, S.M., Meusey, ., Ruan, C., Wu, A.Y., De, P., Revetta, J. (1993). "Application of Semantic Control to a Class of Pursue-Evader Problems", Computers and Mathematics with Applications, 1993, No.26(5), pp.97-124.
|
|
|
|
Garey, M.R., Johnson D.S. (1991). Computers and Intractability: A Guide to the Theory of NP-Completeness, (Bell Laboratories, Murray Hill, New Jersey), W.H. Freeman and Company, San Francisco, 1991.
|
|
Гэри М., Джонсон Д. (1991), Computers and Intractability: A Guide to the Theory of NP-Completeness, (Bell Laboratories, Murray Hill, New Jersey), W.H. Freeman and Company, San Francisco, 1991.
Гэри М., Джонсон Д. (1982). Вычислительные машины и труднорешаемые задачи, Москва, "Мир", 1982, 416 стр., 8 тыс. экз.
|
|
Georgeff, M.P. (1983). "Communication and Interaction in Multiagent Planning", Proc. of the 3d AAAI Conf., Washington, DC, 1983, pp.125-129.
Georgeff, M.P. (1990). "Planning", in Readings in Planning, Morgan Kauffmann, San Mateo, CA, 1990, pp.5-25.
|
|
Георгев M.П. (1983), "Communication and Interaction in Multiagent Planning", Proc. of the 3d AAAI Conf., Washington, DC, 1983, pp.125-129.
Георгев M.П. (1990), "Planning", in Readings in Planning, Morgan Kauffmann, San Mateo, CA, 1990, pp.5-25.
|
|
|
Ginsburg, S. (1966). The Mathematical Theory of Context-Free Languages, McGraw Hill, New York, 1966.
|
|
Гинзбург С. (1966), The Mathematical Theory of Context-Free Languages, McGraw Hill, New York, 1966.
Гинзбург С. (1970). Математическая теория контекстно-свободных языков, Москва, "Мир", 1970.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hsu, F-h., Anantharaman, T.S., Campbell M.S., Nowatzyk, A. (1990). "Deep Thought", in Computers, Chess, and Cognition, Ed. by Marsland, T.A., Schaeffer, J., Springer-Verlag, New York, 1990, pp.55-78.
|
|
|
Хсу Ф., и др. (1990), "Deep Thought", in Computers, Chess, and Cognition, Ed. by Marsland, T.A., Schaeffer, J., Springer-Verlag, New York, 1990, pp.55-78.
|
|
|
|
Хопкрофт Дж., Ульман Дж. (1979), Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, Reading, MA, 1979.
Хопкрофт Дж., Ульман Дж. (2002). Введение в теорию автоматов, языков и вычислений, С-Петербург, 2002.
(
см. также
Ахо А., Ульман Дж., 1978a, 1978b
Ахо А., Хопкрофт Дж., Ульман Дж., 1979
Рэйнгольд Э., Нивергельд Ю., Део Н., 1980
)
|
|
|
|
|
|
Kaindl, H. (1990). "Tree Search Algorithms", in Computers, Chess, and Cognition, Ed. by Marsland, T.A., Schaeffer, J., Springer-Verlag, New York, 1990, pp.133-158.
|
|
|
Кэйндл Х. (1990), "Tree Search Algorithms", in Computers, Chess, and Cognition, Ed. by Marsland, T.A., Schaeffer, J., Springer-Verlag, New York, 1990, pp.133-158.
|
|
|
King, D. (1993). "Rule Based Approach to Hierarchical Grammars for Geometrical Reasoning", M.S. Thesis, 1993, 141 pp., Dept. of Computer Science, University of Colorado at Denver.
|
|
|
Кинг Д. (1993), "Rule Based Approach to Hierarchical Grammars for Geometrical Reasoning", M.S. Thesis, 1993, 141 pp., Dept. of Computer Science, University of Colorado at Denver.
|
|
|
Khenkin, V. (1977). "An Algorithm for Chess", in Soviet Union, May 1977, No.6(327), pp.46-47, (see also reprint: "A Russian Algorithm for Chess", Personal Computing, June 1979, pp.77-79).
|
|
|
Хенкин В. (1977). "Алгоритм для шахматной игры", в жур. Советский Союз, Май 1977, № 6(327), стр.46-47.
|
|
|
Knoblock, C.A. (1990). "Learning Abstraction Hierarchies for Problem Solving", Proc. of the 8th AAAI Conf., Menlo Park, CA, 1990, pp.923-928.
|
|
|
Кноблок C.A. (1990), "Learning Abstraction Hierarchies for Problem Solving", Proc. of the 8th AAAI Conf., Menlo Park, CA, 1990, pp.923-928.
|
|
|
Knuth, D.E. (1968). "Semantics of Context-Free Languages", Mathematical Systems Theory, 1968, No.2, pp.127-146.
|
|
Кнут Д.Э. (1968), "Semantics of Context-Free Languages", Mathematical Systems Theory, 1968, No.2, pp.127-146.
Кнут Д.Э. (1978). "Семантика контекстно-свободных языков", в сб. Семантика языков программировния, Москва, "Мир", 1978.
|
|
|
|
|
|
Korf, R.E. (1987). "Planning as Search: A Quantitative Approach", Artificial Intelligence, 1987, No.33, pp.65-88.
|
|
|
Корф Р.Э. (1987), "Planning as Search: A Quantitative Approach", Artificial Intelligence, 1987, No.33, pp.65-88.
|
|
|
Korf, R.E. (1987). "Planning as Search: A Quantitative Approach", Artificial Intelligence, 1987, No.33, pp.65-88.
|
|
|
Корф Р.Э. (1987), "Planning as Search: A Quantitative Approach", Artificial Intelligence, 1987, No.33, pp.65-88.
|
|
|
Kuhn, H.W. (1953). "Extensive Games and the Problem of Information", Contributions to the Theory of Games, II, Annals of Mathematical Studies, Princeton, NJ, 1953, No.28, pp.193-216.
|
|
|
Кун Х. (1953), "Extensive Games and the Problem of Information", Contributions to the Theory of Games, II, Annals of Mathematical Studies, Princeton, NJ, 1953, No.28, pp.193-216.
|
|
|
Kuzin, L.T. (1979). Osnovy kibernetiky (Foundations of Cybernetics), vol. 2, "Energia", Moscow, 1979, 584 pp. (in Russian).
|
|
|
Кузин Л.Т.(1979). Основы кибернетики, том 2. Основы кибернетических моделей, "Энергия", Москва, 1979, 584 стр., 27 тыс. экз.
|
|
|
|
|
|
Leitmann, G. (1990). Optimization Techniques with Applications to Aerospace Systems, Academic Press, 1990.
|
|
|
Лейтман Г. (1990), Optimization Techniques with Applications to Aerospace Systems, Academic Press, 1990.
|
|
|
Lirov Y., Rodin, E.Y., McElhaney, B.G., Wilbur, L.W. (1988). "Artificial Intelligence Modeling of Control Systems", Simulation, 1988, No.50(1), pp.12-24.
|
|
|
|
|
|
|
|
|
|
Mathews E.R. (1993). "An Implementation of the Grammars of Trajectories and Zones in C Language", M.B.S. Thesis, Dept. of Mathematics, University of Colorado at Denver, 1993.
|
|
|
Матьюс Э.Р. (1993), "An Implementation of the Grammars of Trajectories and Zones in C Language", M.B.S. Thesis, Dept. of Mathematics, University of Colorado at Denver, 1993.
|
|
|
|
|
McCarthy, J. (1980). "Circumscription - A Form of Non-Monotonic Reasoning", Artificial Intelligence, 1980, No.13, pp.27-39.
McCarthy, J. (1990). "Chess as the Drosophila of AI", in Computers, Chess, and Cognition, Ed. by Marsland, T.A., Schaeffer, J., Springer-Verlag, New York, 1990, pp.227-237.
McCarthy, J. (1997). "AI as Sport, Review of (Newborn, 1996)", Science, June 6, 1997, No.276, pp.1518-1519.
McCarthy, J. (1998). "«Computer Chess» and human chess".
McCarthy, J., Hayes, P.J. (1969). "Some Philosophical Problems from the Standpoint of Artificial Intelligence", Machine Intelligence, 1969, No.4, pp.463-502.
|
|
МакКарти Дж. (1980), "Circumscription - A Form of Non-Monotonic Reasoning", Artificial Intelligence, 1980, No.13, pp.27-39.
МакКарти Дж. (1990), "Chess as the Drosophila of AI", in Computers, Chess, and Cognition, Ed. by Marsland, T.A., Schaeffer, J., Springer-Verlag, New York, 1990, pp.227-237.
МакКарти Дж. (1997), "AI as Sport, Review of (Newborn, 1996)", Science, June 6, 1997, No.276, pp.1518-1519.
МакКарти Дж. (1998), "«Computer Chess» and human chess".
МакКарти Дж., Хайес П.Дж. (1969), "Some Philosophical Problems from the Standpoint of Artificial Intelligence", Machine Intelligence, 1969, No.4, pp.463-502.
|
|
|
McDermott, D. (1985). "Reasoning about Plans", in Formal Theories in the Commonsense World, Ed. J.R.Hobbs, R.C.Moore, Ablex, Norwood, NJ, 1985, pp.269-317.
|
|
|
МакДермот Д. (1985), "Reasoning about Plans", in Formal Theories in the Commonsense World, Ed. J.R.Hobbs, R.C.Moore, Ablex, Norwood, NJ, 1985, pp.269-317.
|
|
|
McNaughton, R. (1993). "Infinite Games Played on Finite Graphs", Annals of Pure and Applied Logic, 1993, vol. 65, pp.149-184.
|
|
|
МакНотон Р. (1993), "Infinite Games Played on Finite Graphs", Annals of Pure and Applied Logic, 1993, vol. 65, pp.149-184.
|
|
|
|
|
Meystel, A. (1995). Semiotic Modeling and Situation Analysis: An Introduction, AdRem Inc., Bala Cynwyd, PA, 1995.
Meystel, A. (1996a). "Intelligent System: A Semiotic Perspective", Int. Journal of Intelligent Control and Systems, 1996, No.1(1), pp.31-57.
Meystel, A. (1996b). "Evolution of Knowledge in Large Complex Systems: An Extended Abstract", Proc. of the 1996 Int. Workshop on Control Mechanisms for Complex Systems, Las Cruces, NM, Dec. 1996, pp.231-254.
Meystel, A. (1998). Private Communication, December, 1998.
|
|
Майстел A. (1995), Semiotic Modeling and Situation Analysis: An Introduction, AdRem Inc., Bala Cynwyd, PA, 1995.
Майстел A. (1996a), "Intelligent System: A Semiotic Perspective", Int. Journal of Intelligent Control and Systems, 1996, No.1(1), pp.31-57.
Майстел A. (1996b), "Evolution of Knowledge in Large Complex Systems: An Extended Abstract", Proc. of the 1996 Int. Workshop on Control Mechanisms for Complex Systems, Las Cruces, NM, Dec. 1996, pp.231-254.
Майстел A. (1998), Private Communication, December, 1998.
|
|
|
Mirniy, V.R., Chudakov, M.V., Stilman, B. (1988). "ARM Programmista na osnove integrirovannoi systemy upravlenia versii program" (Programmer's Workbench on the Basis of Integrated System for Software Configuration Management), Programmnaia Ingeneria (Software Engineering), MDNTP im.Dzerginskogo, Moscow, 1988, pp.59-65 (in Russian).
|
|
|
|
Mirniy, V.R., Roizner, A.G., Chudakov, M.V., Stilman, B. (1986). "Instrumentalnaia systema podderzky razrabotky i otladky bolshikh program na Fortrane ES EVM" (CASE System for Development and Debugging of Large-scale FORTRAN Programs), Programming, The USSR Academy of Sciences, Moscow, 1986, No.5, pp.27-38 (in Russian).
|
|
|
Nadareishvili, G. (1975). Shakhmatnyi Etude v Gruziy (Chess Endgame in Georgia), "Sabchota Sakartvelo", Tbilisy, 1975, (in Russian).
Nadareishvili, G. (1976). Izbranyi Shakhmatnyi Etude (Selected Chess Endgame), "Fizkultura i sport", Moscow, 1976, 103 pp., 50000 copies, (in Russian).
|
|
Надареишвили Г. (1975). Шахматные этюды в Грузии, "Сабшота Сакартвело", Тбилиси, 1975.
Надареишвили Г. (1976). Избранные шахматные этюды, "Физкультура и спорт", Москва, 1976, 103 стр., 50 тыс. экз. (Харьковская книжная фабрика).
|
|
|
Narasimhan, R.N. (1966). "Syntax-Directed Interpretation of Classes of Pictures", Communications of the ACM, 1966, No.9, pp.166-173.
|
|
Нарасимхан Р.Н. (1966), "Syntax-Directed Interpretation of Classes of Pictures", Communications of the ACM, 1966, No.9, pp.166-173.
Нарасимхан Р.Н. (1969). "Лингвистический подход к распознаванию образов", в сб. Автоматический анализ сложных изображений, Перевод под ред. Э.М.Бравермана, Москва, "Мир", 1969.
|
|
|
|
|
Newell, A., Simon, H.A. (1972). Human Problem Solving, Prentice Hall, Englewood Cliffs, NJ, 1972.
(
See Also
Ed. by Feigenbaum E.A., Feldman J. (1963). Computers and Thought, A Collection of Articles, University of California at Berkeley, McGraw-Hill Book Co., New York, 1963.
)
|
|
|
|
|
Нильсон Н.Дж. (1980), Principles of Artificial Intelligence, Tioga Publ., Palo Alto, CA, 1980.
Нильсон Н. (1985). Принципы искусственного интеллекта, Москва, "Радио и связь", 1985.
(
см. также
Нильсон Н.Дж., 1973
Хант Эрл, 1978
Кузин Л.Т., 1979
Лорьер Ж.-Л., 1991
)
|
|
|
|
|
Pavlidis, T. (1972). "Linear and Context-Free Graph Grammars", Journal of the ACM, 1972, No.19, pp.11-22.
Pavlidis, T. (1977). Structural Pattern Recognition, 1977, Springer-Verlag, New York.
|
|
Павлидис Т. (1972), "Linear and Context-Free Graph Grammars", Journal of the ACM, 1972, No.19, pp.11-22.
Павлидис Т. (1977), Structural Pattern Recognition, 1977, Springer-Verlag, New York.
(
см. также
Ту Дж., Гонсалес Р., 1978
Хант Эрл, 1978
Кузин Л.Т., 1979
Павлидис Т., 1979, 1986
Русын Б.П., 1986
)
|
|
|
Pednault, E.P. (1987). "Solving Multiagent Dynamic World Problems in the Classical Planning Framework", Proc. of the 1986 Workshop "Reasoning about actions and Plans", Los Altos, CA, 1987, pp.42-82.
|
|
|
Педнаулт Э.П. (1987), "Solving Multiagent Dynamic World Problems in the Classical Planning Framework", Proc. of the 1986 Workshop "Reasoning about actions and Plans", Los Altos, CA, 1987, pp.42-82,
|
|
|
Pelavin, R., Allen, J.F. (1986). "A Formal Logic of Plans in a Temporally Rich Domain", Proc. IEEE, Spec. Issue Knowledge Representation, 1986, No.74, pp.1364-1382.
|
|
|
Пелевин Р., Аллен Дж.Ф. (1986), "A Formal Logic of Plans in a Temporally Rich Domain", Proc. IEEE, Spec. Issue Knowledge Representation, 1986, No.74, pp.1364-1382.
|
|
|
|
|
|
Polya, G. (1945). How to Solve It, Princeton University Press, Princeton, NJ, 1945.
|
|
Пойа Д. (1945), How to Solve It, Princeton University Press, Princeton, NJ, 1945.
Пойа Д. (1959). Как решать задачу, "Учпедгиз", Москва, 1957.
(
см. также
Пойа Д., 1975, 1976
Хант Эрл, 1978
Лорьер Ж.-Л., 1991
)
|
|
|
Rash, J.L. (1994). "Guest Editor's Note", Telematics and Informatics, 1994, No.11(4), pp.293.
|
|
|
Раш Дж.(1994), "Guest Editor's Note", Telematics and Informatics, 1994, No.11(4), pp.293.
|
|
|
Reznitskiy, A.I., Bordiugov, V.M., Stilman, B. (1983). "Metod planirovania remontov energooborudovania" (A Method for Planning Power Equipment Maintenance), Electrichestvo (Electricity), 1983, No.2, pp.58-61, (in Russian).
|
|
|
|
Reznitskiy, A.I., Stilman, B. (1983). "Primenenie metoda PIONEER" (Use of Method PIONEER in Automating the Planning of Maintenance of Power-Generating Equipment", Avtomatica i Telemechanika (Automatics and Telemechaniks), 1983, No.11, pp.147-153, (in Russian).
|
|
|
|
Reznitskiy, A.I. (1987). "Zametky po formalizaciy ekonomicheskogo algoritma" (Notes on Formalizing the Algorithm for Economics), Work Notes, 1987, (in Russian).
|
|
|
|
|
|
Rodin E.Y. (1988). "Semantic Control Theory", Applied Mathematics Letters, 1988, No.1(1), pp.73-78.
Rodin E.Y. (1992). Private Communication, June 1992.
Rodin E.Y. (1994). Private Communication, August 1994.
Rodin E.Y., Lirov, Y., Mittnik, S., McElhaney, B.G., Wilbur, L. (1987). "Artificial Intelligence in Air Combat Games", Computers and Mathematics with Applications, 1987, No.13(1-3), pp.261-274.
Rodin E.Y., Ghosh, B.K., Golenko, F., Weil, R. (1988). "Collision Free Path Planning in a Dynamic Environment: Semantic Control Approach", Simulation, 1988, No.11, pp.196-201.
|
|
Родин Э. (1988), "Semantic Control Theory", Applied Mathematics Letters, 1988, No.1(1), pp.73-78.
Родин Э. (1992), Private Communication, June 1992.
Родин Э. (1994)), Private Communication, August 1994.
Родин Э., Лиров Я., и др. (1987), "Artificial Intelligence in Air Combat Games", Computers and Mathematics with Applications, 1987, No.13(1-3), pp.261-274.
Родин Э., и др. (1988), "Collision Free Path Planning in a Dynamic Environment: Semantic Control Approach", Simulation, 1988, No.11, pp.196-201.
|
|
|
Rosenfeld, A. (1979). Picture Languages, Formal Models for Picture Recognition, Academic Press, 1979.
|
|
Розенфельд А. (1979), Picture Languages, Formal Models for Picture Recognition, Academic Press, 1979.
(
см. также
Розенфельд А., 1972
Ту Дж., Гонсалес Р., 1978
Хант Эрл, 1978
Шлезингер М.И., 1989
)
|
|
|
|
Розенкранц Д. (1969), "Programmed Grammars and Classes of Formal Languages", J. of the ACM, 1969, No.1, pp.107-131.
Розенкранц Д. (1970). "Программные грамматики и классы формальных языков", Сборник переводов по вопросам информационной теории и практики, Москва, ВИНИТИ, 1970, № 16.
|
|
Sacerdoti, E.D. (1974). "Planning in a Hierarchy of Abstraction Spaces", Artificial Intelligence, 1974, No.5, pp.115-135.
Sacerdoti, E.D. (1975). "The Nonlinear Nature of Plans", Proc. Int. Joint Conference on Artificial Intelligence, pp.206-214.
|
|
Сакердоти Э.Д. (1974), "Planning in a Hierarchy of Abstraction Spaces", Artificial Intelligence, 1974, No.5, pp.115-135.
Сакердоти Э.Д. (1975), "The Nonlinear Nature of Plans", Proc. Int. Joint Conference on Artificial Intelligence, pp.206-214.
|
|
|
Shannon, C.E. (1950). "Programming a digital computer for playing chess", Philosophy Magazine, March, 1950, No.41, pp.356-375.
|
|
Шеннон К. (1950), "Programming a digital computer for playing chess", Philosophy Magazine, March, 1950, No.41, pp.356-375.
Шеннон К. (1963). Работы по теории информации и кибернетике, Сборник статей, Москва, "ИЛ", 1963.
(см. также "Вычислительные машины и мышление", 1967)
|
|
|
Shaw, A.C. (1969). "A Formal Picture Description Scheme as a Basis for Picture Processing System", Information and Control, 1969, No.19, pp.9-52.
|
|
|
Шоу А. (1969), "A Formal Picture Description Scheme as a Basis for Picture Processing System", Information and Control, 1969, No.19, pp.9-52.
|
|
|
Shinar, J. (1990). "Analysis of Dynamic Conflicts by Techniques of Artificial Intelligence", INRIA Report, Antipolis.
|
|
|
Шинар Дж. (1990), "Analysis of Dynamic Conflicts by Techniques of Artificial Intelligence", INRIA Report, Antipolis.
|
|
Skhisov, E. (1997). "War Game Simulation Using Linguistic Geometry and Parallel Object Oriented Tools", M.S. Thesis, 1997, 109 pp., University of Denver.
Skhisov, E., Stilman, B. (1997). "War Game Simulation Tools Based on Linguistic Geometry Approach", Proc. of the 15th IMACS Congress on Scientific Computation, Modeling and Applied Mathematics, Berlin, Germany, Aug. 1997, pp.515-520.
Skhisov, E., Stilman, B. (1998a). "No-Search Approach in Linguistic Geometry: Experiments with Concurrent Agents", (4935-4940), (3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct. 1998, pp.11-14.
Skhisov, E., Stilman, B. (1998b). "No-Search Approach in Linguistic Geometry: Combat Simulation Tool", (4941-4945), (3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct. 1998, pp.11-14.
|
|
Скисов Э. (1997), "War Game Simulation Using Linguistic Geometry and Parallel Object Oriented Tools", M.S. Thesis, 1997, 109 pp., University of Denver.
Скисов Э., Штильман Б. (1997), "War Game Simulation Tools Based on Linguistic Geometry Approach", Proc. of the 15th IMACS Congress on Scientific Computation, Modeling and Applied Mathematics, Berlin, Germany, Aug. 1997, pp.515-520.
Скисов Э., Штильман Б. (1998a), "No-Search Approach in Linguistic Geometry: Experiments with Concurrent Agents", (4935-4940), (3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct. 1998, pp.11-14.
Скисов Э., Штильман Б. (1998b), "No-Search Approach in Linguistic Geometry: Combat Simulation Tool", (4941-4945), (3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct. 1998, pp.11-14.
|
|
|
|
Слэйгл Дж., Диксон Дж. (1969), "Experimentics with Some Programs thet Search Game Trees", Journal of the ACM, No.16(2), 1969, pp.189-207.
Слэйгл Дж., Диксон Дж. (1970), "Experimentics with the m and n Tree Searching Program", Journal of the ACM, No.17, 1970, pp.147-154.
(см. также Слэйгл Дж., 1973)
|
|
Stefik, M. (1981). "Planning and meta-planning (MOLGEN: Part 2)", Artificial Intelligence, 1981, No.2, pp.141-169.
Stefik, M. (1995). Introduction to Knowledge Systems, 3nd Ed., San Francisco, CA: Morgan Kaufmann, 1995.
|
|
Штефик М. (1981), "Planning and meta-planning (MOLGEN: Part 2)", Artificial Intelligence, 1981, No.2, pp.141-169.
Штефик М. (1995), Introduction to Knowledge Systems, 3nd Ed., San Francisco, CA: Morgan Kaufmann, 1995.
Штефик М. (2002).
Программирование на языке CLIPS
,
Введение в экспертные системы
,
Перевод с англ. в HTML с 3-го изд., 2002.
|
|
|
Stilman, B. (1975). "Formirovanie Mnozestva Puchkov Traectorii" (Generation of the Set of Trajectory Bundles), Appendix 1, pp.70-78 in Botvinnik M.M., 1975, (in Russian).
|
|
|
Stilman, B. (1976a). "Das Programmieren der Generierung und des Minimax innerhalb der Spielzonen" (Programming of Search and Minimax within a Zone), Abt, Informatik Universitat Dortmund, Dortmund, Germany, 1976, vol.29, pp.31-55, (Translated from Russian Штильман Б.М., 1976bb into German).
Stilman, B. (1976b). "Die Spielzone" (Zones), Abt, Informatik Universitat Dortmund, Dortmund, Germany, 1976, vol.29, pp.1-30, (Translated from Russian Штильман Б.М., 1976aa into German).
|
|
Штильман Б. (1976a), "Das Programmieren der Generierung und des Minimax innerhalb der Spielzonen" (Programming of Search and Minimax within a Zone), Abt, Informatik Universitat Dortmund, Dortmund, Germany, 1976, vol.29, pp.31-55, (Перевод с русского Штильман Б.М., 1976bb на немецкий).
Штильман Б. (1976b), "Die Spielzone" (Zones), Abt, Informatik Universitat Dortmund, Dortmund, Germany, 1976, vol.29, pp.1-30, (Перевод с русского Штильман Б.М., 1976aa на немецкий).
Штильман Б.М. (1976c). "Машина учится", Шахматы в СССР, 1976, № 4, стр.20-22.
|
|
|
Stilman, B. (1977). "The Computer Learns", in book Levy, D., 1976 US Computer Chess Championship, Computer Science Press, Woodland Hills, CA, 1977, pp. 83-90.
|
|
|
Штильман Б. (1977), "The Computer Learns", in book Levy, D., 1976 US Computer Chess Championship, Computer Science Press, Woodland Hills, CA, 1977, pp. 83-90.
|
|
|
Stilman, B. (1978). "Issledovanie systemy upravlenia na modely shakhmatnoi igry" (Investigation of Control System on the Model of the Game of Chess), Tech. Report, VNIIE, Moscow, 1978, 201 pp., (in Russian).
|
|
|
Штильман Б.М. (1978). "Исследование системы управления на основе модели шахматной игры", Технический отчёт, ВНИИЭ, Москва, 1978, 201 стр.
|
|
|
|
|
|
Stilman, B. (1981). "Ierarhia formalnikh grammatik dla reshenia perbornikh zadach" (Hierrachy of Formal Grammars for Solving Search Problems), Tech. Report, VNIIE, Moscow, 1981, 105 pp., (in Russian).
|
|
|
Штильман Б.М. (1981). "Иерархия формальных грамматик для решения переборных задач", Технический отчёт, ВНИИЭ, Москва, 1981, 105 стр.
|
|
|
|
|
|
|
|
|
Stilman, B. (1985a). "Ierarhia Formalnikh Grammatik dla Reshenia Perbornikh Zadach" (Hierrachy of Formal Grammars for Solving Search Problems), in Artifical Intelligence. Results und Prospects, Proc. of the Int. Workshop, Moscow, 1985, pp.63-72, (in Russian).
|
|
|
Штильман Б.М. (1985a). "Иерархия формальных грамматик для решения переборных задач", Искусственный интеллект. Итоги и перспективы. Труды международной рабочей группы, Москва, 1985, стр.63-72.
|
|
|
Stilman, B. (1985b). "Formalno-lingvisticheskaia model dlia reshenia zadach diskretnoi optimizatsii. 1. Instrumentarii formalizatsii. Yazik trajectorii" (Formal-Linguistic Model for Solving Discrete Optimization Problems. 1. Formalization Tools. Language of Trajectories), Izvestia Akademii Nauk SSSR. Tekhnicheskaia Kibernetika, Moscow, 1985, No.3, pp.110-122, (in Russian).
|
|
|
Штильман Б.М. (1985b). "Формально-лингвистическая модель для решения задач дискретной оптимизации. 1. Инструментарий формализации. Язык траекторий", Известия АН СССР. Техническая кибернетика, Москва, 1985, № 3, стр.110-122, 4886 экз.
|
|
|
Stilman, B. (1985c). "Formalno-lingvisticheskaia model dlia reshenia zadach diskretnoi optimizatsii. 2. Yazik zon, pervody, problema granits" (Formal-Linguistic Model for Solving Discrete Optimization Problems. 2. Language of Zones, Translations and Problem of Boundaries), Izvestia Akademii Nauk SSSR. Tekhnicheskaia Kibernetika, Moscow, 1985, No.4, pp.10-21, (in Russian).
|
|
|
Штильман Б.М. (1985c). "Формально-лингвистическая модель для решения задач дискретной оптимизации. 2. Язык зон, переводы и проблема границ", Известия АН СССР. Техническая кибернетика, Москва, 1985, № 4, стр.10-21, 4886 экз.
|
|
Stilman, B. (1992). "A Linguistic Geometry of Complex Systems, Abstr. 2nd Int. Symposium on Artificial Intelligence and Mathematics", Fort Lauderdale, FL, USA, Jan. 1992.
Stilman, B. (1993a).
"A Linguistic Approach to Geometric Reasoning"
, Int. J. Computers and Mathematics with Applications, 1993, No.26(7), pp.29-57.
Stilman, B. (1993b).
"Network Languages for Complex Systems"
, Int. J. Computers and Mathematics with Applications, 1993, No.26(8), pp.51-79.
Stilman, B. (1993c). "Syntactic Hierarchy for Robotic Systems", Integrated Computer-Aided Engineering, 1993, No.1(1), pp.57-81.
Stilman, B. (1993d). "A Formal Language for Hierarchical Systems Control", Languages of Design, 1993, No.1(4), pp.333-356.
Stilman, B. (1994a).
"A Linguistic Geometry of the Chess Model"
, Advances in Computer Chess 7, University of Limburg, Maastricht, Netherlands, 1994, pp.91-117.
Stilman, B. (1994b).
"A Linguistic Geometry for Space Applications"
, Proc. of 1994 Goddard Conference on Space Applications of Artificial Intelligence, NASA Goddard Space Flight Center, Greenbelt, MD, May 1995, pp.87-101.
Stilman, B. (1994c). "Heuristic Networks for Space Exploration", Telematics and Informatics, An Int. Journal on Telecommunications & Information Technology, 1994, No.11(4), pp.403-428.
Stilman, B. (1994d).
"Translations of Network Languages"
, Int. J. Computers and Mathematics with Applications, 1994, No.27(2), pp.65-98.
Stilman, B. (1994e). "A Linguistic Geometry for Control Systems Design", International Journal of Computers and Their Applications, Dec. 1994, vol. 1, No.2, pp.89-110.
Stilman, B. (1994f),
"Software Development Environment for Concurrent Design and maintenance of Complex research Projects"
, Proc. of the Int. Symposium on Applied Corporate Computing - ISACC'94, Monterrey, Mexico, Oct. 1994, pp.147-156.
Stilman, B. (1995).
"Heuristic Networks for Aerospace Systems Control: Totally Concurrent Motions"
, 1995.
Stilman, B. (1995aa).
"Multiagent Air Combat with Concurrent Motions"
, (Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.855-867.
Stilman, B. (1995a).
"Deep Search in Linguistic Geometry"
, (Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.868-879.
Stilman, B. (1995b).
"A Linguistic Geometry for 3D Strategic Planning"
, Proc. of the 1995 Goddard Conference on Space Applications of Artificial Intelligence and Emerging Information Technologies, NASA Goddard Space Flight Center, Greebelt, MD, USA, May 1995, pp.279-295.
Stilman, B. (1995c). "A Linguistic Geometry for Multiagent Systems", Proc. of The 8th Int. Conference on Industrial & Engineering Applications of Artificial Intelligence & Expert Systems - IEA/AIE, Melbourne, Australia, June 1995, pp.3-12.
Stilman, B. (1995d). "Total Concurrency and Uncertainty in Linguistic Geometry", Proc. of The IEEE Int. Symposium on Intelligent Control, Monterey, CA, USA, August 1995, pp.79-84.
|
|
Штильман Б. (1992), "A Linguistic Geometry of Complex Systems, Abstr. 2nd Int. Symposium on Artificial Intelligence and Mathematics", Fort Lauderdale, FL, USA, Jan. 1992.
Штильман Б. (1993a),
"A Linguistic Approach to Geometric Reasoning"
,
Int. J. Computers and Mathematics with Applications, 1993, No.26(7), pp.29-57.
Штильман Б. (1993b),
"Network Languages for Complex Systems"
,
Int. J. Computers and Mathematics with Applications, 1993, No.26(8), pp.51-79.
Штильман Б. (1993c), "Syntactic Hierarchy for Robotic Systems", Integrated Computer-Aided Engineering, 1993, No.1(1), pp.57-81.
Штильман Б. (1993d), "A Formal Language for Hierarchical Systems Control", Languages of Design, 1993, No.1(4), pp.333-356.
Штильман Б. (1994a),
"A Linguistic Geometry of the Chess Model"
,
Advances in Computer Chess 7, University of Limburg, Maastricht, Netherlands, 1994, pp.91-117.
Штильман Б. (1994b),
"A Linguistic Geometry for Space Applications"
,
Proc. of 1994 Goddard Conference on Space Applications of Artificial Intelligence, NASA Goddard Space Flight Center, Greenbelt, MD, May 1995, pp.87-101.
Штильман Б. (1994c), "Heuristic Networks for Space Exploration", Telematics and Informatics, An Int. Journal on Telecommunications & Information Technology, 1994, No.11(4), pp.403-428.
Штильман Б. (1994d),
"Translations of Network Languages"
,
Int. J. Computers and Mathematics with Applications, 1994, No.27(2), pp.65-98.
Штильман Б. (1994e), "A Linguistic Geometry for Control Systems Design", International Journal of Computers and Their Applications, Dec. 1994, vol. 1, No.2, pp.89-110.
Штильман Б. (1994f),
"Software Development Environment for Concurrent Design and maintenance of Complex research Projects"
,
Proc. of the Int. Symposium on Applied Corporate Computing - ISACC'94, Monterrey, Mexico, Oct. 1994, pp.147-156.
Штильман Б. (1995),
"Heuristic Networks for Aerospace Systems Control: Totally Concurrent Motions"
,
1995.
Штильман Б. (1995aa),
"Multiagent Air Combat with Concurrent Motions"
,
(Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.855-867.
Штильман Б. (1995a),
"Deep Search in Linguistic Geometry"
,
(Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.868-879.
Штильман Б. (1995b),
"A Linguistic Geometry for 3D Strategic Planning"
,
Proc. of the 1995 Goddard Conference on Space Applications of Artificial Intelligence and Emerging Information Technologies, NASA Goddard Space Flight Center, Greebelt, MD, USA, May 1995, pp.279-295.
Штильман Б. (1995c), "A Linguistic Geometry for Multiagent Systems", Proc. of The 8th Int. Conference on Industrial & Engineering Applications of Artificial Intelligence & Expert Systems - IEA/AIE, Melbourne, Australia, June 1995, pp.3-12.
Штильман Б. (1995d), "Total Concurrency and Uncertainty in Linguistic Geometry", Proc. of The IEEE Int. Symposium on Intelligent Control, Monterey, CA, USA, August 1995, pp.79-84.
|
|
Stilman, B. (1992). "A Linguistic Geometry of Complex Systems, Abstr. 2nd Int. Symposium on Artificial Intelligence and Mathematics", Fort Lauderdale, FL, USA, Jan. 1992.
Stilman, B. (1993a).
"A Linguistic Approach to Geometric Reasoning"
, Int. J. Computers and Mathematics with Applications, 1993, No.26(7), pp.29-57.
Stilman, B. (1993b).
"Network Languages for Complex Systems"
, Int. J. Computers and Mathematics with Applications, 1993, No.26(8), pp.51-79.
Stilman, B. (1993c). "Syntactic Hierarchy for Robotic Systems", Integrated Computer-Aided Engineering, 1993, No.1(1), pp.57-81.
Stilman, B. (1993d). "A Formal Language for Hierarchical Systems Control", Languages of Design, 1993, No.1(4), pp.333-356.
Stilman, B. (1994a).
"A Linguistic Geometry of the Chess Model"
, Advances in Computer Chess 7, University of Limburg, Maastricht, Netherlands, 1994, pp.91-117.
Stilman, B. (1994b).
"A Linguistic Geometry for Space Applications"
, Proc. of 1994 Goddard Conference on Space Applications of Artificial Intelligence, NASA Goddard Space Flight Center, Greenbelt, MD, May 1995, pp.87-101.
Stilman, B. (1994c). "Heuristic Networks for Space Exploration", Telematics and Informatics, An Int. Journal on Telecommunications & Information Technology, 1994, No.11(4), pp.403-428.
Stilman, B. (1994d).
"Translations of Network Languages"
, Int. J. Computers and Mathematics with Applications, 1994, No.27(2), pp.65-98.
Stilman, B. (1994e). "A Linguistic Geometry for Control Systems Design", International Journal of Computers and Their Applications, Dec. 1994, vol. 1, No.2, pp.89-110.
Stilman, B. (1994f),
"Software Development Environment for Concurrent Design and maintenance of Complex research Projects"
, Proc. of the Int. Symposium on Applied Corporate Computing - ISACC'94, Monterrey, Mexico, Oct. 1994, pp.147-156.
Stilman, B. (1995).
"Heuristic Networks for Aerospace Systems Control: Totally Concurrent Motions"
, 1995.
Stilman, B. (1995aa).
"Multiagent Air Combat with Concurrent Motions"
, (Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.855-867.
Stilman, B. (1995a).
"Deep Search in Linguistic Geometry"
, (Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.868-879.
Stilman, B. (1995b).
"A Linguistic Geometry for 3D Strategic Planning"
, Proc. of the 1995 Goddard Conference on Space Applications of Artificial Intelligence and Emerging Information Technologies, NASA Goddard Space Flight Center, Greebelt, MD, USA, May 1995, pp.279-295.
Stilman, B. (1995c). "A Linguistic Geometry for Multiagent Systems", Proc. of The 8th Int. Conference on Industrial & Engineering Applications of Artificial Intelligence & Expert Systems - IEA/AIE, Melbourne, Australia, June 1995, pp.3-12.
Stilman, B. (1995d). "Total Concurrency and Uncertainty in Linguistic Geometry", Proc. of The IEEE Int. Symposium on Intelligent Control, Monterey, CA, USA, August 1995, pp.79-84.
Stilman, B., Dyer, D. (1995e). "Linguistic Geometry for Aerospace Combat Simulation: Serial and Concurrent Agents", Proc. of the Fifth Int. Conf. on Human-Machine Interaction and Artificial Intelligence in Aerospace, Toulouse, France, Sept. 1995, pp.27-29.
|
|
Штильман Б. (1992), "A Linguistic Geometry of Complex Systems, Abstr. 2nd Int. Symposium on Artificial Intelligence and Mathematics", Fort Lauderdale, FL, USA, Jan. 1992.
Штильман Б. (1993a),
"A Linguistic Approach to Geometric Reasoning"
,
Int. J. Computers and Mathematics with Applications, 1993, No.26(7), pp.29-57.
Штильман Б. (1993b),
"Network Languages for Complex Systems"
,
Int. J. Computers and Mathematics with Applications, 1993, No.26(8), pp.51-79.
Штильман Б. (1993c), "Syntactic Hierarchy for Robotic Systems", Integrated Computer-Aided Engineering, 1993, No.1(1), pp.57-81.
Штильман Б. (1993d), "A Formal Language for Hierarchical Systems Control", Languages of Design, 1993, No.1(4), pp.333-356.
Штильман Б. (1994a),
"A Linguistic Geometry of the Chess Model"
,
Advances in Computer Chess 7, University of Limburg, Maastricht, Netherlands, 1994, pp.91-117.
Штильман Б. (1994b),
"A Linguistic Geometry for Space Applications"
,
Proc. of 1994 Goddard Conference on Space Applications of Artificial Intelligence, NASA Goddard Space Flight Center, Greenbelt, MD, May 1995, pp.87-101.
Штильман Б. (1994c), "Heuristic Networks for Space Exploration", Telematics and Informatics, An Int. Journal on Telecommunications & Information Technology, 1994, No.11(4), pp.403-428.
Штильман Б. (1994d),
"Translations of Network Languages"
,
Int. J. Computers and Mathematics with Applications, 1994, No.27(2), pp.65-98.
Штильман Б. (1994e), "A Linguistic Geometry for Control Systems Design", International Journal of Computers and Their Applications, Dec. 1994, vol. 1, No.2, pp.89-110.
Штильман Б. (1994f),
"Software Development Environment for Concurrent Design and maintenance of Complex research Projects"
,
Proc. of the Int. Symposium on Applied Corporate Computing - ISACC'94, Monterrey, Mexico, Oct. 1994, pp.147-156.
Штильман Б. (1995),
"Heuristic Networks for Aerospace Systems Control: Totally Concurrent Motions"
,
1995.
Штильман Б. (1995aa),
"Multiagent Air Combat with Concurrent Motions"
,
(Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.855-867.
Штильман Б. (1995a),
"Deep Search in Linguistic Geometry"
,
(Symposium on LINGUISTIC GEOMETRY AND SEMANTIC CONTROL), Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.868-879.
Штильман Б. (1995b),
"A Linguistic Geometry for 3D Strategic Planning"
,
Proc. of the 1995 Goddard Conference on Space Applications of Artificial Intelligence and Emerging Information Technologies, NASA Goddard Space Flight Center, Greebelt, MD, USA, May 1995, pp.279-295.
Штильман Б. (1995c), "A Linguistic Geometry for Multiagent Systems", Proc. of The 8th Int. Conference on Industrial & Engineering Applications of Artificial Intelligence & Expert Systems - IEA/AIE, Melbourne, Australia, June 1995, pp.3-12.
Штильман Б. (1995d), "Total Concurrency and Uncertainty in Linguistic Geometry", Proc. of The IEEE Int. Symposium on Intelligent Control, Monterey, CA, USA, August 1995, pp.79-84.
Штильман Б., Дир Д. (1995e), "Linguistic Geometry for Aerospace Combat Simulation: Serial and Concurrent Agents", Proc. of the Fifth Int. Conf. on Human-Machine Interaction and Artificial Intelligence in Aerospace, Toulouse, France, Sept. 1995, pp.27-29.
|
|
|
|
|
|
Stilman, B. (1996b). "Linguistic Geometry Tools Generate Optimal Solutions", Conceptual Structure: Knowledge Representation as Interlingua, Proc. of the 4th Int. Conf. on Conceptual Structures, ICCS'96, Sydney, Australia, August 1996, pp.75-99; pub.. as "Lecture Notes", in Artificial Intelligence, No. 1115, Springer-Verlag, Berlin, 1996.
|
|
|
Штильман Б. (1996b), "Linguistic Geometry Tools Generate Optimal Solutions", Conceptual Structure: Knowledge Representation as Interlingua, Proc. of the 4th Int. Conf. on Conceptual Structures, ICCS'96, Sydney, Australia, August 1996, pp.75-99; pub.. as "Lecture Notes", in Artificial Intelligence, No. 1115, Springer-Verlag, Berlin, 1996.
|
|
|
|
|
Stilman, B. (1997b). "From Serial to Concurrent Motions in Multiagent Systems: A Linguistic Geometry Approach", Journal of Systems Engineering, 1997, (to appear).
Stilman, B. (1997c). "Fighting Dimensionality with Linguistic Geometry: Serial and Concurrent Strategies", in the book Computer-Intensive Dimensioality, Ed. Warwick, K., Karny, M.; Birkhauser Publ., Boston, 1997, pp.1-47.
Stilman, B. (1997d). "Managing Search Complexity in Linguistic Geometry", IEEE Transactions on Systems, Man, and Cybernetics, Dec. 1997, vol. 27, No.6, pp.978-998.
Stilman, B. (1998a). "No-Search Approach in Linguistic Geometry: State Space Chart", (The 3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct.11-14, 1998, pp.4907-4912.
Stilman, B. (1998b). "No-Search Approach in Linguistic Geometry: Constructions of Strategies", (The 3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct.11-14, 1998, pp.4913-4918.
Stilman, B. (1998c). "Solving Games by Construction of Strategies", Notes of the CTS Workshop on Combinatorics and Algorithms, Taipei, Taiwan, Dec.21-23, 1998, pp.74-101.
Stilman, B. (1998d). "Introductions to Linguistic Geometry Tools: Selected Topics", (The 3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct.11-14, 1998, pp.3183-3188.
|
|
Штильман Б. (1997b), "From Serial to Concurrent Motions in Multiagent Systems: A Linguistic Geometry Approach", Journal of Systems Engineering, 1997, (to appear).
Штильман Б. (1997c), "Fighting Dimensionality with Linguistic Geometry: Serial and Concurrent Strategies", in the book Computer-Intensive Dimensioality, Ed. Warwick, K., Karny, M.; Birkhauser Publ., Boston, 1997, pp.1-47.
Штильман Б. (1997d), "Managing Search Complexity in Linguistic Geometry", IEEE Transactions on Systems, Man, and Cybernetics, Dec. 1997, vol. 27, No.6, pp.978-998.
Штильман Б. (1998a), "No-Search Approach in Linguistic Geometry: State Space Chart", (The 3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct.11-14, 1998, pp.4907-4912.
Штильман Б. (1998b), "No-Search Approach in Linguistic Geometry: Constructions of Strategies", (The 3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct.11-14, 1998, pp.4913-4918.
Штильман Б. (1998c), "Solving Games by Construction of Strategies", Notes of the CTS Workshop on Combinatorics and Algorithms, Taipei, Taiwan, Dec.21-23, 1998, pp.74-101.
Штильман Б. (1998d), "Introductions to Linguistic Geometry Tools: Selected Topics", (The 3d Symposium on Linguistic Geometry), Proc. of the IEEE International Conference on Systems, Man, and Cybernetics - SMC'98, San Diego, CA, USA, Oct.11-14, 1998, pp.3183-3188.
|
|
|
|
|
Штильман Борис, (2000),
"Лингвистическая Геометрия: от Перебора к Построению"
,
"Linguistic Geometry: From Search to Construction", Series: Operations Research/Computer Science Interfaces Series, Vol. 13, 2000, 416p., Hardcover, ISBN: 0-7923-7738-9, © Springer.
Part of Springer Science+Business Media
|
|
Stilman, B., Fletcher, C., (1998). "Systems Modeling in Linguistic Geometry: Natural and Artificial Conflicts", Int. J. Systems Analysis, Modeling, Simulation, May 1998, pp.1-42.
Stilman, M., Yakhnis, V., (1998). "Linguistic Geometry Tools for Multiple Agents with Variable Speeds", Proc. of the IEEE International Conference on Systems, Man, and Cybernetics, La Jolla, CA, Oct. 1998.
|
|
Штильман Б., Флечер К., (1998), "Systems Modeling in Linguistic Geometry: Natural and Artificial Conflicts", Int. J. Systems Analysis, Modeling, Simulation, May 1998, pp.1-42.
Штильман М., Яхнис В., (1998), "Linguistic Geometry Tools for Multiple Agents with Variable Speeds", Proc. of the IEEE International Conference on Systems, Man, and Cybernetics, La Jolla, CA, Oct. 1998.
|
|
|
|
|
|
Tate, A., Hendler, J., Drummond, M., (1990). "A Review of AI Planning Techiques", in Readings in Planning, San Mateo, CA: Morgan Kaufmann, 1995, pp.26-49.
|
|
|
Turek, R. (1996). "The Application of Linguistic Geometry to the Routing of Emergency Vehicles", M.S. Thesis, University of Colorado at Denver, 1996, 44 pp.
Turek, R. (1997). "The Application of Linguistic Geometry to the Routing of Emergency Vehicles", Advances in Systems Science and Applications, Jan 1997, pp.186-195, (special issue).
|
|
Тюрек Р. (1996), "The Application of Linguistic Geometry to the Routing of Emergency Vehicles", M.S. Thesis, University of Colorado at Denver, 1996, 44 pp.
Тюрек Р. (1997), "The Application of Linguistic Geometry to the Routing of Emergency Vehicles", Advances in Systems Science and Applications, Jan 1997, pp.186-195, (special issue).
|
|
|
Volchenkov, N.G. (1979). "Interpretator beskontestnikh upravliaemikh parametricheskikh programmnikh grammatik" (The Interpreter of Context-Free Controlled Parameter Programmed Grammars), in Voprosy Kibernetiky: Intellektualnie banky dannikh (Proceedings on Cybernetics: Intelligent Data Banks), L.T. Kuzin, Eds., The USSR Academy of Sciences, Scientific Board on Complex Problem «Cybernetics», Moscow, pp. 147-157, (in Russian).
|
|
|
Волченков Н.Г. (1979). "Интерпретатор бесконтекстных управляемых параметрических программных грамматик", в сб. Вопросы кибернетики. Интеллектуальные банки данных, Под ред. Л.Т.Кузина, Москва, Науч. совет по компл. пробл. «Кибернетика» АН СССР, 1979, стр.147-157.
|
|
|
|
Фон Нейман Дж., Моргенштерн O. (1944), Theory of Games and Economic Behavior, Princeton University Press, 1944.
Фон Нейман Дж., Моргенштерн O. (1970). Теория игр и экономическое поведение, Москва, "Наука", 1970.
(
см. также
Фон Нейман Дж., 1961
Кузин Л.Т., 1979
)
|
|
|
Wood, D. (1996). "BGF: A Framework for Board Game Applets", M.S. Thesis, University of Colorado at Denver, 1996, 120 pp.
|
|
|
Вуд Д. (1996), "BGF: A Framework for Board Game Applets", M.S. Thesis, University of Colorado at Denver, 1996, 120 pp.
|
|
Yakhnis, A. (1997a). "Refinement of Strategies within Multi-agent Strategic Approach and Linguistic Geometry", Advances in Systems Science and Applications, Jan 1997, pp.173-177, (special issue).
Yakhnis, A., Yakhnis, V. (1990). "Extension of Gurevich-Harrington's restricted Memory determinacy Theorem: A Criterion for the Winning Player and an Explicit Class of Winning Strategies", Annals of Pure and Applied Logic, 1990, vol.48, pp.277-297.
Yakhnis, A., Yakhnis, V. (1993). "Gurevich-Harrington's Games defined by Finite Automata", Annals of Pure and Applied Logic, 1993, vol.62, pp.265-294.
Yakhnis, A., Yakhnis, V., Stilman, B. (1997). "Linguistic Geometry and Board Game Approach to Automated Generation of Schedules", Proc. of the 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Germany, Aug. 1997, pp.485-490.
|
|
Яхнис А. (1997a), "Refinement of Strategies within Multi-agent Strategic Approach and Linguistic Geometry", Advances in Systems Science and Applications, Jan 1997, pp.173-177, (special issue).
Яхнис А., Яхнис В. (1990), "Extension of Gurevich-Harrington's restricted Memory determinacy Theorem: A Criterion for the Winning Player and an Explicit Class of Winning Strategies", Annals of Pure and Applied Logic, 1990, vol.48, pp.277-297.
Яхнис А., Яхнис В. (1993), "Gurevich-Harrington's Games defined by Finite Automata", Annals of Pure and Applied Logic, 1993, vol.62, pp.265-294.
Яхнис А., Яхнис В., Штильман Б. (1997), "Linguistic Geometry and Board Game Approach to Automated Generation of Schedules", Proc. of the 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Germany, Aug. 1997, pp.485-490.
|
|
Yakhnis, V. (1998). "Grammar of Zones with Admissible Trajectories of Arbitrary Degrees", Proc. of the IEEE Int. Conf. on Systems, Man, and Cybernetics, La Jolla, CA, Oct. 1998.
Yakhnis, V., Stilman, B. (1995a).
"Foundations of Linguistic Geometry: Complex Systems and Winning Conditions"
, Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.843-854.
Yakhnis, V., Stilman, B. (1995b).
"A Multi-Agent Graph-Game Approach to Theoretical Foundations of Linguistic Geometry"
, Proc. of the Second World Conference on the Fundamentals of Artificial Intelligence (WOCFAI'95), Paris, France, July 1995.
Yakhnis, V., Yakhnis, A., Stilman, B. (1996). "Managing Large System State Spaces via Linguistic Geometry (LG) Trajectories", Proc. of the Int. Conf. Inelligent Systems: Simeotic Perspective, Gaithersburg, MD, Oct. 1996, pp.284-290.
Yakhnis, V., Yakhnis, A., Stilman, B. (1997). "A Linguistic Geometry Grammar of Admissible Trajectories of Arbitrary Degrees", Proc. of the 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Germany, Aug. 1997, pp.509-514.
|
|
Яхнис В. (1998), "Grammar of Zones with Admissible Trajectories of Arbitrary Degrees", Proc. of the IEEE Int. Conf. on Systems, Man, and Cybernetics, La Jolla, CA, Oct. 1998.
Яхнис В., Штильман Б. (1995a),
"Foundations of Linguistic Geometry: Complex Systems and Winning Conditions"
,
Proc. of the First World Congress on Intelligent Manufacturing: Processes and Systems, Mayaguez, Puerto Rico, Feb. 1995, pp.843-854.
Яхнис В., Штильман Б. (1995b),
"A Multi-Agent Graph-Game Approach to Theoretical Foundations of Linguistic Geometry"
,
Proc. of the Second World Conference on the Fundamentals of Artificial Intelligence (WOCFAI'95), Paris, France, July 1995.
Яхнис В., Яхнис А., Штильман Б. (1996), "Managing Large System State Spaces via Linguistic Geometry (LG) Trajectories", Proc. of the Int. Conf. Inelligent Systems: Simeotic Perspective, Gaithersburg, MD, Oct. 1996, pp.284-290.
Яхнис В., Яхнис А., Штильман Б. (1997), "A Linguistic Geometry Grammar of Admissible Trajectories of Arbitrary Degrees", Proc. of the 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics, Berlin, Germany, Aug. 1997, pp.509-514.
|
|
|
Yudin, A.D. (1984). "The endgame Library in PIONEER (Using Historical Experience by the Handbok Method and the Outreach Method), Appendix 3, pp.110-133 in Botvinnik M.M., 1984
|
|
Юдин А.Д. (1979). "Библиотека эндшпиля программы ПИОНЕР (использование опыта прошлого по справочному методу и методу стремления)", Приложение 3, стр.110-133 в кн. Ботвинник М.М., 1979.
(
см. также
Юдин А.Д., 1975, 1975a, 1976
Резницкий Ф.И., Юдин А.Д., 1979
)
|
|
|
Zeitman S.(1994). "Unforgettable forgetful determinacy", Logic and Computation, 1994, vol.4, pp.273-283.
|
|
|
Зейтман С. (1994), "Unforgettable forgetful determinacy", Logic and Computation, 1994, vol.4, pp.273-283.
|
|