|
◄ БЛАГОДАРНОСТИ
▲ Выше
Глава 1.1 ►
|
| 1 ВВЕДЕНИЕ |
|
Лингвистическая Геометрия (LG) включает синтаксические инструменты для представления знаний и логического вывода в многоагентных системах, путём моделирования их как абстрактные настольные игры. Инструменты LG позволяют оценить вычислительную сложность и точность решений, а также сгенерировать компьютерные программы для определенных проблемных областей. LG позволяет нам выявить внутренние, скрытые свойства эвристик человека-эксперта, которые продемонстрировали успех в некотором классе игр. Этот подход даёт возможность переносить формальные утверждения и конструкции от одной задачи к другой, т.е. повторно использовать инструменты в новой проблемной области. В некотором смысле, подход на основе LG — это применение метода шахматного эксперта к управлению навигацией робота или календарному планированию ремонтов и наоборот. Что мы знаем о методах шахматного эксперта? Конечно, компьютер — это совершенный инструмент для распознавания и моделирования таких методов. История компьютерных шахмат началась со статьи профессора Клода Шеннона (1950), в которой он предложил общую схему для последующих разработок. Используя, главным образом, поиск решения по методу полного перебора (англ. «брут форс» — грубая сила), т.е. полагаясь, в конечном счёте, на быстродействие компьютеров, шахматные программы постепенно улучшили свой уровень игры (Ньюборн, 1996). В середине 90-х годов, они достигли уровня гроссмейстера. После исторического события в мае 1997 года, когда Дип Блю (Deep Blue — компьютерная шахматная система фирмы IBM) победила чемпиона мира по шахматам Гарри Каспарова, компьютерные шахматы потеряли свою захватывающую привлекательность. В июне 1997 года, профессор Джон Маккарти писал: “В 1965 году российский математик Александр Кронрод сказал, что «шахматы — дрозофила ИИ». Однако компьютерные шахматы разрабатывались так, как могло бы случиться с генетикой, если бы усилия учёных концентрировались, начиная с 1910 года, только на выведении быстрой дрозофилы. Но тогда мы всё же имели бы немного науки, хотя главным образом, мы получили бы очень быстрых плодовых мушек” (Маккарти, 1997). Все самые большие успехи в компьютерных шахматах, включая триумф Дип Блю, были связаны с методом решения «брут форс». Сможем ли мы использовать какие-либо из этих результатов для решения других задач, особенно для задач, имеющих намного большую размерность? Вряд ли. Даже на суперкомпьютерах будущего, мы не сможем решать такие задачи по методу «брут форс». Метод гроссмейстера (т.е. почти без перебора ходов) пока ещё не раскрыт. После события 1997 года стало яснее, чем когда-либо прежде, что шахматы предназначены быть научной дрозофилой ИИ, а не только тестом для проверки скорости компьютеров (Маккарти, 1990, 1997). Однако, не все исследования в компьютерных шахматах проводились в направлении поиска решений по методу «брут форс». В 70-х и 80-х годах в Москве (Россия) разрабатывался проект ПИОНЕР во главе с экс-чемпионом мира по шахматам профессором Михаилом Ботвинником. В своей книге (1984) Ботвинник писал, что метод решения «брут форс» “едва ли способен к дальнейшему прогрессу. Настала очередь принять компьютеру более плодотворный метод, возможно, ПИОНЕР. И, если ПИОНЕР неудачен, то мы должны быть уверены, что другой метод всё же будет найден. Задача должна быть и будет решена”. LG — прямой преемник проекта ПИОНЕР. Дрозофила ИИ “летит через эту книгу, оплодотворяя различные эксперименты и генерируя новые идеи”. Среди других примеров в этой книге мы рассматриваем ряд задач моделирования боя. Это — Рети-подобные задачи, т.е. обобщения знаменитого этюда Рети (Ботвинник, 1979, 1984). Здесь они — называются задачами 2D/4A, 3D/4A, с частично и полностью параллельным моделированием боя. Эти задачи достаточно просты, чтобы использоваться для демонстрации LG-подхода. С другой стороны, они всё-таки не тривиальны и требуют существенного перебора, если их решать с использованием традиционных подходов. Важно общее понимание того, что Рети-подобные задачи являются P-SPACE-полными или, по крайней мере, относятся к группе (или подклассу), так называемых, NP-сложных задач, т.е. таких, для которых не существует алгоритмов, приводящих к решению за полиномиальное время (Гэри и Джонсон, 1991). Инструменты LG позволяют нам решать задачи из этого подкласса и многие другие задачи, используя алгоритмы полиномиальной сложности. Поэтому можно предположить, что Рети-подобные задачи являются представителями более широкого класса задач с низкой (полиномиальной) вычислительной сложностью (т.е. их можно рассматривать и как новый подкласс в группе P-TIME задач). Вероятно, многие важные задачи из реальной жизни, рассмотренные ниже, входят в этот подкласс (Рети-подобных задач). |
|
|
|
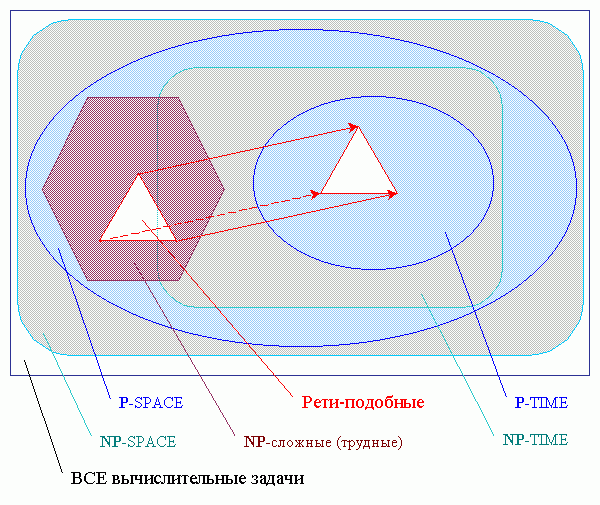
Различают классы задач полиномиальной сложности по времени:
P-TIME ⊆ NP-TIME ,
NP-полные=NP-сложные ∩ NP-TIME
и по требуемой памяти:
NP-сложные ⊆
P-SPACE ⊆
NP-SPACE ,
где P - детерминированная полиномиальная сложность,
а NP - недетерминированная полиномиальная сложность.
Упрощённая классификация задач по вычислительной сложности.
|
|
◄ БЛАГОДАРНОСТИ ▲ В начало текущей Глава 1.1 ► |
|
Последнее обновление 09.09.2005, size=12 294 bytes
© 2005 г., Александр Тимофеев, г.Харьков, Украина, Об авторе eMail: atimopheyev@yahoo.com |