|
▲ Top
▼ Table of Contents
▲ in Russian (по рус.)
▲ References
▲ Chess EndGames
|
|
Linguistic Geometry
From Search to Construction Boris Stilman University of Colorado at Denver & STILMAN Advanced Strategies, LLC Kluwer Academic Publishers Boston Dordrecht London |
|
|

To order this book contact
Kluwer Academic Publishers at http://www.wkap.nl/series.htm/ORCS http://www.stilman-strategies.com/bstilman/research/BOOKpdfs/LG01.pdf |
|
|
|
Copyright © 1999 Boris Stilman. All rights reserved. No part of this publication may be reproduced, stored in a database retrieval system, distributed, or transmitted, in any form or by any other means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of Boris Stilman. |
|
|
|
TABLE OF CONTENTS
Titul page PREFACE ACKNOWLEDGMENTS 1. Introduction...........................................................1 1.1 Problems..............................................................2 1.2 Current Approaches....................................................4 1.3 LG Approach at a Glance...............................................9 1.4 LG Approach: Deeper Account..........................................13 1.5 LG Strategies and Game Theory........................................19 1.6 LG: Three Stages of Development......................................22 1.7 Stage One: Project PIONEER...........................................24 1.8 Stage Two: Mathematical Tools........................................28 1.9 Stage Three: Modern History..........................................32 2. Hierarchy of Formal Languages.........................................39 2.1 Hierarchy Outline....................................................39 2.2 Class of Problems....................................................40 2.3 Various Problems as Complex Systems..................................45 2.4 Set of Paths: Language of Trajectories...............................50 2.5 Board and State Distances............................................52 2.6 Networks of Paths: Languages of Networks.............................54 2.7 Representation of Movement: Translations.............................66 2.8 Search by Construction: Languages of Searches........................71 2.9 Historical Remarks...................................................75 3. Robot Combat for 2D District..........................................77 3.1 Problem Statement....................................................77 3.2 LG Search............................................................79 3.3 Discussion...........................................................88 3.4 Historical Remarks...................................................89 4. Expanding to 3D Space.................................................91 4.1 3D/4A Robot Combat...................................................91 4.2 LG Search within Insufficient Horizon................................94 4.3 LG Search within Horizon 5...........................................98 4.4 From 2D to 3D: Running Time Change..................................105 4.5 Historical Remarks..................................................106 5. Deeper Search, More Agents...........................................107 5.1 2D/8A Air Combat....................................................107 5.2 Deep Search for Air Combat..........................................112 5.3 3D/8A Space Combat..................................................128 5.4 A New Level of Sophistication: Preliminary Conclusions..............131 5.5 Historical Remarks..................................................134 6. Concurrency, n×n District............................................137 6.1 Serial Mode Relaxation: Partial Concurrency.........................137 6.2 LG Search for Problem with Partial Concurrency......................139 6.3 Second Problem with Partial Concurrency.............................143 6.4 Second Problem: LG Search...........................................145 6.5 Problem with Total Concurrency and n×n District.....................150 6.6 Problem with Total Concurrency: LG Search...........................155 6.7 Impact of Concurrency...............................................160 6.8 Historical Remarks..................................................162 7. Scheduling: Artificial Conflict......................................165 7.1 Problem Statement...................................................165 7.2 Conversion into Two-Player Game.....................................168 7.3 Scheduling: Search and Solution.....................................172 7.4 Formal Representation...............................................174 7.5 Evaluation and Implementation.......................................177 7.6 Applicability of LG.................................................178 8. Generating Techniques................................................181 8.1 Chomsky Grammars....................................................181 8.2 Controlled Grammars: Introduction...................................183 8.3 Tower of Hanoi: 3 Discs.............................................184 8.4 Tower of Hanoi: n Discs.............................................186 8.5 Controlled Grammars: Formal Definition..............................188 8.6 Historical Remarks..................................................191 9. Language of Trajectories.............................................193 9.1 Shortest Trajectories: Generating Grammar...........................193 9.2 Generation of Shortest 2D Trajectories..............................196 9.3 Generation of Shortest 3D Trajectories..............................200 9.4 Shortest Trajectories: Correctness and Completeness.................204 9.5 Admissible Trajectories: Generating Grammar.........................207 9.6 Avoiding Obstacles: Generation of Admissible Trajectories...........210 9.7 Admissible Trajectories: Correctness and Completeness...............215 9.8 Trajectories for the Game of Chess..................................219 9.9 Trajectories for Scheduling.........................................224 9.10 Trajectories for Agents with Variable Speed........................226 9.11 Language of Trajectories: Efficient Implementation.................232 9.12 Historical Remarks.................................................233 10. Language of Zones...................................................235 10.1 Grammar of Zones...................................................235 10.2 Generation of Zones................................................238 10.3 Geometry of Zones..................................................250 10.4 Zones for the Game of Chess........................................253 10.5 Zones for Scheduling...............................................254 10.6 Historical Remarks.................................................256 11. Translations........................................................259 11.1 Approaching a Solution of the Problem of Change....................259 11.2 Theorem about Translations.........................................265 11.3 Search with Translations...........................................278 11.4 Translations and Freeze............................................284 11.5 Historical Remarks.................................................286 12. Languages of Searches...............................................287 12.1 General Searches...................................................287 12.2 Reduced Searches...................................................290 12.3 Grammar of Translations............................................294 12.4 Quality of Trajectories and Zones..................................297 12.5 Tree Inspection Procedure..........................................300 12.6 Historical Remarks.................................................303 13. From Search to Construction.........................................305 13.1 Problem Statement..................................................305 13.2 Algorithm Outline..................................................306 13.3 Preliminary Definitions............................................307 13.4 Terminal Sets Expansion............................................308 13.5 Structure of Expanded Terminal Sets................................311 13.6 State Space Chart..................................................319 13.7 Outline of Potential Strategies....................................323 13.8 Construction of Strategy at the Start State........................330 13.9 Strategies for Reti-like problems..................................335 13.10 Discussion........................................................337 13.11 Historical Remarks................................................339 14. Computational Complexity............................................341 14.1 Running Time: Conventional Algorithms for Reti-like problems.......341 14.2 Running Time: Grammar of Shortest Trajectories.....................347 14.3 Running Time: Grammar of Zones.....................................350 14.4 Running Time: Unfolding Bundles of Trajectories and Cloning Zones..353 14.5 Computational Complexity: Reti-like Problems.......................357 14.6 Historical Remarks.................................................359 Future Challenges.......................................................361 References..............................................................363 Index...................................................................377 Chess Endgames |
|
|
| PREFACE |
|
This book is neither about linguistics nor geometry. It is about search problems. Linguistic Geometry (LG) is an approach to construction of mathematical models for knowledge representation and reasoning about large-scale multiagent systems. A number of such systems (formally defined here as Complex Systems), including air/space combat, robotic manufacturing, software re-engineering, Internet cyberwar, etc. can be modeled as abstract board games (ABG). These are multi-player games whose moves can be represented by means of moving abstract pieces over locations on an abstract board. The dimensions of the board (2D, nD, and even non-linear space), its shape and size, the mobility of pieces, the turn of moves (including concurrent moves) - all can be tailored to model a variety of multiagent systems. Thus abstract board games are understood here as a class of Complex Systems. The purpose of LG is to provide strategies to guide the participants of a game to reach their goals. Traditionally, finding such strategies required searches for suitable branches in giant game trees. Such searches are often beyond capabilities of modern and even conceivable future computers. LG dramatically reduces the size of the search trees, thus making the problems computationally tractable. LG provides a formalization and abstraction of search heuristics of advanced experts. Essentially, these heuristics replace search by construction of strategies. The formalized expert strategies yield efficient algorithms for problem settings whose dimensions may be significantly greater than the ones for which the experts developed their strategies. Moreover, these formal strategies allowed to solve problems from different problem domains far beyond the areas envisioned by the experts. It is really fascinating that for certain classes of problems these expert strategies yield provably optimal solutions. To formalize the heuristics, LG employs the theory of formal languages (i.e., formal linguistics), as well as certain geometric structures over the abstract board. Since both, the linguistics and the geometry, were involved, this approach was named Linguistic Geometry. This is the first book on the subject. It is not my intention to present a complete theory of LG, because such a theory is yet to be completed. However, the book includes foundations of such theory. LG already has a long and enlightening history. Chess, a Drosophila of Artificial Intelligence, contributed in a major way to the origin of LG. It continues to be an everlasting source of ideas and a driving force behind its development. Having started with computer experiments in 1972, continued with theoretical insights in the 80s, and formally established in 1991, LG has moved in many directions. Some of them are based on rigorous foundations, others - on sophisticated experiments. The purpose of this book is to introduce the reader to a multiplicity of approaches, ideas, and experiments. Every chapter is written as an essay on one topic in LG, theoretical or experimental, though all chapters are linked together and support each other. Chapter 1 includes introduction to the subject and a brief research background. Chapter 2 includes basic definitions and a survey of the LG formal tools, a hierarchy of formal languages. Chapters 3 through 7 cover a number of experiments with LG tools. They demonstrate how the LG algorithms solve problems of gradually increasing complexity. Besides interesting actual results, a detailed description of experiments is intended to develop an intuitive understanding of LG algorithms and their underlying structure. Armed with this intuition, a reader will be able to digest a formal description of LG tools in Chapters 8-12. Chapter 13 gives a new, much deeper account in the foundations of LG. By redeveloping the experiment from Chapter 3, it points a new direction in LG: solving search problems by construction of strategies (without any tree-based search). In Chapter 14 we discuss some issues of computational complexity. The book suggests that LG tools allow us to identify a wide subclass of tractable (polynomial) problems among those that are usually considered as intractable (exponential). The LG algorithms provide their solutions. This book can be used as a textbook for a graduate or senior undergraduate course on LG for one or two semesters or a supplement to a course on AI. Some of this material was taught in the courses Knowledge Representation for Intelligent Systems and Complex Intelligent Systems at the University of Colorado at Denver. Also, many topics included in the book were presented as tutorials and short courses on LG around the world. I hope that the reader will share my excitement with the subject and join the army of researchers and practitioners that develop the theory and applications of LG. The book is not going to be an untouchable sacred source of information on LG for decades to come. My intention is to move the frontier, elicit interest, ignite research and development, to bring this book out of date, and write a new book that will further revolutionize our understanding of the subject. Boris Stilman, Denver, Colorado, USA |
|
|
| ACKNOWLEDGMENTS |
|
It would have been impossible for me to write this book about Linguistic Geometry if it was not based on almost three decades of research. This research would have never advanced to the current level without major support of my adviser, colleagues and scientists from around the world, funding agencies, and computing centers. This book was inspired by the results of long and fruitful collaboration in the 70s and 80s with Professor Mikhail Botvinnik, my research adviser and project director. At the very beginning he shaped my thinking about complex search problems. One scientist said that this unimaginably difficult work could have started because Botvinnik, a chess player, did not anticipate the difficulties of programming, while Stilman, a computer scientist, did not anticipate difficulties of playing chess. Every time when the team of researchers experienced serious problems in the development of the project PIONEER, Dr. Botvinnik used to say: “If a human chess master can make it, a computer will make it as well”. He believed in the existence of a general algorithm, or a small collection of general algorithms, used intuitively by all the chess masters and grandmasters in playing chess. Essentially, discovery, simulation and generalization of these algorithms were the goals of the project PIONEER. An attempt to construct and investigate a mathematical model based on those algorithms is the goal of this book. Alexander Yudin, Alexander Reznitskiy, Mikhail Tsfasman, Mikhail Chudakov have worked with me in the 70s and 80s to develop project PIONEER. My friend and colleague, Vadim Mirniy, with whom we worked in the 80s provided major insights and pushed our research and software implementations to much higher level. Also, in the 70s an invaluable technical assistance in software development was provided by Dmitry Lozinskiy, Lidia Poltavets and Anatoliy Kostrukov. Four major scientists, the founders of computer science and engineering in the former Soviet Union, Academician Viktor Glushkov, Professors Bashir Rameev, Viacheslav Myasnikov and Nikolay Krinitskiy contributed to the establishment of the organizational framework, provided major funding and access to the state-of-the-art computers for project PIONEER. Project PIONEER and the first theoretical generalizations related to the origin of LG would have never succeeded without constant support of numerous Soviet scientists. I am grateful to all of them. Here, I would like to acknowledge those whose decisive support came at the most difficult times. They are Academician Nikolay Krasovsky, Academician-correspondent, Lenin Prize Winner Yakov Tsipkin, Academician-correspondents Yury Rudenko and Hermogen Pospelov, Professors Dmitry Pospelov, David Yudin, Vladimir Yakubovich, Georgiy Adelson-Velsky, Yuriy Shakarian, Gavriil Shalit, Lev Mamikoniants and Dr. Mikhail Donskoy. Scientific exchange with researchers from around the world allowed our team to overcome isolation of the former Soviet Union. A list of major participants of this exchange includes Professor Monty Newborn from McGill University, Canada, Professors Tony Marsland and Randy Goebel from the University of Alberta, Canada, Professor Jaap van den Herik from the University of Limburg, The Netherlands, Professor Ben Mittman from Northwestern University, USA, Dr. David Cahlander from CDC Corp., USA, Ken Thompson from Bell Labs, USA, Dr. Hans Meuer from the University of Mannheim, Germany, Dr. H.-J.Appelrath from the University of Dortmund, Germany, David Levy from London, UK. I have a special debt to Professor Newborn who invited me to do research at McGill University in 1990. I am certain that without this invitation I would not have been able to continue research in LG. In 1992, Professor Ervin Rodin from Washington University, St. Louis, MS, showed interest in further development and expansion of LG. As an editor-in-chief of the international journal Computers and Mathematics with Applications, he wrote: “... I would be very interested in publishing these types of works of yours [in LG - B.S.]” (Rodin, 1992). Some of the major results presented in this book were first published in this journal. Professor Rodin’s Center for Optimization and Semantic Control at Washington University contributed to the success of the First Symposium on LG and Semantic Control in 1995. In 1994, with respect to applying LG to combat simulation and control, he wrote: “I am familiar with Professor Stilman’s work on Linguistic Geometry and I believe that it may be a most worthwhile tool to attack the above-named subject [intelligent battlefield planning and control - B.S.]” (Rodin, 1994). In 1993, Dr. Raymond Lauzzana, an editor-in-chief of the international journal Languages of Design demonstrated interest in broadening the scope of the LG audience. He put a significant personal effort, guidance, and encouragement in my revising of the paper on LG for his journal to make it available for a multidisciplinary audience. He wrote: “... I would like to say that Dr. Stilman has an exciting and refreshing interdisciplinary attitude about his research. He has been able to expand his research in modeling two-player games into a general model for hierarchical systems. This greatly expanded the applicability of his work ... I personally appreciate the rigor with which he has approached the subject. I am sure that his work will have a substantial influence in the future” (Lauzzana, 1993). Jim Rash, a scientist from NASA Goddard Space Flight Center, Greenbelt, MD, provided support, impetus and encouragement for further development of LG. As a guest editor of the special issue of the international journal Telematics and Informatics (with the best papers of the 1994 Goddard Conference on Space Applications of AI), he referred to my paper "Heuristic Networks for Space Exploration" (1994c), “...as an example of a particularly enticing application of AI ... This paper presents Linguistic Geometry as an efficient method for searching large solution spaces with respect to classes of problems that are known to be especially difficult, and applies the method to the problem of autonomous robot navigation planning” (Rash, 1994). I am grateful to Professor Alex Meystel from Drexel University, for his constructive interest in LG and continuous support. As an editor-in-chief of Wile Series in Intelligent Systems he not only encouraged me to complete this book at the very beginning of this work but already urged me to write another book on LG, maybe with different emphasis. Professor Meystel wrote: “... I would expect that multiple new results of LG will be incorporated by Knowledge Engineering in AI. Any further advancement in this area is unthinkable without taking advantage of the conceptual systems like Linguistic Geometry” (Meystel, 1998). A skeleton of the book was implicitly influenced by Professor Norman Foo from the University of New South Wales, Sidney, Australia , who wrote: “There cannot be any panaceas for search techniques as it is provable that the worst case is exponentially hard or worse. So, for any given idea, there will be classes of problems that will defeat it. However, it is entirely possible that large subclasses of problems that have good descriptions are susceptible to efficient attack. This is where Boris’ ideas in linguistic geometry come into their own. He has essentially found an interesting and useful subclass for which his ideas and representation promise efficient solutions. This is a significant contribution to the area” (Foo, 1996). When the work on this book was almost completed, I learned about the following statements by Professor John McCarthy from Stanford University. In his comments about solving R.Reti chess endgame by computers he wrote: “Note that Reti’s idea can be implemented on a 100x100 board, and humans will still solve the problem, but present [conventional, i.e., brute force - B.S.] programs will not... Chess can serve as a Drosofila for AI if AI researchers try to make a program that (will) come up with the idea needed to solve the problem on a board of arbitrary size. Conversely, AI will not advance to human level if AI researchers remain satisfied with brute force as a substitute for intelligence... Would anyone seriously argue that it is impossible for a computer to solve the Reti problem by other than brute force?” (McCarthy, 1998). Of course, LG was developed independently and over a long period of time. However, it is fascinating that this research was driven by similar ideas. LG benefited greatly from the unique expertise of two scientists, my friends Dr. Vlad Yakhnis from Rockwell Science Center, CA and Dr. Alex Yakhnis from Pioneer Technologies, TX. They made significant contributions to the construction of winning strategies for two player games with perfect information. Their work influenced the definition of abstract board games employed by LG. I extend my special thanks to Dr. Vlad Yakhnis who contributed greatly to the re-development of the foundations of LG. I would like to express my sincere appreciation of Dr. Alex Yakhnis’ review of the draft of this book and his constructive comments. I thank my student David Knox for reading the draft of this book, for his invaluable comments, and for saying that this book is ... certainly readable. I use this opportunity to thank my friend Professor Tom Altman from the University of Colorado at Denver whose inspirational ideas and practical advice helped me significantly advance the theory and applications of LG. It is very important to have a friend you can rely on in the most difficult situations in research and beyond. I am grateful to my son Michael, currently a freshman at Stanford, who contributed to the development of LG for the agents with variable speed and designed an amazing cover for this book. Another person whom I would like to distinguish is Gary Folven, my publisher. His enthusiasm about this book and unimaginable patience helped me to successfully complete this work. In this brief survey it is impossible to acknowledge all the contributions. I would like to express my gratefulness to numerous researchers, practitioners, and students whose interest and efforts helped to clarify and advance various aspects of LG. While in the USSR, this research was supported by the grants from the State Committee for Science and Technology (GKNT) and from the Department of Energy and Power Production (MinEnergo). An access to the most advanced computers was provided by the Computing Center of the State Planning Committee (GVC Gosplana), the Computing Center for Information on Science and Technology (VNTIC), and the Computing Center for Health Maintenance of the Government of Moscow (VCKP "Zdravoohranenie"). For many years a friendly, supportive environment of the National Research Institute for Electrical Engineering (VNIIE) assisted me in the development of LG. While in Canada and in the USA, this research at various stages was supported by the National Sciences and Engineering Research Council (NSERC) of Canada and McGill University, by the U.S. Air Force Office of Scientific Research (AFOSR) via Summer Faculty Fellowship at the Air Force Phillips Laboratory, by the grant from the Department of Energy through Sandia National Laboratories, and by the University of Colorado at Denver Faculty Research Fellowship. Currently, this research is supported by a substantial grant from the Defense Advanced Research Projects Agency (DARPA). |
|
|
| 1 INTRODUCTION |
|
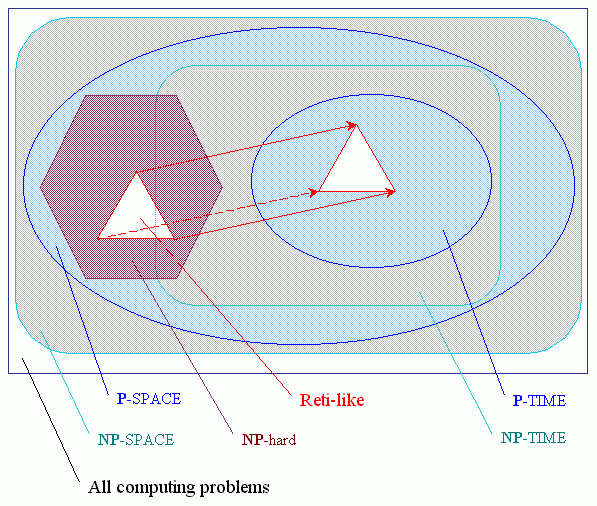
Linguistic Geometry includes the syntactic tools for knowledge representation and reasoning about multiagent systems by modeling them as abstract board games. The LG tools provide a basis for the evaluation of computational complexity and accuracy of solutions, and for generating computer programs for specific problem domains. LG allows us to discover the inner properties of human expert heuristics that are successful in a certain class of games. This approach provides us with an opportunity to transfer formal properties and constructions from one problem to another and to reuse tools in the new problem domain. In a sense, it is the application of the method of a chess expert to robot control or maintenance scheduling and vice versa. What do we know about the methods of a chess expert? Of course, a computer is the perfect tool for discovery and modeling of such methods. The history of computer chess began with a paper by Professor Claude Shannon (1950) in which he introduced the framework that guided further development. Employing mostly the brute force search, relying ultimately on computer speed, computer chess programs gradually increased their level of playing (Newborn, 1996). In the middle of the 90s, they reached the level of a grandmaster. After the May 1997 historical event, when the Deep Blue computer chess system defeated World Chess Champion Gary Kasparov, computer chess lost its exciting attractiveness. In June of 1997, Professor John McCarthy wrote: “In 1965 the Russian mathematician Alexander Kronrod said, «Chess is the Drosophila of Artificial Intelligence». However, computer chess has developed much as genetics might have if the geneticists had concentrated their efforts starting in 1910 on breeding racing Drosophila. We would have some science, but mainly we would have very fast fruit flies” (McCarthy, 1997). All the major advances in computer chess, including the Deep Blue triumph, were related to the brute force approach. What can we learn from these advances for different problems, particularly, for the problems of much higher dimension? Not much. Even in the future, we will not be able to solve these problems employing brute force. The grandmaster’s approach (of almost no search) has not been discovered yet. After the 1997 event, it is more important than ever before, that chess stays as a scientific Drosophila of AI and not just a racer (McCarthy, 1990, 1997). Not all the research in computer chess went in the direction of the brute force. In the 70s and 80s project PIONEER led by the Former World Chess Champion, Professor Mikhail Botvinnik was developed in Moscow, Russia. In his book (1984) Botvinnik writes that the brute force method is “hardly capable of further progress. It is the computer’s turn to adopt a more fruitful method - perhaps PIONEER. And if PIONEER is unsuccessful, we must believe that other method will be found. The problem must and will be solved”. LG is the direct successor of the project PIONEER. The Drosophila of AI “flies through this book fertilizing various experiments and generating new ideas”. Among other examples in this book we consider a series of combat simulation problems. These are Reti-like problems, i.e., the generalizations of the R.Reti endgame (c.f. Botvinnik, 1984). Here they are called 2D/4A, 3D/4A, partially and totally concurrent combat simulations. These problems are simple enough to be used as demonstrations of the LG approach. On the other hand, they are not trivial and require significant search to be solved employing conventional approaches. It is the general understanding that they are P-SPACE-complete or at least NP-hard and no known polynomial-time algorithms exist to solve them (Garey and Johnson, 1991). LG tools allow us to solve subclasses of these and many other problems employing algorithms of polynomial complexity. It can be suggested that the Reti-like problems are representative of a wider class of problems of low (polynomial) computational complexity. This would be a new subclass in the class of P-TIME problems. It is likely that many important real world problems considered below are members of this subclass. |
|
|
|
Exist the classes of problems polynomial-time:
P-TIME ⊆ NP-TIME ,
NP-complete=NP-hard ∩ NP-TIME
and polynomial-size:
NP-hard ⊆
P-SPACE ⊆
NP-SPACE ,
here P - deterministic polynomial,
NP - nondeterministic polynomial.
The simplified classification of problems on computing complexity.
|
|
|
| 1.1 Problems |
|
Advanced technologies are required for simulation of various concurrent multiagent systems such as land combat operations, aircraft combat missions, tracking and possible interception of missiles and satellites, surveillance operations, etc. Unmanned aircraft or tanks may participate in reconnaissance missions or in the full scale combat operation. Similar teams of intelligent vehicles may be dispatched by the adversary. Control of those actions requires permanent adaptation to the intermediate results and dynamic re-computation in real time. One example is the problem of real time control of the air combat in which a number of planes (manned or unmanned) equipped with countermeasures evade a number of pursuers equipped with missiles. Another example is the problem of optimal control of unmanned aerial vehicles (UAVs) that are in the reconnaissance flight to locate mobile missile launchers. The actual launch points are usually detected by satellite-based sensors. The UAVs use detected launch points to initiate their search, locate and possibly destroy them. In the real world scenario, the UAVs control should be considered together with the air combat when UAVs evade a pursuing enemy aircraft and, on their turn, pursue adversarial mobile launchers. Similar problems of the development and real time replanning of the combat scenarios are essential for the navy and army battlefields. Conventional models of combats can achieve computational and, sometimes, analytical solutions for the simple cases. Real world cases employing those approaches are, however, computationally intractable. Space combat simulation problems are, in general, similar to the other combat simulations. However, the astrodynamics of the spacecraft makes these problems significantly more complex. Another factor is the vehicle’s autonomy. While the autonomy of the land, navy, and aerial vehicles is highly desirable, it is essential for the spacecraft, especially, if they are far away from Earth. Simulation and control of the two-three spacecraft combat requires enormous amounts of computations. Problems with greater number of vehicles are computationally intractable (Shinar, 1990; Garcia-Ortiz, et al., 1993). Another class of problems is related to intelligent manufacturing in industrial environment. Groups of robots move around the plant, collect assembly parts, deliver them to the assembly line, and assemble the product. Because of the localized control, robots collaborate only within their groups. Various groups compete with each other for common resources including parts, movement paths, assembly queue, etc. Planning of these activities requires an enormous amount of computation employing conventional approaches. Problems of software re-engineering require conversion of unstructured programs into the object-oriented software where, sometimes, the end product of such conversion must be provably correct. This conversion is intended to transform original unstructured, the so-called legacy software, into a product which must be maintainable. This class of problems can be reduced to the problems of graph transformation where the original graph represents the software to be converted. Typically, this is done employing graph-rewriting systems. While small-scale software is convertible, an attempt to scale up to the real world software poses a tremendous computational challenge. Problems of network security, integrity, and problems of the Internet cyberwar have recently attracted significant attention. The question is how to protect the national computer network from an attack of billions of computer viruses and worms? Which nodes and even branches should be cut off (sacrificed), which should be revitalized by activation of duplicates, what countermeasures should be engaged? A conventional response to this threat is by local protection. It appears that the amount of computation required to generate a strategy for global protection makes this problem intractable. Scheduling problems with resource allocation are ubiquitous. They include scheduling jobs in industrial environment by selecting them from the queue of demands and by delivering resources to job location. Usually, not all the demanded jobs can be scheduled because of the shortage of resources while the number of demands can exceed thousands. How to schedule the most important jobs in order to obtain the best schedule? One of such problems is scheduling of maintenance of power units in a number of power plants. Each maintenance requires the unit to be shut down and, consequently, to compensate the loss of power by the power reserve from other power plants. These problems are known to be, in general, computationally intractable (Garey and Johnson, 1991). Programming the game of chess is not necessarily practical but certainly a challenging problem. It is most attractive because, in contrast with many others, true human experts like grandmasters and world champions do exist. Some of them are capable of the analysis by introspection and by comparison with the computer game models. This gives us a chance of successful discovery and formalization of their approach, and the possible transfer to different problem domains. |
|
|
| 1.2 Current Approaches |
|
Problems of long and short-range mission planning, especially for autonomous navigation, aerospace robot control, such as UAV, aerospace combat operations control, global and local reconnaissance, etc., are usually described mathematically in the form of pursuit-evasion differential games. The classic approach based on the conventional theory of differential games (Isaacs, 1965) is insufficient, especially in case of dynamic, multiagent models (Lirov, Rodin et al., 1988; Garcia-Ortiz, et al., 1993). It is well known that there exists a small number of differential games for which exact analytical solutions are available. There are a few more for which numerical solutions can be computed in a reasonable amount of time, under rather restrictive conditions. However, each of these games must be one-to-one, which is very far from the real world combat scenarios. They are also of the "zero-sum type" which does not allow a new agent to join the game or some of the agents of both sides to be disengaged. Other difficulties arise from the requirements of the 3D modeling, limitation of the lifetime of the agents, or simultaneous participation of the heterogeneous agents such as on-surface, undersea, and aerospace vehicles. Following (Rodin et al., 1987, 1988; Rodin, 1988; Shinar, 1990), discrete-event modeling of complex control systems can be implemented. These techniques can be based on generating geometrically meaningful states. By discretization time, a finite game tree can be obtained. The nodes of the tree represent the states of the game, where the players can select their controls for a given time increment. It is also possible to distinguish the respective moves of the adversarial sides (including simultaneous actions). Thus, the branches of the tree are the moves in the game space, and these problems can be viewed as planning problems in AI. The main difficulty is the combinatorial explosion of the search tree. According to (Lirov, Rodin et al., 1988) “... In the case of the two-plane game, the problem of model choice is not too great, so an exhaustive search for the best model can be performed in a reasonable amount of time. However, the search problem becomes a primary concern when ever all planes are participating in the game or, in a more complicated example, some other objects are introduced, such as obstacles at some future times”. How do we handle this combinatorial explosion? Can we reduce an average number of alternatives considered in each position (state), ultimately, to one alternative? This would be an ideal algorithm, one that is able to find a solution without any tree-based search. The branching factor B is a parameter representing the average breadth of the search tree. It shows how many moves (on the average) should be included in this tree at each node. For example, in the game of chess applying the brute force search algorithm, we have to include all the legal moves (permitted in every position according to chess rules). This means that we have to generate a search tree of the size T which can be calculated following (1.2.1). In this equation, B is the average number of moves in each position, L is the depth of the search (assuming all the branches are terminated at the depth L), and T is the total number of positions generated. The computation of B is based on the consideration of a hypothetical search tree with the depth of all branches equal to L, total number of moves equal to T, and a constant number of successors of each node. By definition (Nilsson, 1980; Rich and Knight, 1991), this constant number is equal to the branching factor B and is determined as a solution of the equation (1.2.1) for given L and T relative to B. Greater values of B correspond to a non-selective search; obviously they indicate an exponential growth of the search with a big base. Algorithms that reduce B, especially those algorithms which make B close to 1, should be considered as extremely goal-driven with minimal branching to different directions. Employing (1.2.1) for the total number of moves T actually generated during the search and the value L of the required depth of the search, we can calculate the branching factor B for an arbitrary search algorithm. It can be found as an approximate solution of the equation (1.2.2) with respect to B. This is a non-linear equation and, usually, it is being solved by various methods including the trial and error approach. |
| B + B2 + ... + B L = T | (1.2.1) |
| or | |
|
B L+1 - 1 ————— = T . B - 1 |
(1.2.2) |
|
Various search algorithms, such as dynamic programming and branch-and-bound algorithms, were constructed in order to reduce the branching factor. For the two-player opposing games, such as the game of chess, the most popular algorithms are various search algorithms with formal alpha-beta pruning (Nilsson, 1980; Rich and Knight, 1991). They are implemented in the most powerful computer chess programs, e.g., in all the programs which are current and former World Computer Chess Champions. It was proved that in the best case the alpha-beta search algorithm can reduce the number of terminal nodes to be visited as follows (Slagle and Dixon, 1969; Knuth and Moore, 1975):
This number of nodes has to be searched in any case, even with perfect move-ordering procedure. All the various modifications of the alpha-beta search can do no better than this best case (Kaindl, 1990). However, the tree still grows exponentially, albeit with a reduced exponent. The perfect ordering can theoretically double the search depth (during the same time frame) employing the reduced branching factor to approximately √B. Through this book we use √B, as a value of the reduced branching factor in our comparison of the alpha-beta best case results with the results obtained employing the LG tools. Assume that an arbitrary chess position, on average, contains about 40 legal moves, then alpha-beta pruning can reduce this number to approximately 6 (≈√40). Still, we have an exponential growth with a very high base B=6 (high branching factor). As a result, chess problems that require a deep search, for example, to the depth of L=20 or more moves, need enormous amounts of processing time to be solved. Even the Deep Blue hardware-software system cannot make this leap (Hsu, et al, 1990; Newborn, 1996, 1997). This massively parallel system of special-purpose chess chips with a processing speed of two hundred million positions per second fall short in an attempt to overcome the exponential growth that comes with a high branching factor. In real world problems the number of alternatives is far greater than 40, while required depth sometimes exceeds hundreds of moves. Even future super-computers will not be able to handle this amount of computations employing conventional search procedures. One of the basic approaches is to decrease the dimension of the complex system following the approach of a human expert in the field, by breaking the system into smaller subsystems. This process of decomposition can be applied recursively until we end up with a collection of basic subproblems that can be treated (in a sense) independently. This can be viewed as planning in presence of subgoals, macro-operators, and abstraction (Korf, 1987; Tate, Hendler and Drummond, 1990). At each level of decomposition we can apply an abstraction by initially ignoring the low-level details and concentrating on the essential features of the problem, addressing the details later. To a certain degree, human experts usually establish subgoals (and reach them) because they know what sequence of operators (macro-operator) to apply to reach the next subgoal. The idea of abstraction in human problem-solving was pointed out in (Polya, 1945), later, it was used in the planning version of GPS (Newell and Simon, 1972). Since then, similar ideas have been developed in many systems within formal theories of linear and nonlinear planning (e.g., Sacerdoti, 1974, 1975; Stefik, 1981; Chapman, 1987; Knoblock, 1990; Georgeff, 1990; McAllester and Rosenblitt, 1991) or within different approaches (Mesarovich and Takahara, 1989; Albus, 1991). Real world complex systems usually involve dynamic processes beyond the control of a single agent. The problem solver should reason about actions that the agent has no control over and that may or may not occur concurrently with what the agent is doing. A number of theories of planning for multiagent domains have been developed in (Allen, 1984; Georgeff, 1983, 1990; McDermott, 1985; Pelavin and Allen, 1986). In particular, an event type can be considered as a set of state sequences, representing all possible occurrences of the event in all possible situations, which might include concurrent actions of multiple agents. One of the possible approaches is to approximate concurrent activity by using an interleaving approximation (Georgeff, 1983; Pednault, 1987). We use the same approximation in our first examples (Chapters 3, 4, 5, and 6). Of course, it is not possible to model simultaneous events within this approach, and we introduced true concurrency to handle that (Stilman, 1995d, 1997a; Skhisov and Stilman, 1997, 1998a, 1998b, and Chapter 6). Besides a number of specific problems, including inherent the ambiguity of decision making for an agent due to immediate simultaneous actions of other agents, the major problem of one-agent planning remains and even amplifies dramatically for multiple agents. This is the problem of combinatorial explosion of the search space. Introducing concurrency by allowing moves with all the simultaneous combinations of actions results in a tremendous growth of the branching factor, and, consequently, in the growth of the search space (Chapters 6, 13, and 14). None of the conventional approaches to the problems considered in Section 1.1 allows us to scale up to the real world concurrent systems with respect to the number of agents, dynamic change of their capabilities, size, shape, and dimension of the operational district, concurrent actions, real time requirements, etc. One of the main difficulties is the enormous complexity of computations due to the exponential growth of the number of variants of the system’s operation to be analyzed. Fortunately, there are many such problems where the human expert skills in reasoning about complex multiagent systems are incomparably higher than the level of modern computing systems with respect to complexity reduction. Though there is no grandmaster in combat simulation or robot control, in the game of chess, the human grandmasters have achieved amazing results in search reduction. Our goal is to study human expert reasoning in the areas where the results are successful, in order to discover the keys to their success, and then apply and adopt these keys to the new, as yet, unsolved problems. As we discussed above, one of the main search heuristics of a human expert is related to the decomposition of the system into subsystems. This decomposition has been implemented for many classes of problems with varying degrees of success. Implementations based on the formal theories of linear and nonlinear planning encounter efficiency problems. An efficient planner requires an intensive use of heuristic knowledge. On the other hand, a pure heuristic implementation can hardly be reproduced for other problem domains. Each new problem should be carefully studied and previous experience usually cannot be applied. Is there a general constructive approach to such implementations? What are the formal properties of expert’s heuristics which drove us to a successful hierarchy of subsystems for a given problem? How can we apply the same ideas for a different problem domain? We need formal language tools for an adequate representation of expert skills. An application of such tools to the area of successful results achieved by the human expert should yield a formal, domain-independent knowledge ready to be transferred to different areas. Neither natural nor programming languages satisfy our goal. The first are informal and ambiguous, while the second are usually detailed, lower-level tools. We have to learn how we can formally represent, generate, and investigate a mathematical model based on the abstract images extracted from the expert’s vision of the problem. |
|
|
| 1.3 LG Approach at a Glance |
|
Linguistic Geometry (LG) includes the syntactic tools for knowledge representation and reasoning about multiagent complex systems. LG has been developed as a generic approach for a certain class of complex systems. This approach gives us powerful tools for reducing the search in different complex problems by decomposing the complex system into a hierarchy of dynamic interacting subsystems. LG allows us to study this hierarchy formally, investigating its general and particular properties. These tools provide a framework for the evaluation of the complexity and quality of solutions, and for generating computer programs for specific applications. The purpose of LG is to provide solutions to a variety of problems with huge state spaces, where it is desirable to find optimal or "the best you can do" behavior of entities generating purposeful transitions from state to state. Such problems include cooperation/competition of teams of intelligent (or human guided) robots (e.g., for ground or seagoing vehicles, aircraft, or spacecraft); safety-critical control systems for the remote fully automatic objects like planetary exploration vehicles; VLSI design; planning, scheduling, and resources distribution; chess, etc. Traditionally, finding optimal or near-optimal behavior of entities for the above systems required searches for suitable branches in giant game trees. Such searches are often beyond capabilities of modern and conceivable future computers. The LG approach dramatically reduces the size of the search trees, thus making the problems computationally tractable. Although discrete by its nature, the LG approach could also be applied to the control of continuous processes described by ordinary or partial differential equations, albeit after a discretization of the equations. One of the unique features of the LG approach is the formalization and utilization of search heuristics developed by highly-skilled human experts (including chess grandmasters). These experts have developed sophisticated and successful strategies resulting in tremendous search reduction in their domains. However, before the present work, the methods behind the experts’ heuristics and intuition were not understood by the AI scientists or even by the experts themselves. Based on the theory of formal languages, geometrical insight, and the powerful apparatus of modern formal logic, we formalized and generalized these heuristics, thus enabling them to be applied to a vast class of problems. Prior to this work, most of these problems were not considered by experts to be in the areas of applicability of their heuristics. The results of comparison of the LG approach with other methods are roughly sketched in Fig.1.1. Three different search trees are shown. The top triangle reflects the search tree to be generated employing the brute force Search. Due to the high branching factor this tree is wide. However, because time is limited, all the branches must be terminated (for example, at the same depth). The tree generated by applying alpha-beta search algorithm is deeper and narrower. This is the result of cutoffs that allow us to reduce the branching factor and search deeper branches within the same processing time. It is proved that the optimal branch will not be pruned; it will be the same as in case of the brute force search with the same depth (Knuth and Moore, 1975). However, even in this case, the exponential growth with significant branching factor does not allow us to solve most real-world problems. The third, a very narrow and deep tree reflects the LG-search the branching factor is either close to one or exactly one. It has also been proved that for certain classes of problems the LG algorithm is a winning (draw) strategy (Chapter 13). |
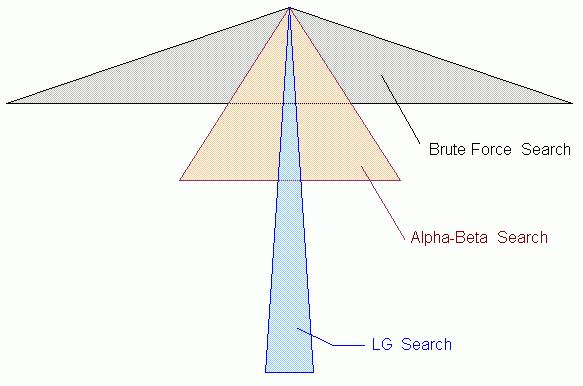
Figure 1.1 Comparison of searches for the same processing time. |
|
LG approach is applicable to the concurrent multiagent systems. Who are those multiple agents? Let us introduce two types of agents. Agents of the top level, the super-agents, are fully capable of acting by means a number of mobile entities, the local agents. The environment may have a profound impact on the movements of agents. Some of the locations may be reachable in a certain number of steps, others may not be reachable at all. Consider systems with two super-agents that oppose each other. They are called the opposing sides. Usually, they pursue opposing goals. Each of them controls a team of local agents whose freedom of operation is highly restricted. Ultimately, in the examples considered in this book, the local agents do not have freedom at all and are fully controlled by a super-agent. However, the LG tools are applicable to models where the local agents are less constrained and operate autonomously with some distributed intelligence. Each super-agent develops a model of the opposing super-agent and operates assuming that the adversary will do its best within this model. The model is used for planning the agent’s actions and choosing the optimal one. The model establishes local goals for local agents. These local goals are coordinated with the global goal of the corresponding super-agent. Motions directed to the local goals are intended for a super-agent to achieve the global one. The model is dynamic: after every action, which may include concurrent movements of agents of both sides, it is updated taking into account the new situation. The dynamic model can be viewed as a hierarchy of subsystems. We introduce local goals by decomposing the system of local agents into subsystems striving to attain these goals. For example, each second-level subsystem includes local agents of both opposing sides: the goal of one side is to attack and destroy another side’s local agent (a target), while the opposing side tries to protect it. In the robot control, for example, it means the selection of a pair of robots of opposing sides: one - as an attacking element, and the other - as a local target, generation of the local paths for approaching the target, as well as the paths of other robots supporting the attack or protecting the target. In LG the hierarchy of subsystems is represented as a hierarchy of formal languages. To introduce formal languages following (Hopcroft and Ullman, 1979), we have to use symbols. A symbol is an abstract entity that we shall not define formally. Examples of symbols include
a,
t,
a(xi),
t(p2,
t2,
τ2),
π(i5)
etc.
A string (or word ) is a finite sequence of concatenated symbols. For example,
a(x1) a(x2) ... a(xn) is a string, if
a(x1), a(x2), ... , a(xn) - are symbols. An alphabet is a finite set of symbols.
A (formal) language is a set of strings of symbols from some alphabet.
The empty set,
Ø
, and the set {e} consisting of the empty string e - are languages. Consider a language
W and a string
w of this language. Alphabet of the string
w,
V(w), is a set of symbols whose members occur at least once in the string w. For example, the set
V={ a(x1), a(x2), ... , a(xn) }
is the alphabet of the string a(x1) a(x2) ... a(xn). A chart of the Hierarchy of Formal Languages is shown in Fig.1.2 as a building set of three types of triangles. Every state of the state space (the set of all positions, i.e., all possible configurations of agents) is represented by the 2-hierarchy, two embedded triangles (the Language of Trajectories and the Language of Webs). Several triangles that represent states together with their 2-hierarchies and additional attributes are embedded in one large triangle, a string of the Language of Translations. This top-level language includes a solution of the problem. A detailed presentation of the LG Hierarchy of Languages begins in Chapter 2 and continues in Chapters 8-12. A more elaborate illustration of the chart is shown in Fig.1.4. Below, we give a preliminary, brief introduction to this Hierarchy. |
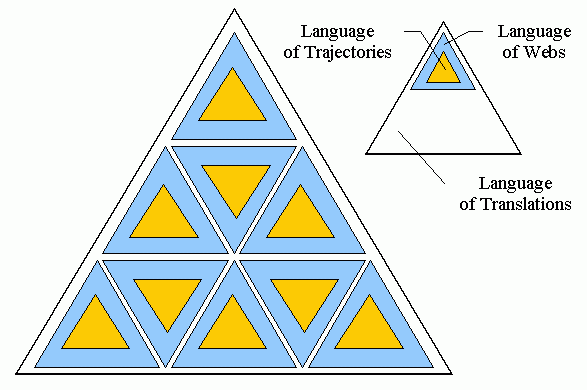
Figure 1.2 Hierarchy of subsystems as Hierarchy of Formal Languages. |
|
The first-level subsystems in LG are represented by the Language of Trajectories that is the set of "trajectories", the following strings of symbols:
where xi are called parameters. Values of parameters incorporate the semantics of problem domain. Strings of this type represent paths (trajectories) of local agents. For example, for a robotic model, xi are the coordinates of the robot’s planning path. The second-level subsystems in LG are represented by the Language of Webs, which is the set of "webs" or "networks", the following strings of symbols:
where pi , ti , τi are called parameters; pi is a local agent of the system (a robot or a software agent), ti is an entire trajectory of the agent pi, a τi is a list of domain-specific parameters. These networks represent a framework for dynamic tactical planning. The agents move along the paths (trajectories) attempting to achieve local goals, while advancing the achievement of the global goal of the super-agent, such as victory in a combat or the best schedule of a power-producing system. There may be many levels of network languages representing a hierarchy of subsystems. The entire system operates by changing from one state to another. That is, the movement of a local agent from one point to another causes an adjustment of the hierarchy of languages. This adjustment is represented as a mapping, a translation, from one hierarchy to another, or, more precisely, to a new state of the same hierarchy. The search for a strategy generates a number of paths (sequences of moves) through the state space which can be considered as series of translations of the hierarchy of languages. In the top-level formal language in LG, the Language of Translations, every "search" is represented by a string of symbols:
where ik are called parameters. Each symbol π(ik), represents a move of a local agent along the network. Searches in the Language of Translations represent the actual searches for an optimal (suboptimal) operation, such as the winning strategy for a combat, the best maintenance schedule, etc. Generation in this language is controlled by interaction of networks. This generation results in a dramatically reduced search which yields a solution of a problem. |
|
|
| 1.4 LG Approach: Deeper Account |
|
A class of problems to be studied are the problems of optimal operation of an LG system, a Complex System. This system is defined (DEF 2.1-2.4) as a twin set of elements (local agents) and points (locations), where elements are units moving from one point to another. It is a very general representation, e.g., in robot control problems elements are autonomous robots moving along a path (constructed of the points) through a complex hazardous 2D or 3D environment. The elements are divided into two or more opposing sides (super-agents), although, in this book, we consider only two-side systems. Each side can attack and destroy opposing elements and protect friendly elements. A destroyed element must be withdrawn from the system but it can reappear in another situation. A withdrawal happens if an attacking element comes to the point where an element of the opposing side stands. Each side aims to reach a set of specific configurations of elements. For example, this configuration may reflect a set of specific locations of friendly elements or a set of locations of elements of both sides with the maximum gain, the total algebraic value of the friendly and opposing elements destroyed and withdrawn from the system. The LG system operates by moving from one system’s state to another. That is, a move of a player, being a relocation of an element of that side (player) from one point to another, causes a transition from a current system’s state to another state. For example the set of desired configurations of elements can be considered as a set of target states. Every state can be described by the list of elements (present at the state) and their locations. LG associates a hierarchy of structures with each state. A state has a structure of trajectories that are possible paths of movement of the elements which are present at the state. Each state, also, has the structure of Zones that represent all areas of local combat at the state. The structure of Zones is more complex than the structure of trajectories. The structure of Zones is based on the structure of trajectories. Thus, LG considers the structure of Zones being higher in the hierarchy than the structure of trajectories. The hierarchy of structures was originated from the hierarchy of subsystems introduced by the highly-skilled human experts. This introduction is as follows. A one-goal, one-level LG system (for each side) should be replaced by a multi-goal, multi-level system by introducing intermediate goals and decomposing the system down into subsystems striving to attain these goals. The goals for the subsystems are specific but coordinated within the main mutual goal. For example, each second-level subsystem, called a Zone, includes elements of the two opposing sides. The goal of one side is to attack and destroy the target, while the other side tries to protect it. In the robot control problems, this means the selection of a pair of robots of opposing sides: one - as an attacking element, and the other - as a local target, generation of a path for approaching the target, as well as the paths of other robots supporting the attack or protecting the target. A hierarchy of structures is represented in LG as a Hierarchy of Formal Languages where each string of the lower level language corresponds to a symbol of the higher-level one (Section 1.3). Following the LG approach, every first-level subsystem is represented as the following word, a string of symbols:
where each symbol a(xi) is taken from the alphabet of symbols { a(xi) }. Symbol a does not have special meaning except to link parameters xi in a string and indicate that this string is a trajectory. Values of parameters xi are defined by the semantics of the problem domain. Strings (1.4.1) form the Language of Trajectories (DEF 2.8). For example, for the robot control problem, xi - are the coordinates of the basic points of the robot’s planning path. For the maintenance scheduling problem, an analogous string represents a maintenance schedule variant for a specific power unit, where x1, x2, ... , xn correspond to the particular days of the scheduling period. Various types of trajectories are defined in Section 2.4. A second-level subsystem is represented also as a string with parameters, a web:
where symbol t like an a in (1.4.1) does not have special meaning except to link parameters in a string and indicate that this string is a web. Values of parameters (pi, ti, τi) are defined by the semantics of the problem domain and the lower level subsystems. Symbols pi represent elements of our system (robots, power units, etc.); ti represent trajectories (lowerlevel subsystems) of elements pi, i.e., strings
included in this subsystem, τi represent time allotted for movement along trajectory ti. Using strings (1.4.1), we can represent paths of system’s elements, and with the strings (1.4.2), networks of certain paths unified by the mutual goal. For example, in the robot control model such a network of planning paths represents a draft short-range plan for approaching a local goal in a hazardous environment, i.e., getting over the mobile and immobile obstacles. In the scheduling problem, it corresponds to the maintenance schedule of a certain power unit including the schedule for the provision of resources required. A set of strings (1.4.2) is called the Language of Webs (DEF 2.18). Various types of webs, the so-called Zones, are defined in Section 2.6. A transition to another state of the LG system causes an adjustment of the hierarchy of structures. This adjustment can be represented as a mapping (translation) to the hierarchy of structures of the other state. Actually, we can regard the change of the hierarchy of a state as that the hierarchy itself changes states. This means that at a state of the LG system the structures of associated Trajectories and Zones constitute a state of the hierarchy of structures. A directed state transition graph of a system induces a state transition graph of the hierarchy of structures. LG also introduces a higher level of the hierarchy of structures which is common to all states. Such a structure represents a game subtree and the corresponding states of the system that LG strategy for a player constructs in order to compute a move. This structure is called an LG-search tree (or LG-tree). The LG-search tree includes all the play variants that LG algorithm generates on the basis of a game state at which the player should make a move. The LG tree includes a very small subset of such variants as opposed to the full game tree. Let us restrict the term LG-search tree to coincide with a subtree representing LG variants used to compute a move for a player at a state of the LG system. The LG-search tree includes sequences of moves representing (or inducing) transitions between states of the LG system. Therefore, we can introduce another tree of corresponding sequences of mappings, translations of the hierarchy of languages (that represent these states). There exists a one-to-one correspondence between these trees. Thus, we will write about the same tree naming it either a tree of moves, or a tree of translations. This tree is represented as a string that enumerates the edges (the moves) of the tree in the order of, for example, depth first search tree traversal: π(i1) π(i2) ... π(in) in (1.4.3). The tree itself, then, can be written down as the pair of the string mentioned above, and the tuple of functions that produce the children of any tree node. Tuple functions includes a triple of functions that produce the left-most child, the left-most sibling, and the parent of any tree node. This tuple determines the signature needed to describe the algebraic structure of the tree by means of the children producing functions (DEF 2.26). Consider the following strings:
where every symbol π(ik) represents the following three items: - an edge (arc) of the LG-search tree, - a move, and - a corresponding translation. |
|
String (1.4.3) is a member of the top-level formal language, the Language of Translations (Section 2.8 and Chapter 12). Symbol π does not have special meaning except to link parameters in a string and indicate that this string is a tree of translations. Parameters ik are used to identify edges (arcs) of a tree. The list of functions called functions reflects links between the arcs: they are intended to support a tree data structure represented here linearly as a string of symbols. A construction of the LG tree (1.4.3) is controlled by generation and interaction of the webs (1.4.2) and trajectories (1.4.1). If LG algorithm is used by both players, a variant (or variants) that reflect application of LG strategy for both players is given by a certain branch of the LG-search tree. However, it need not be a (contiguous) substring of the string (1.4.3) of the Language of Translations. For example, consider a 4-node tree π(1) π(2) π(3) (Fig.1.3). Edge π(1) leads from the root R to the single child X, edge π(2) leads to the left child of X, and edge π(3) leads to the right child of X. The depth first search enumeration is π(1) π(2) π(3). The substring π(1) π(2) represents a left branch of the tree. There is another branch consisting of the sequence of edges π(1) and π(3), i.e., π(1) π(3). However, π(1) π(3) is not a contiguous substring of π(1) π(2) π(3). |
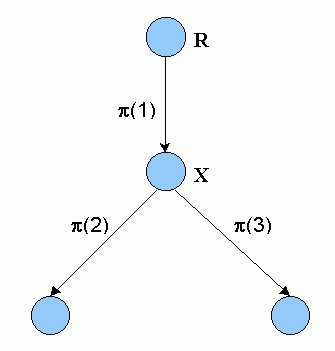
Figure 1.3 A 4-node tree π(1) π(2) π(3). |
|
If the LG algorithm is used by only one player, a play arising as an application of LG strategy for that player need not be a branch of the LG tree mentioned above. The reason is that the opponent may use moves that do not belong to the variants occurring in the LG tree. Because of the LG’s sophisticated algorithm selecting the variants, the opponents moves not belonging to the variants will be usually weaker moves. Often, LG strategy will recognize the weakness in the opponent’s response when constructing the LG tree for the subsequent moves. |
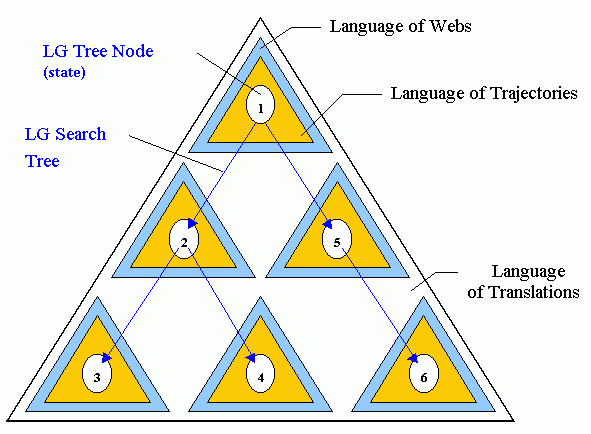
Figure 1.4 Hierarchy of Formal Languages in LG. |
|
A chart of the Hierarchy of Formal Languages is shown in Fig.1.4. This is a refinement of the chart shown in Fig.1.2. The Language of Translations is a language of trees (searches). A string of this language can be illustrated by a tree. One of such trees with 5 arcs and nodes 1-6 is shown in Fig.1.4. A node of this tree corresponds to a state of a complex system (1-6). Decomposition of the system into subsystems is represented in LG by the Hierarchy of Formal Languages. At every state the decomposition is represented by the hierarchy of two languages, the 2-hierarchy of the Languages of Webs and Trajectories. A string of the Language of Trajectories corresponds to a symbol of the Language of Webs. The 2-hierarchy is illustrated by the two embedded triangles attached to every node of the LG tree. A relationship between this hierarchy and the top-level Language of Translations (shown as one large triangle) is different from the relationship between the languages within the 2-hierarchy. A string of the Language of Translations, a search, represents an LG-search tree with nodes, that are linked to the states with attached 2-hierarchies. Therefore, the 2-hierarchies correspond to every symbol of a string of the Language of Translations. This is illustrated in Fig.1.4. An LG-search can be reflected as the generation of a string (LG tree) of the Language of Translations. The advantages of representing a decomposition of an LG system as a Hierarchy of Formal Languages become more apparent when we consider the formal mechanism for generating this Hierarchy. In pattern recognition problems, a formal linguistic approach was proposed for representation of hierarchical structured information contained by each pattern, i.e., for describing patterns by means of simpler subpatterns. This approach brings to light an analogy between the hierarchical structure of patterns and the syntax of languages. The rules controlling the merging of subpatterns into patterns are usually given by the pattern description grammars, with the power of such description being explained by the recursive nature of the grammars. Using similar approach for generating trajectories and trajectory networks, we make use of the branch of the theory of formal grammars developed in (Knuth, 1968; Rozenkrantz, 1969; Volchenkov, 1979; Stilman, 1985). A detailed account into the controlled grammars and their applications to LG is given in Chapters 8-12, 14. Recent investigation of the accuracy of the solutions generated by the LG algorithm resulted in a deeper understanding of the power of this approach. It appears that LG tools are able to implement a constructive decomposition of the state space (Chapter 13). These tools allow us to formally describe essential subsets of states and formulate intend-to-win strategies, the classes of paths in the state space leading from the Start State to the desired subset of states. Some of these strategies can be eliminated as non-implementable. The next step is an attempt of formal implementation of the non-eliminated strategies by each of the opposing sides. This is provably the best each side can do. Application of the intend-to-win strategy by each side results in the generation of a tree - the optimal solution of the search problem. Similar ideas work for various classes of games. Optimality is proved for the classes of multiagent serial and concurrent war games with d-dimensional operational district, a subset of Zd. This investigation led to the new direction in LG: solving search problems by construction of strategies without any tree-based search (Chapter 13). |
|
|
| 1.5 LG Strategies and Game Theory |
|
Consider the relationship between the LG strategies (for a super-agent of the LG system of two interacting super-agents) and the strategies of the game theory. Game theory emerged in the 1930s, e.g., (Von Neumann and Morgenstern, 1944), (Owen, 1982), and has a rich literature. A survey is given in (Luce and Raiffa, 1957). A significant branch of game theory is devoted to modeling economic behavior. In this branch, the goals of the players are stated by means of payoff function and by a requirement to maximize a player payoff. While LG employs an evaluation function that is a form of a payoff, the spirit of LG is closer to another branch of game theory that was initiated by Gale and Stewart (1953), and is called two player games with perfect information. The goals of the players in two player games are stated by means of desirable sets of plays, called winning sets. A winning strategy for a player is a pattern of behavior permitting the player to attain the winning set no matter what the opponent would do. The methods of constructions differ from those of games modeling economics in employing the methods of logic, algebra, and topology, rather than of mathematical or functional analysis, and/or variational calculus. Methods similar to variational calculus are also used in another branch of game theory called differential games, (Isaacs, 1965) and Section 1.2. Gale-Stewart games were extended to games over graphs due to work of A.Yakhnis and V.Yakhnis (1993) and Zeitman (1994). The earliest reference to the games over graphs are the classical papers on game theory such as (Kuhn, 1953) and (Berge, 1957). The games over graphs (1993-1994) were further extended to allow concurrent moves of more than two players (Yakhnis V. and Stilman B., 1995b). The latter games are closest to the abstract board games employed by the LG systems. The objectives of the graph games and those of LG are not identical since within the LG approach the class of useful strategies is wider than that of winning strategies. Intuitively, the LG-specific strategies could be understood as "the-best-you-can-do" strategies, rather than winning strategies. Indeed, often the LG games do not have a "deterministic" winning strategy due to concurrent moves. As a result, the LG methods lead to new ways of constructing winning strategies. LG constructs winning strategies on the basis of mathematical artifacts that LG has discovered and distilled by formalizing the strategies of experts. It is convenient to regard an LG system as a two player game where the sides (or super-agents) are the players. We will relate the notion of LG strategy for a side or a super-agent to that of a player in a two player game. Most constructions of a two player win-loss game theory are based on the concept of a game tree. This tree consists of all possible moves of players and embraces all possible plays of the game. LG attaches a state to each node (position) on the game tree. This is a state of the game, whose main content is the state of the board for the games such as chess, checkers, tic-tac-toe, etc. For the LG systems (as defined in Section 2.2) the state of the game is the state of the system. As in the game theory LG looks for strategies for both sides (players), but makes the corresponding definitions on the basis of a state of a system (or game) rather than a game tree. The focus of LG, though, is effectively computable strategies. This is in line with constructive approach to finding winning strategies in the theory of two player games as pioneered by Buchi and Landweber (1969) and continued by Gurevich and Harrington (1982), A.Yakhnis and V.Yakhnis (1990, 1993), McNaughton (1993), and Zeitman (1994). The proximity of the goals of the latter approaches to that of LG is sometimes coincidence, where LG computes a provably winning (draw) strategy for a player (Chapter 13). Some other times, LG computes a strategy for a player which is good, but it may be difficult or intractable to see whether the strategy is winning for that player. The game theory algorithms for constructing winning strategies are usually intractable due to the exponential (or worse) running time, while the LG algorithms are practical and even polynomial-time (for subclasses of problems). Slightly paraphrasing a game theory definition of a strategy for a player over a game tree, we give a definition of an LG strategy based on a game state. A strategy of a player is a partial function over game states that produces moves for that player. A winning strategy of a player is a strategy such that if the player follows that strategy two properties are satisfied. Firstly, the strategy is defined at every state at which the player has to move and which was already produced by the use of the strategy (including the Start State). Secondly, any resulting sequences of moves of both sides lead the system from the Start State to the target states for the player, while the opposing side makes arbitrary legal moves. More details about the LG strategies are provided in Chapter 13. We defined a strategy using the game tree of all possible moves of both sides. However, the LG algorithm does not generate this tree. The LG-search procedure generates a very small subtree of the full game tree by means of generating a rather small subset of all states of a system. In Section 1.4 and further in this book, this subtree is called an LG-search tree (or a reduced search tree) as opposed to the full game tree (or a brute force search tree). It is proved that for some classes of problems, the LG-search tree includes the branches that correspond to sequences of moves generated by a winning (or draw) strategy (Chapter 13). For other classes of problems, this tree includes the branches that correspond to sequences of moves generated by the best strategy known to the experts (while any winning strategy is unknown). Also, further in this book, we will write about "trees of moves", "branches (or sequences) of moves", and "variants" (virtual plays), omitting statements about one-to-one correspondence between arcs (edges) of the trees and moves of players(sides). The LG algorithm computes a strategy for a player by selecting the branches obtained by applying the minimax algorithm on the LG-search tree on behalf of both players. In practice, the tree generation and the minimax are combined in one procedure. In some cases, the LG tree is so small that all of its plays are won by the same player. In other words, this tree represents a winning strategy (Chapter 13) of that player with respect to the LG tree. It may or may not be the case that the strategy is winning with respect to the original game tree. The LG system operates by moving from one state to another. That is, a move of a player causes a transition from a current system’s state to another state. If a sequence of state transitions does not have a loop, this sequence defines a unique play on a game tree. Otherwise, there are many plays corresponding to the sequence. The plays are different only in how many times they repeat the moves that correspond to transitions in the loop(s) of the sequence of states. In other words, the plays vary in how many times they repeat the loop(s). The important fact is that the state transition system of an LG system of agents is a graph rather than a tree. However, the important decisions on whether the game terminates or who wins the game, are based on the states of the state transition system, rather than on positions in the game tree. This is due to the LG formulation of final goals of players as certain target states of the state transition system. It is important to keep in mind the distinction between the two cases of using an LG algorithm to affect the evolution of an LG system. One case is when LG strategy for a player is applied against an LG strategy for the other player. The other case is when the source of moves of the other player is not an LG strategy. In all cases the LG strategy is represented by the same LG algorithm, where the player, for which a move is sought, is an input parameter of the algorithm. Another important distinction is between moves in plays and moves in play variants or virtual plays or, simply, variants. The moves in a play constitute a sequence of moves that were actually made by players in the game. The moves in play variants are sequences of moves of both players that an LG strategy constructs in order to compute the move for the player. Such sequences of moves are possible continuations of the existing play, and they need not consist entirely or substantially of moves actually made by players. LG strategy has to rebuild the LG-search tree at each state for which it computes a move for the player. If LG strategy computes a move for the player at a state S1 and the next move at a state S2, both states will share many of the same structural components, because they are separated just by two moves: the move of the player and the move of the opponent. Thus, the LG algorithm tries to build LG-search tree for S2 by transforming that for S1. One may think that the LG strategy computes a move for a player at a system’s state S, by constructing a subset of the state transition system graph for the LG system. In fact, LG algorithm uses information about the order of moves in an essential way. The graph above represents all play variants constructed by the LG algorithm in order to select a move for the player. In reality, the LG algorithm produces an enumeration of a subset of this graph capturing the order of moves in all variants. Such an enumeration induces a subtree of the game tree extended as far as the variants went when they were computed by the LG algorithm. The subtree corresponds to playing the game beginning from the state S. Though, it is usually a very "narrow" finite subtree of the game tree corresponding to playing from S. There is one-to-one correspondence between the subtree of moves capturing all the LG variants on one hand, and the enumeration of a subset of the state transition graph according to the moves in all LG variants, on the other hand. The software system that applies LG maintains the play in the game and the game subtree representing all LG variants for the last state of the play. The LG algorithm also maintains the extensive structures (Section 1.5) associated with states that constrain the set of variants that LG computes. |
|
|
| 1.6 LG: Three Stages of Development |
|
As in physics in the 17th century, in AI and, particularly, in LG, the major generalizations and break-through are still forthcoming. However, it is quite possible that the first signs of them are around us. In this respect, it would be helpful to look back at the history of development of LG. This history may be divided into three stages. In the late 50s, in Moscow, Professor Mikhail Botvinnik, the World Chess Champion, began his investigation of the methodology of the most advanced chess players. Ten years later, this investigation resulted in the revolutionary ideas for the construction of chess programs that simulate grandmasters in playing chess. In the beginning of the 70s, Dr. Botvinnik initiated and directed research project PIONEER, with the author as key investigator. This research was conducted in Moscow at the National Research Institute for Electrical Engineering. It was funded by the USSR State Department of Science and Technology and the USSR Department of Energy. The goal of this research was to learn and implement as computer programs the methodology of the most advanced chess players as well as other domain experts for solving search problems almost without search, and, apply this approach to a wide spectrum of complex practical problems. A collection of powerful algorithms was developed within the project PIONEER (Botvinnik, 1984). Numerous experiments were performed to compare the systems based on that initial model and systems utilizing other approaches. The experiments showed that many problems, which were not solvable by the other approaches at all, were successfully solved by the prototypes of LG systems. Moreover, for the rest of the problems, the new systems were significantly faster than the other approaches. Project PIONEER continued through the end of 80s. The time period of 1958-1988 with preliminary design and vast experiments within project PIONEER is considered as the first stage of the development of LG (Section 1.7). Multiple attempts to formalize and, possibly, generalize the heuristics discovered in the course of the project PIONEER encountered enormous difficulties. These attempts began in the mid-70s pushed by the scientists who wanted other problem domains to benefit from the discoveries of this project. Another goal was to understand the fundamental nature of the results, to apply formal approach and theoretically evaluate the soundness, the completeness, and the running time of the developed algorithms. The difficulties were related to the unusual nature of the heuristic model being constructed. In particular, mathematical tools to be applied for formalization should have reflected the hierarchical and dynamic structure of the model, high flexibility of the subsystems, should have allowed global efficient control of every subsystem and the entire hierarchy. The development of the Hierarchy of Formal Languages, a mathematical model of heuristic algorithms of the project PIONEER, by the author is considered as the second stage of the LG heritage (Section 1.8). Time-wise, the first results were obtained in 1979, but the development continued through 1990 in Moscow at the National Research Institute for Electrical Engineering and later at the National Research Institute for Oil Development. This research was funded within the framework of the project PIONEER and through other sources. The year of 1990 is the beginning of the third stage of the development (Section 1.9) when LG was established as a self-determined field of research in Artificial Intelligence. This stage began at McGill University, Montreal, Canada. From September of 1991 to date, it continues at the University of Colorado at Denver, USA. In the 90s, the initial mathematical model was unified and generalized (Stilman, 1992-1998). Since both, the formal languages and the geometry of the operational district and subsystems, were involved, the advanced new model was named Linguistic Geometry in 1991. In retrospect, the previously developed part of this approach (stages one and two) is now being referred to as LG as well. The goals being pursued include the development of solid theoretical foundations, expansion to new problem domains, evaluation of complexity of classes of problems employing the LG tools and accuracy of these tools, development of efficient applications and a universal LG Testbed to be applied to a variety of problem domains. What was not expected or planned in advance is the re-development of the top-level of LG, the Language of Translations, employing the so-called no-search approach. The ability to generate provably optimal solutions for classes of problems without any tree-based search shows the fascinating power of LG that originated from expert heuristics. This investigation allowed us to identify a new class problems of low (polynomial) computational complexity among the problems that were considered computationally hard (exponential or worse). During the third stage, the funding was provided by a number of sources, including the National Science and Engineering Research Counsel (NSERC) of Canada and McGill University, Montreal, Canada, University of Colorado at Denver, USA, the U.S. Air Force Office of Scientific Research, and the U.S. Department of Energy through Sandia National Laboratories, Albuquerque, NM. It is likely that several important events taking place in 1999, including publication of this book and a substantial grant from DARPA, will assist in advancing the theory and building real world applications of LG, and manifest the beginning of a new fourth stage of the development of LG. |
|
|
| 1.7 Stage One: Project PIONEER |
|
The first ten years of research, since 1958, resulted in publication of the book "Algorithm for Playing Chess" (Botvinnik, 1968, 1970). While the mathematical formalization of the algorithm published in the book may be somewhat questionable, the major principles for search reduction laid a solid foundation for further development. Another publication entitled "A Flow-Chart of the Algorithm for Playing Chess" (Botvinnik, 1972) should be considered as an official start of the project PIONEER. Unfortunately, the above publications included nothing beyond ideas and low level flow charts. The algorithm and the program were yet to be developed. The research team involved in this project had two subjects for investigation: advanced experts (like Botvinnik himself) and computer programs, once they were developed. These programs included computer chess program PIONEER 1.x and a number of programs PIONEER 2.x - 4.x for planning and scheduling. Feedback from both resulted in constant rethinking and multiple redevelopment of both algorithms and programs. Many old and new ideas were tested in the course of the project. For example, the idea of trajectories limited by a horizon and the idea of decomposition of a complex system into the dynamic hierarchy of subsystems, proved to be essential from the very beginning. That was not the case with the second-level subsystem, the network of trajectories. Defined originally as the key area of a combat, later as a zone (in multiple versions), and as a chain of trajectories, this subsystem went through a number of major and minor changes. Heuristic algorithms for generation of the first and second-level subsystems, trajectories and Zones, were presented in (Stilman, 1975, 1977, 1984a). Similar problems were encountered with the higher-level subsystems and with the algorithm for global control later formalized as Grammar of Translations. By the end of 1976, the first version of the chess program PIONEER was completed. It was tested on solving chess endgames. Of course, the goal was not just to solve endgames. The solutions should have been obtained employing the search trees close to the trees of variants analyzed by a chess expert. With respect to accuracy, the generated solutions had never been considered as the absolute optimal solutions of the problems. Moreover, for a vast majority of the endgames, optimal solutions are still unknown. A proof of optimality employing conventional search algorithms requires enormous search and, usually, is beyond capabilities of any computers (Section 1.2). What is usually called a solution is a variant (or several variants) which experts agreed upon. A deeper understanding of optimality and its role in LG came much later in the third stage of the LG development (Section 1.9 and Chapter 13). The first two endgames selected for the program tests, R.Reti and M.Botvinnik-S.Kaminer endgames, are considered simple for a chess player. However, this simplicity is hidden behind million-move search trees to be analyzed employing the brute force approach. Of course, a chess expert is able to avoid this multitude of computations. During the experiments with PIONEER, a number of parameters evaluated included the branching factor (Section 1.2) as well as some other parameters of the search (Botvinnik, 1979, 1984). The search tree generated by PIONEER in January of 1977 while solving the R.Reti endgame contained 54 moves (T=54). Hence, taking into account that the depth of the search required here, L=6, a branching factor B≈1,68 was obtained (1.2.2). The search trees generated by conventional chess programs for this endgame include about 106 moves. In the M.Botvinnik and S.Kaminer endgame (Botvinnik, 1979, 1984), the total number of moves included in the search was equal to 145, maximum length L=12, and B≈1,35. Although both endgames are solvable by conventional chess programs, these results were very interesting because of substantial reduction of the branching factor. One of these problems, the R.Reti endgame, serves as a model for the far reaching generalizations in LG (Chapters 3, 4, 6, 13, and 14). Among the variety of complex problems solved by PIONEER, we will discuss two more. Both have yet to be solved by the conventional chess programs. The search algorithms with alpha-beta pruning (Section 1.2) failed to provide a substantial reduction of the branching factor. As a result, the expected run times were not feasible. The first problem is the G.Nadareishvili endgame (Nadareishvili, 1975, 1976; Botvinnik, 1979, 1984). It was solved by PIONEER in August of 1977. The total number of nodes generated was T=200, while the depth of the search required to find a solution is equal to 25. Consequently, B≈1,14. The unreduced branching factor might be estimated as B≈15. The solution of this endgame demonstrated power of the heuristic model, the foundation of PIONEER. A dynamic hierarchy of subsystems, trajectories and networks, allowed us to find a very deep solution almost without branching. Of course, this was just a solution approved by experts. At that time nobody raised the question of optimality or even about the accuracy of this solution. Now, 20 years later, we can suggest that this is the mathematical optimum. It is reasonable to expect that this will be proved employing ideas of the no-search approach in LG (Chapter 13) in the near future. The G.Nadareishvili endgame also served as a pattern for a number of generalizations included in this book (Chapter 5). The second complex problem is the middle-game position in the legendary game played by World Chess Champions M.Botvinnik and H.-R.Capablanca in 1938. This chess combination is usually considered as an eternal example of brilliant chess art. The start position contains 19 pieces and the unreduced branching factor might be estimated as B≈20. The depth of the search should not be less than 23. In April of 1980, program PIONEER generated a search tree of 40 nodes with the branching factor B≈1,05 (Botvinnik, 1980a, 1980b, 1982). A solution found by PIONEER was exactly the same as the variant played by the champions in 1938. It is likely that this solution is provably optimal. In 1981-1988, all the R&D on project PIONEER were supported by the software development environment called PROGRAMMER’S WORKBENCH (PW), (Stilman, 1994f). It was developed by Mirniy, Roizner, Chudakov, and Stilman (1986), and later significantly expanded by Mirniy, Chudakov, and Stilman (1988). PW was intended to support concurrent software development and configuration maintenance of large-scale research projects. PIONEER and other complex projects included an extended prototype period. Basically, the programs were used as tools for the investigation and redevelopment of algorithms. The entire software life cycle was considered as a sequence of prototypes. Each prototype should have been extremely flexible to provide multiple redesigns. PW supported multiple redevelopment iterations of changeable prototypes through the universal hard skeleton of software versions. Additionally, PW effectively supported teamwork on project PIONEER by combining independence of a software designer acting alone and strict discipline of cooperative research projects. While Dijkstra (Dijkstra, 1976; Gries, 1983; Stilman, 1994f) was the source language fully supported by PW, the actual development (including the debug mode) was conducted employing the highest-level problem-oriented language. PW allowed us to construct, expand, and maintain various versions of this language for different problem domains. PW was implemented for IBM mainframe hardware. Later, the PW tools were used at several research institutions for the development and maintenance of large-scale Artificial Intelligence projects. These tools were ready for expansion to support object-oriented frameworks. Project PIONEER resulted in the development of one of the most interesting and powerful heuristic models based on heuristic networks. Application of the developed model to the chess domain was implemented in full as program PIONEER 1.x (Botvinnik, 1979, 1982, 1984, 1989). A similar heuristic model was implemented for the long-range planning and scheduling in a number of computer programs PIONEER 2.x, 3.x, 4.x. They were used for scheduling of maintenance of power units, for smoothing the graph of power consumption, and for planning the national economy in the former USSR (Stilman, 1985a, 1993a). The models were introduced in (Stilman, 1976c, 1977, 1979, 1994a; Botvinnik, 1970, 1972, 1975, 1979, 1982, 1984, 1987, 1989), (Reznitskiy and Stilman, 1983 ; Reznitskiy, Bordiugov and Stilman, 1983), (Botvinnik et al., 1983; Botvinnik, 1989), (Stilman, 1978, 1985b, 1985c, 1993d) in the form of ideas, plausible discussions, and program implementations. Experiments with maintenance scheduling programs PIONEER 2.x demonstrated the advantages of the new approach. The program PIONEER 2.1 for monthly scheduling of power units generated various schedules with a reduced branching factor not exceeding 1,06, down from 50-100 for the brute force approach (Reznitskiy and Stilman, 1983), (Stilman, 1985a). Experiments with program PIONEER 2.2 for annual (365 days) maintenance scheduling of power equipment also demonstrated a reduced branching factor close to 1. In contrast with PIONEER 2.1, this program was able to maximize the number of power units included on the schedule by adjusting the duration of maintenance of these units. A new level of benefits was shown by the program PIONEER 2.3 that generated annual power maintenance schedules by adjusting the values of the power reserve. Slight adjustments of the power reserve (within the range of 6%) allowed this program to schedule maintenance of all the power plants that submitted requests. The most interesting results in scheduling were achieved by program PIONEER 2.4 for annual scheduling with multiple resource allocation including various types of maintenance personnel. These requirements resulted in a significant growth of the unreduced branching factor while the program managed to reduce it down to 1,005. It generated high quality annual schedules for the USSR National Power System. Application of LG to scheduling and additional details about scheduling programs are presented in Chapter 7. Programs PIONEER 3.1 and 3.2 allowed to smooth the weekly graphs of power consumption by changing weekly schedules (moving off days) for various consumers. They decreased the maximums of power consumption by 3.5% while minimizing the number of changed schedules (Botvinnik and Mirniy, 1983). The top achievement in applying PIONEER’s model in the non-chess domains was the development of the programs PIONEER 4.1 and 4.2 for planning the USSR national economy for 15 and 25 years, respectively. These programs balanced the production of the national industry and the national budget based on the aggregated 18-branch model of the national economy (Reznitskiy, 1987). The results obtained within the framework of PIONEER in solving complex search problems for various problem domains indicate that implementations of the dynamic hierarchies resulted in the construction of highly goal-driven algorithms that generated search trees with the branching factor close to one. What was in common in those hierarchies? What formal tools could be used to reflect these commonalties and to apply them in different problem domains? |
|
|
| 1.8 Stage Two: Mathematical Tools |
|
In 1979-1990, the first version of formal tools for LG was developed (Fig.1.5). A story behind this result is instructive. It was clear that the mathematical tools should have been discrete, symbolic, and should have reflected the dynamic hierarchy of subsystems. The specific requirements looked as follows. The mathematical tools should reflect the problem statement as a system of local agents, the entities, and their locations. The entities are broken down in two sides with opposing interests. They can move by changing their locations. Some of the locations are free from entities but may be occupied later. A move takes place during one time interval. All time intervals are to be equal. Also, the entities should have well-defined rules limiting their movements. A system operation can be reflected as a variant of moves. Every variant can be compared with other possible variants. A solution of a problem is the operation selected from the rest according to a certain criterion of optimality. A typical difficulty of such selection is related to the number of possible variants and, consequently, to the running time of the search required. Quite often, for real world problems, these time increased to the levels that made them practically unsolvable. The formalization of the problem statement shown above was not of great concern. This class of problems could be formally represented employing numerous existing techniques, and all representations are equivalent. However, the chosen representation of the problem statement should be well coupled with the formal representation of the method used to solve it, the LG approach. It should serve as a foundation and a mathematical environment for the formal representation of the dynamic hierarchy of subsystems. A formal problem statement (Chapter 2) was developed by following the theories of formal problem solving and planning by McCarthy and Hayes (1969), Fikes and Nilsson (1971), Sacerdoti (1975), McCarthy (1980), Nilsson (1980), and others, based on the first order predicate calculus. The main idea of this formalization of the problem statement was borrowed from the system STRIPS developed by Fikes and Nilsson (1971). |
Figure 1.5 Origin of LG: formal tools and heuristics. |
|
Even a brief description of requirements for representation of dynamic hierarchies given below shows that this task was incomparably more difficult than formalization of the problem statement. It took a number of years to come up with a satisfactory solution. A hierarchy to be introduced is intended to reveal and make use of the inherent hierarchical relationship between entities and groups of entities with respect to the main goal of a system. The lower level of the hierarchy is a trajectory, a planning path, with an entity moving along it. When it moves forward, part of a trajectory that is left behind should disappear, and re-appear again, when an entity backtracks during the search to explore another path. Formal tools should have generated all kinds of trajectories encountered in a number of problem domains, e.g., a shortest path, a path going around obstacles, etc. The higher levels of the hierarchy are networks of trajectories (with their entities). Every network has its ultimate goal related to a specific location, the final destination. A number of types of networks were introduced: attack Zones, domination Zones, retreat Zones, etc. Every network includes entities participating in achieving the ultimate goal. This participation is twofold. Entities of one side pursue their goal by moving, protecting each other, and destroying the enemies. Entities of the other side, by similar actions, do their best to prevent the opponent from achieving the goal. An entity can participate in many networks simultaneously. The movements of entities are organized in a timely fashion. For example, if an entity has enough time to move along a trajectory to intercept an opposing entity, this trajectory is included in the network and the movement is allowed. If this is not the case, the trajectory is dropped. In a network, parts of trajectories and bundles of trajectories with their entities disappear when movement along them does not make sense with respect to the ultimate goal. This may be related to the timing, the state configuration, or other reasons. Calculations of time and other factors related to the network construction and re-construction are done within each network independently. For this purpose, the other networks are ignored. Networks can be connected to each other if the ultimate goal of one of them becomes the goal of the joint network, while the goals of the components become subordinate to the main goal. In the 70s, a number of existing mathematical tools was evaluated and dropped. Usually, they did not explicitly reflect the hierarchy of subsystems or did not provide sufficient flexibility for representation of dynamic subsystems. For example, these deficiencies are inherent to the representation of trajectories and networks as graphs. At that point, a linguistic representation was considered as a candidate. Indeed, a trajectory is a finite sequence of planning steps of an entity while a string is a finite sequence of symbols. It seems reasonable to represent trajectories as formal strings of symbols. In this case, a set of trajectories could be represented as a formal language. The next question to be answered was how to represent the hierarchies via languages. It was quite a surprise when we realized that the linguistic representation of hierarchies is most natural. Indeed, a set of dynamic subsystems could be represented as a hierarchy of formal languages where each sentence, a group of words (a string of symbols), of the lower level language corresponds to a word in the higher level one. This is a routine procedure in our natural language. For example, the phrase: "A man who teaches students" introduces the hierarchy of languages. Symbols of the lower-level language may include all the English words except "professor". A higher-level language might be the same language with addition of one extra word "professor" which is simply a short designation for "A-man-who-teaches-students". Note that the hierarchical architecture of natural languages and related approaches adopted in LG are examples of the general semiotic mechanism of multiresolution introduced later by Meystel (1996a, 1996b). The key question remained: what are the specific languages to be used for the model? In the 50s through 70s, a formal syntactic approach to the investigation of properties of natural language resulted in the fast development of the theory of formal languages by Chomsky (1963), Ginsburg (1966), Hopcroft and Ullman (1979), and others. This development provided an interesting opportunity for dissemination of this approach to different areas. In particular, there came an idea of analogous linguistic representation of physical images (Fig.1.5). This idea was successfully developed into syntactic methods of pattern recognition by Narasimhan (1966), Fu (1974, 1982) and Pavlidis (1977), and picture description languages by Shaw (1969), Feder (1971) and Rosenfeld (1979). The Plex languages introduced by Feder (1971) demonstrated a particular descriptive power. In a usual string of symbols, every symbol is connected only with two neighbors, left and right. It has two attaching points. In Plex languages, a symbol called NAPE (an n Attaching-Point Entity) can have an arbitrary number n of attaching points for joining to other symbols. The resulting strings represent general higher-dimensional patterns that allow us to generate images that represent trees, sophisticated chemical formulas, electrical circuits, etc. Something similar could be done in LG with trajectories and networks. Searching for adequate mathematical tools formalizing heuristics, we transformed the idea of linguistic representation of complex natural and artificial images into the idea of similar representation of complex hierarchical systems (Stilman, 1981, 1984b, 1985a, 1985b, 1985c, 1992). However, the appropriate languages should have had more sophisticated and flexible attributes than languages usually used for pattern description. Origin of such languages can be traced back to research on programmed attribute grammars by Knuth (1968), Rozenkrantz (1969) and others. In this respect, special attention should be paid to the results of N.Volchenkov (1979) and L.Kuzin (1979). Volchenkov developed incredibly powerful generating grammars, which he called BUPPG. A modification and generalization of these grammars (Stilman, 1993a, 1993b) allowed us to generate languages that met all the requirements for representation of dynamic hierarchies. This modification, named controlled grammars (Chapter 8), allowed us to use them as a universal tool on all levels of LG and formally prove correctness and completeness of the generated languages, and evaluate their running time (Chapters 8-12, and 14). A new version of controlled grammars is considered in (Yakhnis V., Yakhnis A. and Stilman B., 1996, 1997). Until the third stage of LG development, in the beginning of the 90s, the formal tools were not organized as a full-scale complete mathematical model. Development of the programs PIONEER at the second stage was based on a collection of heuristic algorithms. Multiple experiments with these programs allowed us to make far reaching generalizations and later construct a mathematical model. |
|
|
| 1.9 Stage Three: Modern History |
|
Since 1991, this approach is called Linguistic Geometry (LG), due to the geometrical nature of the discovered heuristics and the mathematical tools of the theory of formal languages used to formalize them. A complete presentation of the two levels of the hierarchy of languages was given in (Stilman, 1993a, 1993b, and 1994d). In the 70s and 80s, the goals of research were related to the discovery of the most intimate features of expert search heuristics and the development of draft formal tools in order to formalize them. In the 90s, with the establishment of LG, the goals have changed. In the third stage of LG development, the scientific goals are related to the exploration of the limits of efficiency, generality, computational complexity, and accuracy of LG. A partial list of questions for the research on LG in the 90s is as follows. What is going to be the most efficient general structure of the LG applications? Are the higher-dimensional problems really solvable employing LG tools? What would be the impact on the running time if we switch from 2D to 3D problems? How would the running time change if we increase the number of agents and provide them with more advanced moving abilities? Can we solve problems with partially or even totally concurrent moves employing similar formal tools? What is the computational complexity of these problems? Fortunately, and unexpectedly, not only these, but the following additional questions were answered as well. How accurate are the solutions? Can we evaluate and prove a certain level of accuracy? If our proof is constructive, how can we use the same techniques for generating solutions? All the programs developed in the 70’s and 80’s within the framework of the project PIONEER were highly problem oriented. They served as implementations of heuristic hierarchies of subsystems for specific problem domains. In the 90s, we began exploration of various software tools and approaches for the implementation of the general hierarchy of formal languages and their applications. A set of general LG grammars was first implemented at the University of Colorado at Denver in 1993 by D.King and R.Mathews employing CLIPS and C languages, respectively (King, 1993), (Mathews, 1993). While R.Mathews implemented just two levels of the hierarchy, trajectories and Zones, D.King developed a working prototype of the full scale hierarchy of grammars using the CLIPS programming environment. Also, he showed that CLIPS programming tools (Giarratano and Riley, 1998), intended originally for the expert system’s development, demonstrated high efficiency for the quick implementation of the LG grammars. Of course, efficiency at the implementation stage was achieved at the expense of the running time of the application. However, these tools could serve as a platform for the development of prototype versions. Another direction of research was related to exploration of actual applicability of the general LG tools to various problem domains. In 1995, C.Fletcher implemented the Grammars of shortest and admissible trajectories with generalized relations of reachability employing C++ (Fletcher, 1996), (Fletcher and Stilman, 1997). He applied this tool for the development of the simulation software prototype of robot control in industrial environment. Interpretation of various robot movements via relations of reachability allowed this system to make sub-optimal path planning for robots and avoid collisions with immobile and mobile obstacles. Various versions of this prototype were demonstrated at Sandia National Laboratories, Rockwell Science Center, and at a number of conferences. A domain-oriented version of the LG tools was developed by R.Turek (Turek, 1996 and 1997). He developed highly efficient commercial software for the real-time emergency vehicles’ routing. These vehicles (police, fire, and ambulance) were directed to the place of emergency in response to the 911 phone call. The LG grammars used relations of reachability that reflected traffic impedance on the streets of the city of Aurora, CO. The street maps were retrieved from the geographical information system (GIS), while information about impedance was updated in sub-real time employing information collected by cruising police vehicles. Prototypes of this program were demonstrated at the NASA Goddard Space Flight Center at Greenbelt, MD, and at a number of conferences. In 1996, D.Wood developed BGF, a universal framework for board game applets, employing Java (Wood, 1996). This tool was intended for the development of advanced interfaces of the LG applications for various problem domains. In 1997-98, the BGF was used by E.Skhisov for the development of his combat simulation tool (Skhisov, 1997). Combat simulation tool, the most advanced implementation of the LG algorithms so far, was developed by E.Skhisov in 1997 within the joint project of the University of Colorado at Denver and the University of Denver (Skhisov, 1997), (Skhisov and B.Stilman, 1997, 1998a, and 1998b). His tool generated the full scale hierarchy of languages including a prototype version of the Grammar of Translations, the no-search approach (Chapter 13). This implementation was intended for exploration of novel concepts in LG. In particular, this was the first tool applicable to the problems with concurrent movements of agents. Also, this was the first implementation of LG for the parallel computing environment, a network of computers. Specifically, the Grammar of Trajectories was executed in parallel. Combat simulation tool was implemented in C++ and Java. A new version of the tool is being developed exclusively in Java. In 1998, the class of problems in which LG is applicable was expanded by inclusion of the problems for the local agents that move with variable speed. This expansion makes the LG models closer to the real world problems. M.Stilman generalized the relations of reachability and modified the Grammar of shortest trajectories for this case (M.Stilman and V.Yakhnis, 1998), (DEF 2.4 and Section 9.10). His C++ implementation of this grammar generated all the shortest paths for an airplane which must avoid flying over certain territories. At the beginning the airplane accelerates, then it courses with a constant speed, and, in the end of the flight, it slows down to land. Application of LG to the Safety Critical Control Systems, Cruise Missiles Control, Planetary Exploration Vehicles, National Missile Defense (with threat and countermeasure assessments), and Space Combat are currently being considered. As the general structure and details of the LG implementations become clear, a new project is being considered. A universal LG Testbed will serve as a framework for the development of LG applications by tuning to the specific problem domain. Also, this Testbed will be used for quick testing of new ideas and concepts in LG. To answer the questions about the limits of applicability and resource requirements of the LG solutions, we developed a number of problems of gradually increased complexity. Some of them were based on the endgames considered in the past, R.Reti endgame, G.Nadareishvili endgame, and others. The sequence of problems of gradually increased complexity included problems with 3D and n×n district, greater number of agents, sophisticated mobility, alternating concurrent and totally concurrent movements, etc. Solving these problems with the LG tools should give us a basis for further theoretical investigation. In 1993, the CLIPS-based implementation of the hierarchy of grammars was applied to the problem of optimal control of four robotic vehicles in a 2D space participating in a two-player game. The problem was represented as 2D 4-agent discrete pursuit-evasion game, the 2D/4A problem (Stilman, 1996a, 1997a, and Chapter 3), a version the R.Reti endgame. Conventional approaches require a million move tree to solve it. The LG tools allowed us to find the solution by generating the search tree which included only 46 moves, with the branching factor of 1,65. An interesting result was obtained in 1994, when the 2D/4A problem was generalized for the 3D case, the 3D/4A problem (Stilman, 1994b, 1994c, 1996a, and Chapter 4). The problem was represented as a pursuit-evasion game of space stations that have to reach designated areas in space, and space ships that may intercept stations or prevent interception. The conventional approaches require a trillion move tree to solve it, while the tree generated by the LG tools consisted of merely about 50 moves with the branching factor close to one. Apparently, the LG tools allowed us to eliminate the exponential growth of the running time (with respect to the input) for this class of problems (Section 4.4). Another significant test of the LG tools, involving much larger state space, was conducted for the 2D and 3D pursuit-evasion games, which involve 8 aerospace vehicles with advanced moving abilities (Stilman, 1995a, 1995b, 1997d, and Chapter 5). This was a version of G.Nadareishvili endgame. The depth of the solution and, therefore, the depth of the search, was extremely big, at least 25 moves. Theoretical estimates showed that finding solutions of these problems requires generation of search trees that include approximately 1525 and 3025 moves for the 2D/8A and 3D/8A problems, respectively. To generate a tree of that size is beyond reasonable time constraints of any computer. In contrast, the search trees generated employing the LG tools consist of about 150 moves. The branching factor was just 1,12. These examples demonstrated significant growth of complexity: the number of vehicles, their moving abilities, the dimension of an operational district, and, especially, the required depth of the search. While the running time of the analysis-of-a-state increased, we can suggest that this is just a low-degree polynomial growth with respect to the length of the input. (The evaluation of the running time is presented in Chapter 14.) The search trees practically did not grow. In all the experiments, the search trees were very small, which allows us to suggest that the size of these trees is also a low-degree polynomial with respect to the input. We can conclude that the total computational requirements of the LG models, which is a product of the running time of the analysis-of-a-state procedure and the size of a tree, is a polynomial. In the above examples, the mobile entities, aircraft, spacecraft, etc., moved in a serial mode, one entity at a time. Moreover, the movements of the opposing sides alternated. It was desirable to expand the LG approach to the problems with concurrent movements. A formal definition of the class of multiagent systems, where LG is applicable, never included the requirement of serial or alternating moves, however, all the examples included the serial moves only. A new direction for application of LG to multiagent systems with high degree of concurrency was established in 1994 (Stilman, 1995c, 1995d, 1997a, 1997b, and Chapter 6). A new class of games, called multiagent graph-games with simultaneous moves, was developed by V.Yakhnis, and the author (1995). These new games permit simultaneous (concurrent) moves of several cooperating/competing agents; moreover, each super-agent may either skip or move one or more local agents at the same time. A number of examples were developed in 1994-95. We gradually increased the level of concurrency while trying to explore its impact on the effectiveness of the LG tools (Chapter 6). Application of LG to the problems with totally concurrent movements was initially funded by the U.S. Air Force within the Summer 1995 Faculty Associateship Program at Phillips Laboratory, Kirtland AFB (Stilman, 1997a). A prototype of the program for the real time generation of the air combat scenario was developed at Phillips Laboratory in 1995. It was intended to control manned and unmanned aerial vehicles guided by the satellite based sensors to detect mobile adversarial missile launchers and destroy them. In 1996, this research was supported by a grant from the Sandia National Laboratories. In these problems, the aircraft, both cooperating and opposing, could move concurrently. These applications involved two opposing teams, two aircraft on each team. Introduction of concurrency resulted in a significant growth of the branching factor - if we apply the brute force search - up to 324. This is the base of the exponent that shows the size of the search trees to be generated. In contrast, the search tree generated by the LG tools for this totally concurrent model contains just 40 moves with the branching factor of about 1,5. Later, these results were generalized for an n×n district, (Stilman and Fletcher, 1998, and Chapters 6, 13, and 14). While introduction of concurrency has a profound impact on the running time of conventional algorithms, it appears not to be the case with the LG solutions. Apparently, this means that the LG tools allowed us to identify a subclass of low (polynomial) complexity problems in the class of problems that are usually considered as computationally hard. This subclass includes not only serial but concurrent problems as well (Chapters 13 and 14). A deeper investigation of these issues is forthcoming. One of the latest achievements in LG is the mathematical proof of optimality of the solutions obtained for some classes of problems, including the so-called Reti-like combat simulation problems (Stilman, 1996b, 1997c, 1997d). This investigation was supported by a grant from the Sandia National Laboratories. This result, obtained in 1996 and later improved, still looks amazing for those involved in research on LG. During the entire history of the development of LG, the major concern was how to demonstrate the quality of the approximate solutions, almost winning strategies, e.g., how to measure their accuracy. As it was discussed earlier, these were solutions approved by experts. Existence of an error was not even in question because heuristic algorithms usually do not guarantee optimum. For years we have tried to come up with a measure of this error. Surprisingly, this research resulted in a proof of no error for the Reti-like problems (Section 13.9). This new result tells us that the LG tools generate optimal solutions for a class of search problems. Optimality means that the result is the same as the solution, which could be obtained using the exhaustive search. The most interesting feature of this proof is that it is constructive. The proof is based on a decomposition of the State Space into subsets of states and a construction of the set of paths between these subsets. Every path represents an intend-to-win LG strategy for one of the super-agents. This set of paths is the full set of strategy-candidates. Then some of the candidates are pruned as non-implementable. An attempt of implementation of the rest of the strategy-candidates, the best left for each side, will result in the actual construction of the solution, the (optimal) strategy for this problem. Two solutions, the one constructed in the proof, and the original generated by the LG tools, are the same. However, the new solution, obtained by construction of strategies, does not use any tree-based search. Moreover, it is provably optimal. It was desirable to convert this proof into the pure construction of solutions. This was accomplished in 1998 (Stilman, 1998a, 1998b, and Chapter 13). It was named a no-search approach. This approach was expanded to problems with concurrent movements of agents. A combat simulation tool developed by E.Skhisov was used first for experiments with concurrent problems employing the no-search approach (Skhisov and Stilman, 1998a and 1998b). The problems were solved with the branching factor equal exactly to one, i.e., without branching to different directions. At the moment, we have two versions of the top level of the LG algorithm, the Grammar of Translations and the no-search algorithm. The former is a universal tool applicable to various problems. However, it generates a search tree, though small, and does not provide a formal basis for a conclusion about the accuracy of the solution; usually, it generates best known solutions. On the other hand, the no-search algorithm generates a provably optimal solution, a winning strategy, without any tree-based search, but at the moment it is only applicable to a subclass of problems. Note that the term "no-search approach" means that the tree-based search has been eliminated, but the algorithm may still include some other types of searches, e.g., polynomial-time searches. It is likely that the future research based on the expansion of the no-search approach will cause redevelopment of the top level of hierarchy of languages, the Language of Translations. Besides the problems with mobile entities and opposing sides (such as robot simulation), the LG tools can be effectively applied to the problems without explicit conflict and opposing sides, e.g., to scheduling problems with resource allocation. The foundations of this approach are related to applications of project PIONEER to scheduling and planning at the Stage One of LG development (Section 1.7). To apply the LG tools, we introduce an artificial two-player game, i.e., artificial conflict, operational district, mobile entities, and opposing agents (Stilman and Fletcher, 1998, and Chapter 7). This formulation allows us to solve a number of problems of much higher dimension, which are intractable employing conventional approaches. Stilman Boris, (2000). "Linguistic Geometry: From Search to Construction", Series: Operations Research/Computer Science Interfaces Series, Vol. 13, 2000, 416p., Hardcover, ISBN: 0-7923-7738-9, © Springer. Part of Springer Science+Business Media |
|
▲ Top page ▲ Table of Contents |
|
Date update 09.09.2005, size=189 359 bytes
© 2004, Alexander Timopheyev, Kharkov, Ukraine, About eMail: atimopheyev@yahoo.com |