|
◄ Глава 1.7
▲ Выше
Глава 1.9 ►
|
| 1.8 Этап 2: Математические Инструменты |
|
В 1979-1990 годах была разработана первая версия формальных инструментов для LG (рис.1.5). История получения этих результатов — поучительна. Было ясно, что математические инструменты должны быть дискретными, символическими и должны отражать динамическую иерархию подсистем. Более точно эти требования описаны ниже. Математические инструменты должны отражать постановку задачи как системы локальных агентов и их местоположений. Агенты разделяются на две стороны с противоположными интересами. Агенты могут перемещаться, изменяя свои местоположения — пункты. Некоторые из пунктов остаются свободными от агентов, но могут быть заняты ими позже. Ход делается в течение одного временного интервала. Все интервалы должны быть равны по времени. Также, агенты должны иметь чёткие правила, ограничивающие их движения. Функционирование системы можно представить как вариант, состоящий из последовательности ходов. Каждый вариант может сравниваться с другими возможными вариантами. Решение задачи — это вариант, выбранный среди всех по некоторому критерию оптимальности. Типичная трудность такого выбора связана с числом возможных вариантов и, следовательно, с продолжительностью требуемого перебора. Весьма часто, для задач из реальной жизни, время перебора возрастает так сильно, что они становятся практически неразрешимыми. Формализация постановки задачи в том виде, как она описана выше, не представляла трудности. Этот класс задач мог быть формально представлен с использованием многочисленных уже существующих методов, причём все они эквивалентны. Однако, важно, чтобы выбранное формальное представление постановки для класса задач соответствовало формальному представлению метода, который использовался при решении этих задач, т.е. LG-подходу. Это представление должно было стать основой и математической средой для формального представления динамической иерархии подсистем. Формальная постановка задачи (глава 2) была разработана, следуя известным теориям формального решения задач и планирования, разработанным в статьях (Маккарти и Хайеса, 1969; Файкса и Нильсона, 1971; Сакердоти, 1975; Маккарти, 1980; Нильсона, 1980 и в других), которые основаны на исчислении предикатов 1-го порядка. Основная идея этой формализации была заимствована из системы STRIPS, разработанной Файксом и Нильсоном (1971). |
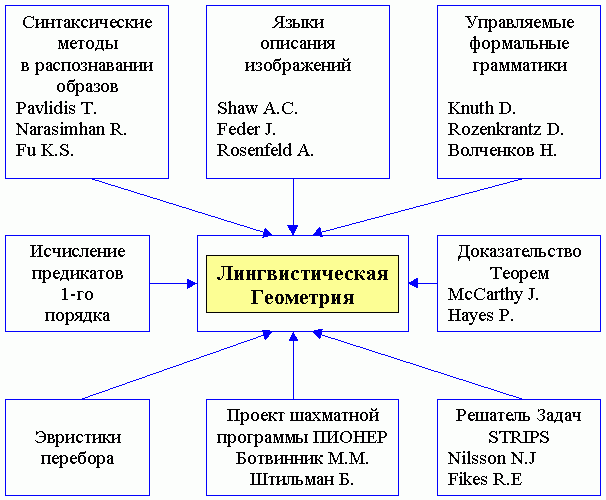
Рис.1.5 Происхождение LG: формальные инструменты и эвристики. |
|
Даже краткое описание требований для представления динамических иерархий, приведенное ниже, показывает, что проблема формализации этого представления была несравнимо труднее, чем формализация самой постановки задачи. Прошли годы, прежде чем удовлетворительное решение было получено. Иерархия, которую следовало ввести, должна была проявить и отразить ту глубокую иерархию взаимоотношений, которая возникает между агентами и группами агентов, при их стремлении к главной цели системы. Низший уровень иерархии — это Траектория, т.е. планируемый путь вместе с агентом, движущимся по этому пути. Когда агент продвигается, то пройденная часть траектории должна исчезнуть и вновь появиться при возврате агента в процессе перебора (когда агент "пятится"), чтобы исследовать другой путь. Формальные инструменты должны генерировать все виды траекторий для разных проблемных областей, например, самый короткий путь, путь для обхода препятствий и т.д. Более высокие уровни иерархии — это Сети Траекторий (вместе с их агентами). Каждая Сеть Траекторий должна иметь конечную цель с определенным местоположением, т.е. конечным пунктом назначения. Множество сетей должно включать Зоны нападения, Зоны доминирования, Зоны отступления и т.д. Каждая сеть должна включать агентов, участвующих в достижении конечной цели. Это участие является двойным. Агенты одной стороны преследуют свою цель, перемещаясь, защищая друг друга и уничтожая врагов. Агенты другой стороны подобными же действиями стараются препятствовать противнику в достижении его цели. Агент может участвовать во многих сетях одновременно. Движения агентов организованы с учётом времени. Например, если агент имеет достаточно времени, чтобы пройти по траектории и перехватить агента противоположной стороны, то эта траектория включается в сеть и движение по ней разрешается. Если дело обстоит не так, то траектория отбрасывается. При перемещении агентов в другие пункты часть траекторий и пучков траекторий сети застывает, когда движение агентов по ним уже не имеет смысла относительно конечной цели. Это может быть связано с недостатком времени, конфигурацией состояния (позицией) или с другими причинами. Вычисление времени и других параметров, связанных с построением и реконструкцией сети, производится для каждой сети независимо друг от друга. Связи с другими сетями при этом игнорируются. Сети могут быть связаны друг с другом, если конечная цель одной из них становится главной целью объединенной сети, тогда цели других сетей-компонентов подчиняются главной цели. В 70-х годах многие из известных математических инструментов были пересмотрены и отброшены. Обычно, они не отражали явно иерархию подсистем или не обеспечивали достаточную гибкость для представления их динамичности. Например, эти недостатки свойственны представлению траекторий и сетей в виде графов. В этой связи лингвистическое представление также рассматривалось в качестве кандидата. Действительно, траектория — это конечная последовательность запланированных ходов агента, в то время как слово — это конечная последовательность символов. Кажется, разумным представить траектории как формальные слова, составленные из символов. В этом случае множество траекторий можно представить как формальный язык. Но как с помощью языков представить иерархии? К нашему удивлению мы поняли, что лингвистическое представление иерархий является и наиболее естественным. Действительно, множество динамических подсистем можно представить как иерархию формальных языков, в которой каждое предложение — группа слов языка более низкого уровня — соответствует слову в высокоуровневом языке. Это стандартная процедура на нашем естественном языке. Например, фраза: "Человек, который преподаёт студентам", вводит иерархию языков. Символы языка низкого уровня могут включать все слова кроме слова "профессор". Высокоуровневый язык мог бы быть тем же самым языком, но дополненным ещё одним словом "профессор", которое является просто кратким обозначением для фразы "человек, который преподаёт студентам". Следует отметить, что иерархическая архитектура естественных языков и аналогичный подход, принятый в LG, — это примеры общего семиотического механизма мультирезолюций (иерархии моделей разного разрешения), введенного позже А.Майстелом (Майстел, 1996a, 1996b). Оставался ключевой вопрос о том, какие языки следует использовать для этой модели? В течение 50-70-х годов, формально-синтаксический подход к исследованию свойств естественного языка привёл к быстрому развитию теории формальных языков (Хомский, 1963; Гинсбург, 1966; Хопкрофт и Ульман, 1979 и другие). Это развитие предоставило интересную возможность для распространения лингвистического подхода в другие области. В частности, возникла идея об аналогичном лингвистическом представлении физических образов (рис.1.5). Эта идея была успешно разработана и воплощена в синтаксических методах распознавания образов (Нарасимхан, 1966; Фу, 1974, 1982; Павлидис, 1977) и языках описания изображений (Шоу, 1969; Федер, 1971; Розенфельд, 1979). Плекс-языки, введеные в (Федер, 1971), продемонстрировали значительную описательную мощь. В обычной строке символов каждый символ связан только с двумя соседями — левым и правым. Поэтому он имеет две точки сцепления. В Плекс-языке символ называется NAPE (n Attaching-Point Entity, т.е. n-связанный объект) и может иметь произвольное число n-точек сцепления для соединения с другими символами. Результирующие слова представляют общие многомерные образы, которые позволяют генерировать образы, представляющие деревья, сложные химические формулы, электрические схемы и т.д. Нечто аналогичное можно было бы сделать в LG с Траекториями и Сетями. В поисках адекватных математических инструментов, формализующих эвристику, мы преобразовали идею лингвистического представления сложных естественных и искусственных образов в идею аналогичного представления сложных иерархических систем (Штильман, 1981, 1984b, 1985a, 1985b, 1985c, 1992). Однако соответствующие языки должны были бы иметь более изощрённые и гибкие атрибуты, чем языки, обычно используемые для описания образов. Происхождение таких формальных языков можно проследить ретроспективно, начиная с исследований программируемых и атрибутных грамматик (Кнут, 1968; Розенкранц, 1969 и прочие). В этом отношении, особого внимания заслуживают результаты Н.Волченкова (1979) и Л.Кузина (1979). Волченков разработал исключительно мощные порождающие (генерирующие) грамматики, которые он называет БУППГ. Модификация и обобщение этих грамматик (Штильман, 1993a, 1993b) позволили нам построить языки, которые удовлетворяли всем требованиям для представления динамических иерархий. Эта модификация, названная управляемыми грамматиками (глава 8), позволила использовать их как универсальный инструмент на всех уровнях LG, формально доказывать правильность и полноту построенных языков, оценивать вычислительную сложность их порождения (главы 8-12 и 14). Новая версия управляемых грамматик рассмотрена в (В.Яхнис, А.Яхнис и Б.Штильман, 1996, 1997). До третьего этапа развития LG, в начале 90-х годов, формальные инструменты ещё не были организованы в полномасштабную математическую модель. Развитие программ ПИОНЕР на втором этапе было основано на наборе эвристических алгоритмов. Многократные эксперименты с этими программами позволили сделать далеко идущие обобщения и позднее построить математическую модель. |
|
◄ Глава 1.7 ▲ В начало текущей Глава 1.9 ► |
|
Последнее обновление 09.09.2005, size=16 590 bytes
© 2005 г., Александр Тимофеев, г.Харьков, Украина, Об авторе eMail: atimopheyev@yahoo.com |